1. 단순회귀모형
회귀모형 (Regression Model)
- 현상의 결과에 영향을 주는 복수의 요인을 연결하는 모형
- 목적변수 y에 대해, 이를 설명할 것으로 생각되는 복수의 설명변수
- x = (x1, ... , xp)T 와의 관계를 나타내는 모형


모델링 (Modeling)
- 모형 구축을 위한 일련의 프로세스
- 현상이 투영되어 있는 데이터에 기초에 모형을 상정
- 추정된 모형을 평가하고 선택
회귀모형의 종류
1. 선형회귀모형 (Leinearizable Regression Model)
- 단순회귀모형 : 목적변수 y의 변화를 적절히 파악한다.
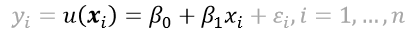
- 중회귀모형 : 최적의 설명변수의 조합을 선택한다.
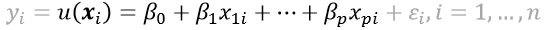
- 다항회귀모형 : 차수(p)를 선택한다.
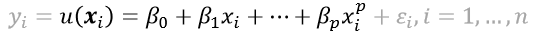
2. 비선형회귀모형 (Non-Linear Regression Model)
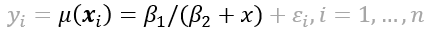
📌 선형과 비선형의 판단기준
설명변수에 대한 선형함수인가 비선형함수인가? (X)
회귀계수 β의 선형함수인가 비선형함수인가? (O)
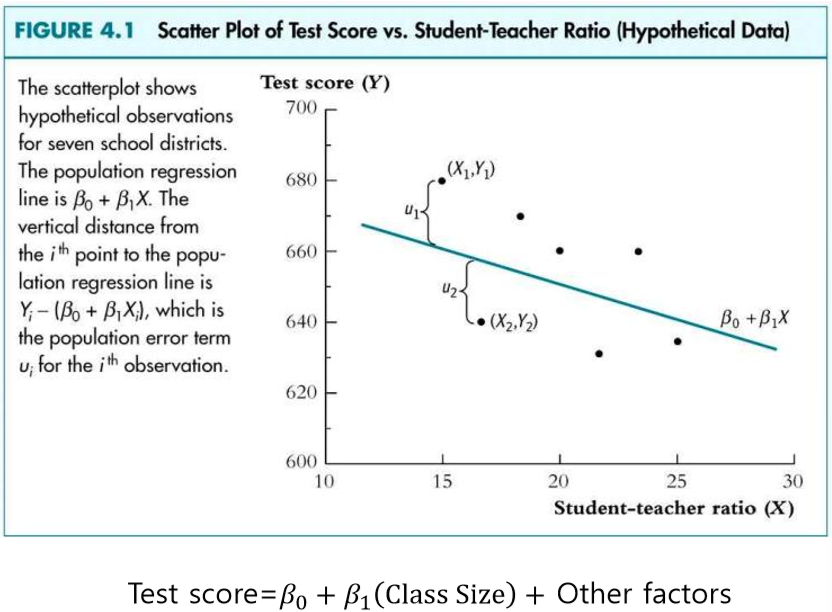
단순회귀모형 예제
교사를 채용한다면 교사 당 학생수가 줄어들어 개별 학습을 받을 수 있지만 인건비가 증가한다는 부담이 있다.
"학습의 크기를 줄이는 것이 학생의 수학능력에 어떤 효과를 미치는지" 를 알아보고자 한다.

2. 회귀계수 추정
선형회귀 모형의 성질

※ 추가 설명
1. 는 확률변수이다. 이때 확률변수가 되는 이유는 오차항 이 확률변수이기 때문이며
"상수항 + 확률변수 = 확률변수 " 이다.
2. 평균은 곧 기대값을 의미한다. 우리는 가 오차없이 정확한 값임을 기대하기 때문에 오차항이 제외된 항이 의 기대값의 정의가 된다.
3. 분산은 곧 값이 변동하는 정도를 의미한다. 는 상수항+오차항 으로 구성되어 있다. 따라서, 변동하는 부분은 오차항이므로 가 의 분산이다.
4. 와 그 자신의 공분산은 곧 오차항끼리의 분산이다. 오차항들은 서로 독립이기 때문에 공분산이 0이다.
최소제곱 추정법 (Least Square Estimation Method)
오차제곱합을 최소화 하는 직선을 찾는다.
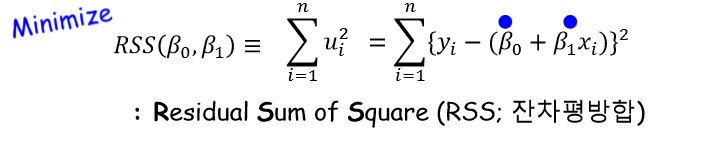
최소제곱 추정량
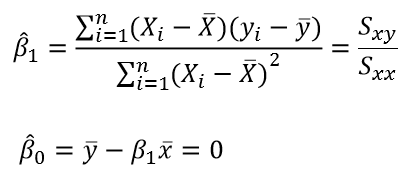
💡 질문과 피드백 사항은 댓글에 편하게 남겨주시기 바랍니다.
❤️ 도움이 되셨다면 공감 부탁드립니다.
