주제: 머신러닝 회귀, 분류 평가지표

파이썬 머신러닝 완벽 가이드[개정2판] pp.116-126 참고해서 내용 작성하였습니다.

---

1. 회귀 평가지표

• 실제값과 예측값의 차이가 작을수록 해당 모델의 성능이 좋다는 것을 의미함.

---

1.1. MSE (평균 제곱 오차)

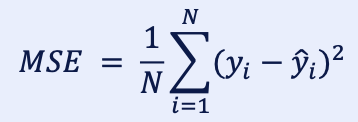
• Mean Squared Error로 평균제곱오차를 의미

• 실제값과 예측값의 차이를 제곱하여 평균한 것

장점

• 오차의 민감도를 높였고, 잔차의 값이 음수가 될 수 있는 경우를 방지함.

단점

• 예측 변수와 단위가 다르고 잔차를 제곱하기 때문에 이상치에 민감함.

---

1.2. RMSE (평균 제곱근 오차)

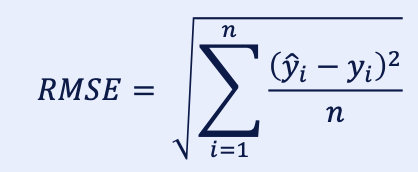
• Root Mean Squared Error로 평균 제곱근 오차를 의미함.

• MSE에 루트 씌움

장점

• 직관적이고 예측변수와 단위가 같음.

• 제곱 값을 루트로 풀어주기 때문에 잔차를 제곱해서 생기는 값의 왜곡이 덜함.

단점

• 실제 값에 대해 understimates인지 overstimates인지 파악 어려움.

---

1.3. MAE (평균 절대 오차)

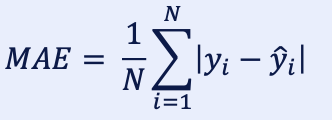
• Mean Absolute Error로 평균 절대 오차를 의미함.

• 실제값과 예측값의 차이를 절댓값으로 변환해서 평균함.

장점

• 잔차의 값이 음수가 될 수 있는 경우를 방지함.

• 예측변수와 단위가 같음.

단점

• 잔차에 절대값을 씌우기 때문에 실제 값에 대해 uderstimates인지 overstimates인지 파악 어려움.

---

1.4. MAPE (평균 절대 비율 오차)

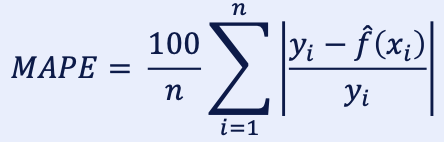
• Mean Absolute Percentage Error로 평균 절대 비율 오차를 의미함.

• MAE를 비율로 표현한 것

장점

• 직관적임.

• 비율 변수이기 때문에 다른 평가지표에 비해 비교 용이함.

단점

• 실제값에 대해 understimates인지 overstimates인지 파악 어려움.

---

2. 분류 평가지표

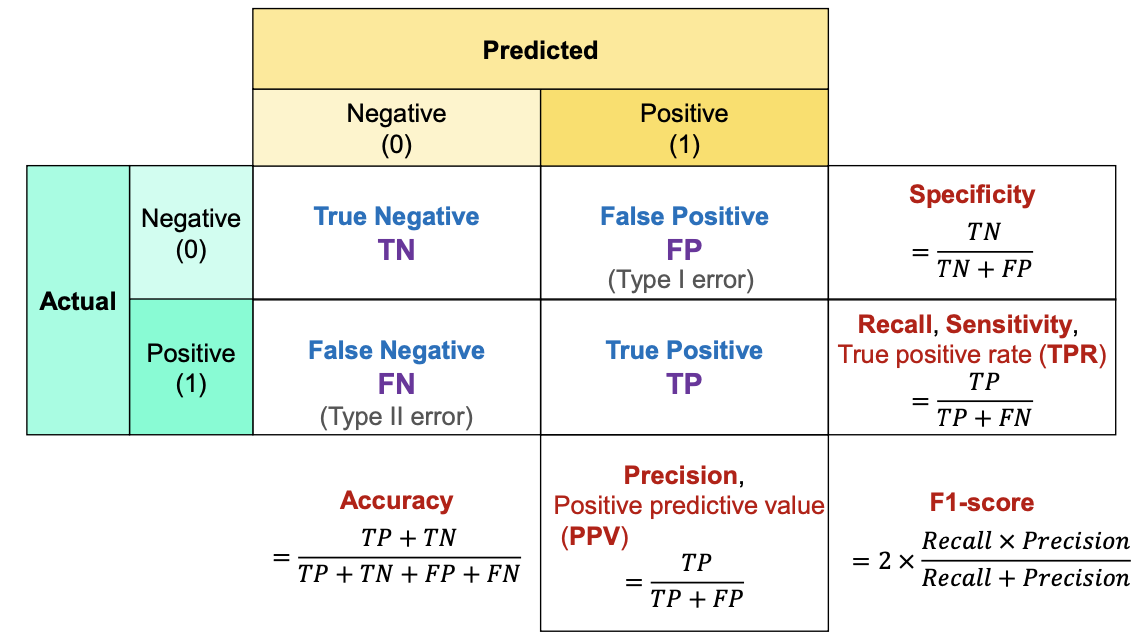
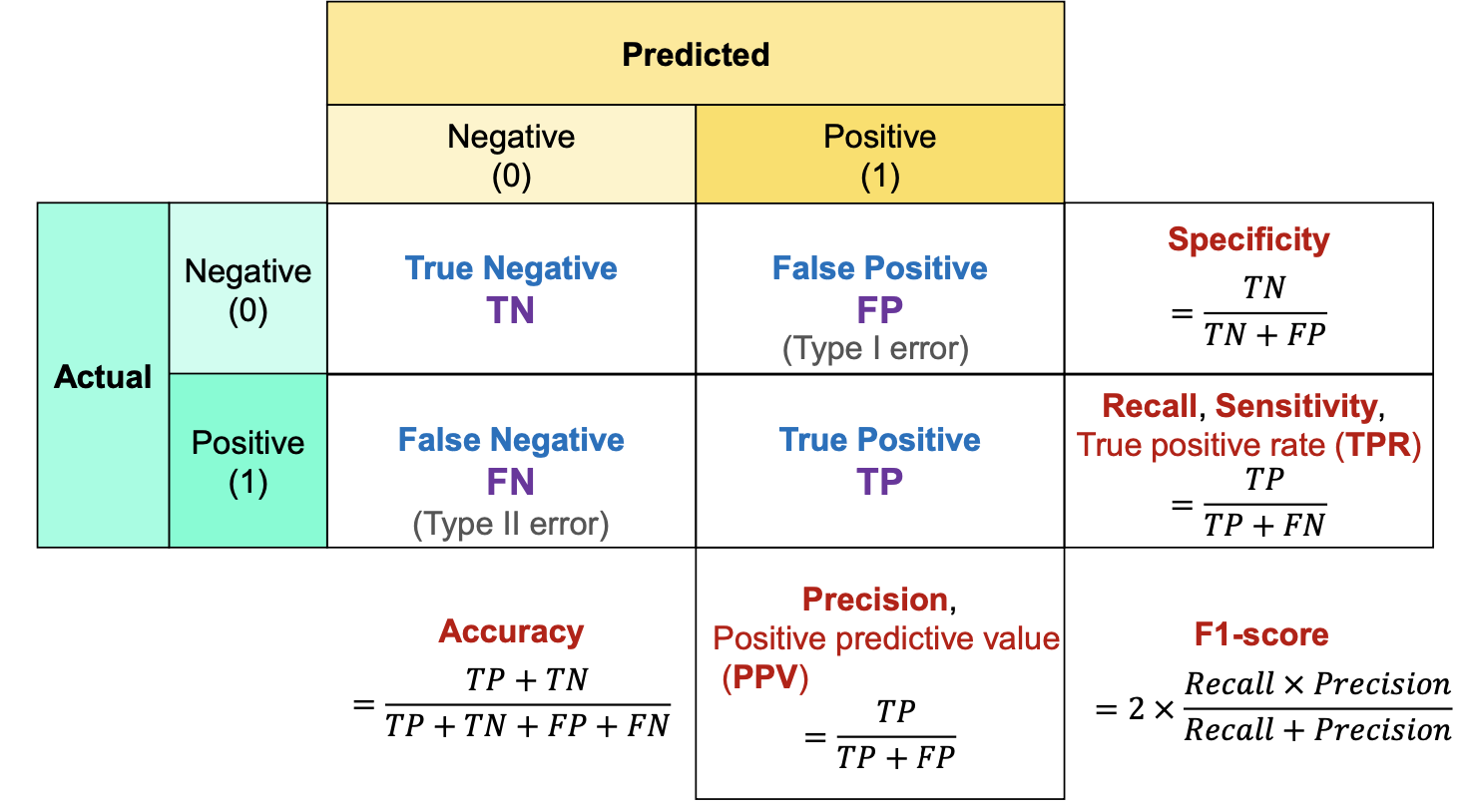
2.1. Confusion Matrix (오차행렬)

출처

• 분류 평가지표로 실제값과 예측값이 일치하는 수가 많을수록 모델의 성능이 좋은 것을 의미함.

• 실제 정답에 대한 모델 예측을 표 형식으로 시가고하한 행렬로 예측의 성능을 측정하기 위해 예측과 실제 정답을 비교하기 위한 표임.

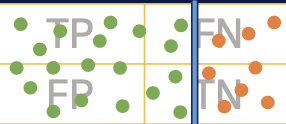
1. True Positive(TP)

• 실제 True를 True라고 예측

2. False Positive(FP)

• 실제 False를 True라고 예측

3. False Negative(FN)

• 실제 True를 False라고 예측

4. True Negative(TN)

• 실제 False를 False라고 예측

2.1.1. 정확도 (Accuracy)

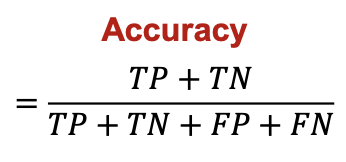
• 분류 문제에서 가장 많이 사용되는 성능 지표

• 전체 데이터 중 정확하게 예측한 데이터의 비율

---

2.1.2. 특이도 (Specificity)

• 의학분야에서 주로 사용하며, 정상인 사람을 실제 정상이라고 분류하는 비율

• Negative로 예측한 것 중, 진짜 Negative의 비율

• Negative에 집중한 평가지표임.

• 질병이 없는 사람을 수시로 양성으로 판정하는 검사법은 효용가치 X

---

2.1.3. 정밀도 (Precision)

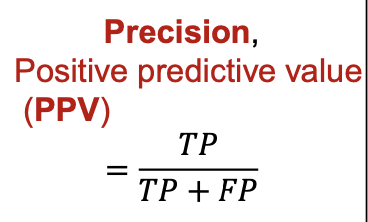
• Positive로 예측한 것 중, 진짜 Positive의 비율

• Positive에 집중한 평가지표임.

• FP(실제로는 틀렸는데, 맞다고 예측된 것)의 위험성이 높아 이를 최소화해야 하는 경우 사용

---

2.1.4. 재현율(Recall) = 민감도(Sensitivity)

• 의학/생물학 분야에서는 민감도라고 표현함.

• Positive로 예측한 것 중, 올바르게 Positive로 예측한 비율

• Positive에 집중한 평가지표임.

• FN(실제로는 맞는데 틀리다고 예측된 것)의 위험성이 높을 때 사용함
  ex. 음주 단속

---

2.1.5. F1-score

• 클래스 불균형 상황에서 효과적임.

• Precision과 Recall이 모두 중요한 경우를 위해 두 가지 모두를 고려하기 위한 Metric

• 이 둘의 조화평균을 구한 지표
  -> 이때 정밀도와 재현율이 어느 한쪽으로 치우치지 않는 수치를 나타낼 때 높은 값을 갖음.

출처
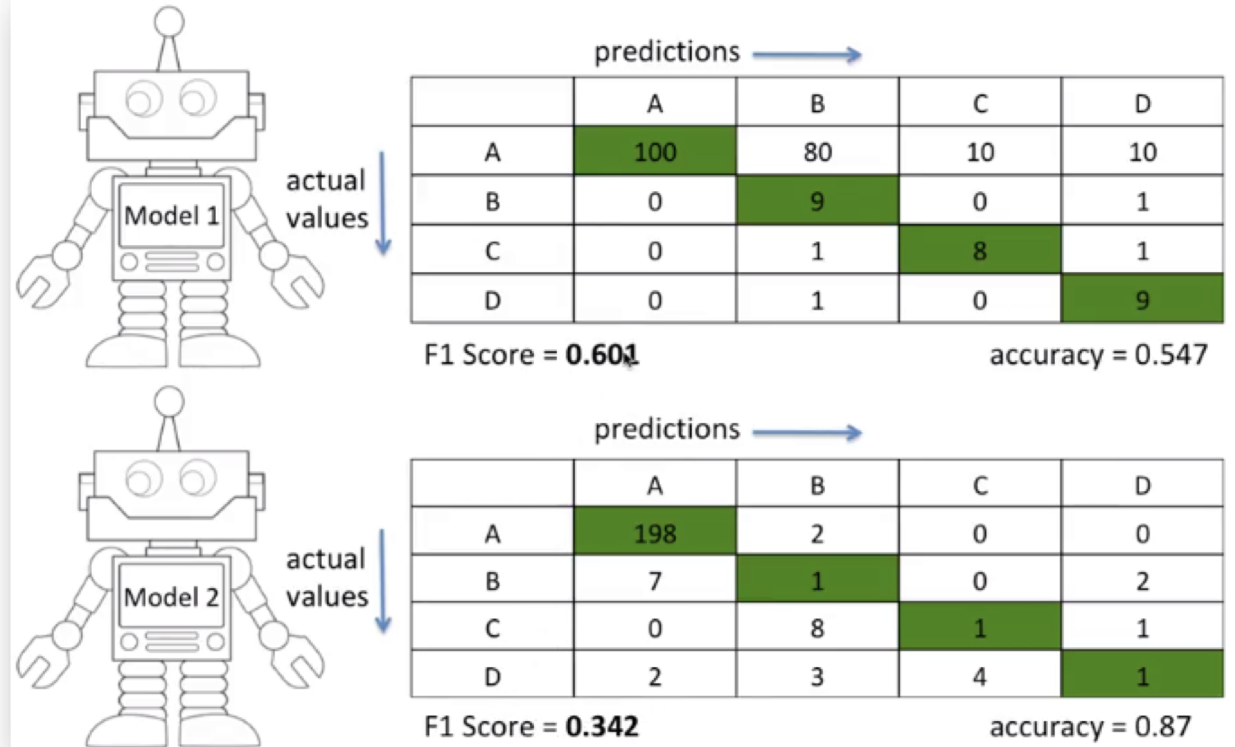
위의 그림에서 보면,

• Model1: B,C,D 클래스를 더 잘 맞춤

• Model2: A 클래스만 잘 맞춤 / 정확도는 0.87으로 Model1보다 더 높음

-> 하지만 F1 Score을 구해보면, Model1의 점수가 더 크게 산출됨.

Precision / Recall 서로 반비례 관계

• 임계값을 높일 경우, 정밀도 👍, 재현율 👎
  

• 임계값을 낮출 경우, 정밀도 👎, 재현율 👍
  

• threshold 값을 변화시켰을 때 재현율과 정밀도는 음의 상관관계를 갖음.

---

2.2. ROC-AUC

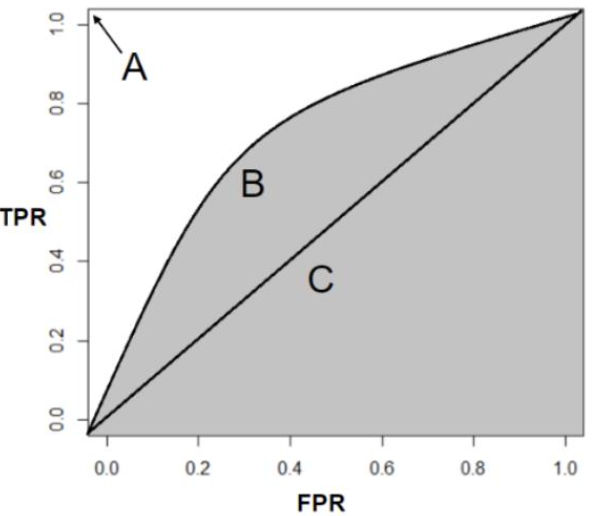
• ROC-AUC를 한마디로 표현하면 '맞으면 위로, 틀리면 오른쪽으로 그리는 커브의 아래 면적'을 의미함.

• Cut-off threshold에 대한 분류기의 성능을 보여주는 그래프

ROC

• Receiver Operating Characteristic

• 모든 임계값에서 분류 모델의 성능을 보여주는 그래프

AUC

• Area Under the Curve

• ROC 곡선 아래의 영역

• 위의 그림에서 회색으로 음영칠한 부분이 AUC임.

출처

1번

• True Positive rate
  암 환자를 올바르게 분류하는 비율 (실제 양성 중 양성으로 맞게 예측한 비율)
  -> 재현율(Recall)
  

• False positive rate
  = 1-특이도(specificity)
  암 환자가 아닌 사람을 암 환자로 분류하는 비율
  (실제 음성 중 양성으로 잘못 예측한 비율)

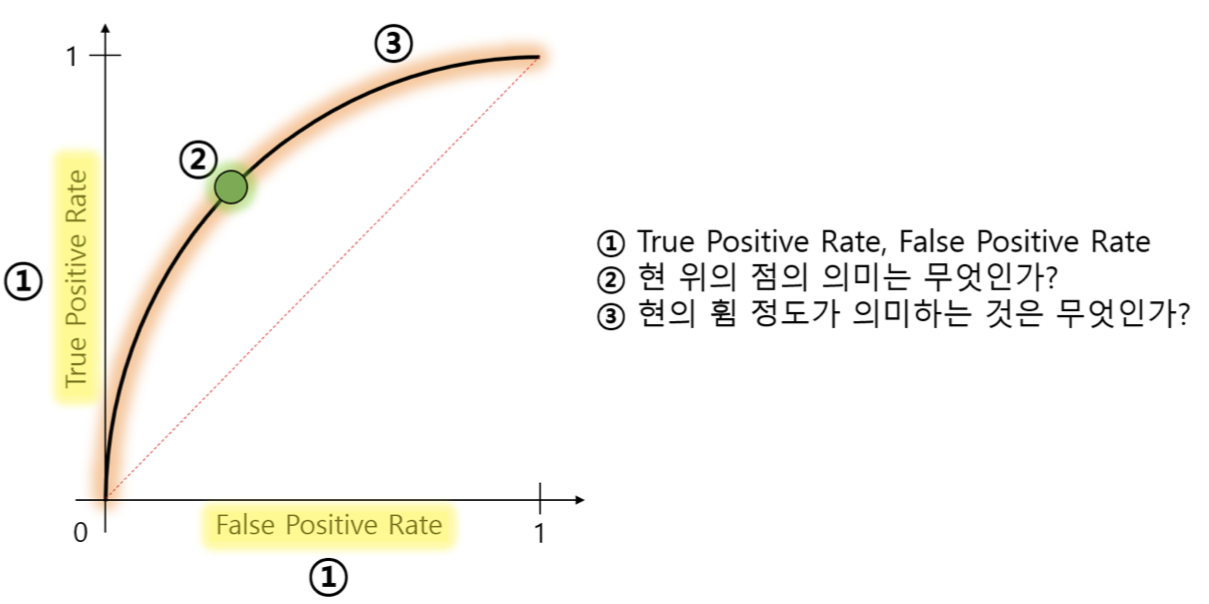
2번

• 현 위의 점의 의미
  : 모든 Threshold에서 False positive rate와 True positive rate의 비율을 Plotting한 것
  -> 분류기의 성능은 변하지 않음.

3번

• 현의 휨 정도의 의미
  : 두 클래스를 더 잘 구별할 수 있다면 ROC 커브는 좌상단에 가까워지게 됨.

🤜 Input

fig, ax = plt.subplots(1, 1, figsize = (8,6))
plot_roc_curve(dummy, X_test, y_test, ax=ax)
plt_roc_curve(tree, X_testm y_test, ax=ax)
plt_roc_curve(logit, X_testm y_test, ax=ax)
ax.set_title('ROC curve')
plt.show()

🖥️ Output

---

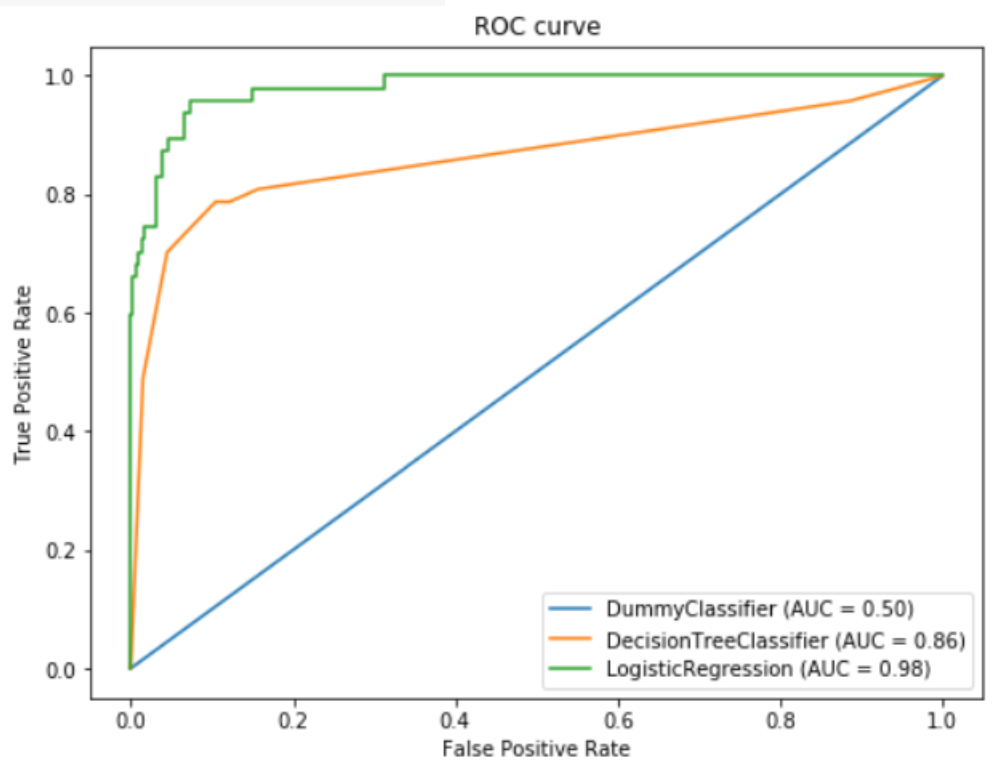
🎯 Summary

• 분류평가지표는 봐도봐도 헷갈리지만, 한번 정리하고나니 외워진거같기도...? 정말 중요한 개념이다.

• ROC-AUC의 의미와 Recall과 Precision이 왜 trade-off 관계인지를 이해하는 것이 이번 챕터의 핵심이다.

📚 References

• 권철민(2019),'파이썬 머신러닝 완벽 가이드[개정2판]', 위키북스, pp.116-126.

• 분류평가지표_오차행렬 이미지 출처 : https://en.wikipedia.org/wiki/Confusion_matrix

• 분류평가지표_ROC/AUC : https://ysyblog.tistory.com/72

• ROC-AUC 그림: https://angeloyeo.github.io/2020/08/05/ROC.html

• F1 score 그림: https://www.youtube.com/watch?v=8DbC39cvvis