가설검정
가설검정과 유의수준
가설 : 주어진 사실, 또는 조사하려고 하는 사실에 대한 주장 또는 추축
통계학에서는 특히, 모수를 추정할 때 모수가 어떠하다는 증명하고 싶은 추축이나 주장
귀무가설 : H0, 기존의 사실, 연구목적 아니며, 연구하고자 하는 가설의 반대가설
대립가설 : H1, 데이터로부터 나온 주장하고 싶은 가설, 또는 연구의 목적으로 귀무가설의 반대
제1종 오류 : 귀무가설이 참이지만, 귀무가설을 기각하는 오류
H0을 기각할 확률이 a라고하면 채택하게될 확률은 1-a
제1종오류를 범할 확률의 최대허용 한계를 유의수준이라고 하며 a라고 표시
제2종오류 : 귀무가설이 기각해야하지만, 귀무가설을 채택하는 오류
검정통계량 : 귀무가설이 참이라는 가정하에 얻은 통계량
검정결과 대립가설을 선택하게 되면 귀무가설을 기각함
검정결과 귀무가설을 선택하게되면 귀무가설을 기각하지 못한다 고 표현함
P-value : 귀무가설이 참일 확률
0~1 사이의 표준화된 지표
귀무가설이 참이라는 가정하에 통계량이 귀무가설을 얼마나 지지하는지를 나타낼 확률
기각역 : 귀무가설을 기각시키는 검정통계량의 관측값의 영역
가설 검정의 절차
가설 수립 -> 유의수준 결정 -> 기각역 설정 -> 검정통계량 계산 -> 의사결정
양측검정 : 대립가설의 내용이 같지않다 또는 차이가 있다 등 양쪽방향의 주장
ex) A백신과 B백신의 코로나 면역력에는 차이가 있다.
A팀과 B팀의 평균연봉은 차이가 있다.
단측검정 : 한쪽만 검증하는 방식으로 대립가설의 내용이 크다, 작다 처럼 한쪽방향의 주장
ex) A제품의 수율이 B제품의 수율보다 크다
A팀의 평균연봉이 B팀의 평균연봉보다 크다
단일 표본에 대한 가설 검정
모평균 가설검정 - 모분산 아는 경우
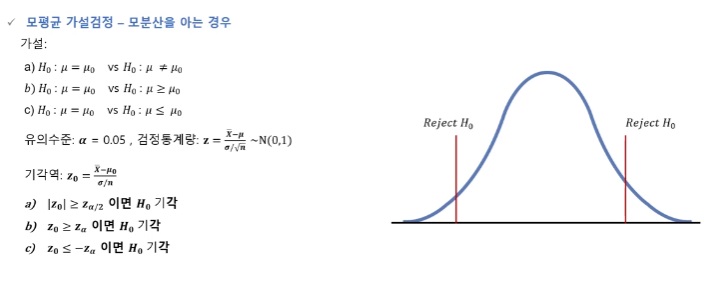
모평균 가설검정 - 모분산 모르는 경우

두개의 표본에 대한 가설검정
대표본 - 모분산을 아는 경우
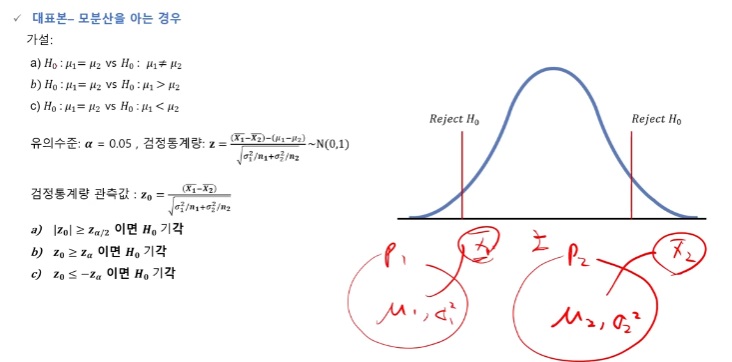
소표본 - 모분산을 모르는 경우

범주형 자료분석
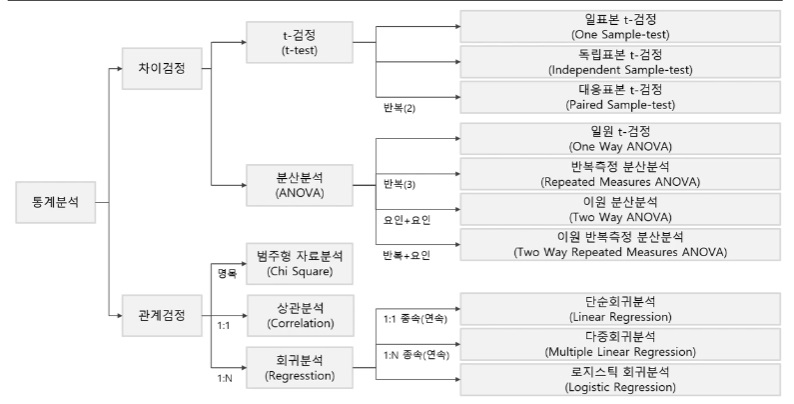
범주형 자료분석은 데이터 간 관계를 보는 분석
범주형 자료 : 관측된 결과를 어떤 속성에 따라 몇 개의 범주로 분류시켜 도수로 주어진 데이터
범주형 자료분석 : 범주형 자료에 대한 통계적 추론 방법
범주형 자료분석은 카이제곱 검정으로 추론함
ex) 대선에서 각 정당의 연령대별 지지율이 지난 대선의 지지율과 동일한가?
성별에 따라서 선호하는 핸드폰 회사가 동일한가?
적합도 검정
적합도 검정 : 관측된 값들이 추론하는 분포를 따르고 있는지 검정, 한개의 요인 대상으로 검정
독립성 검정 : 관측된 값을 두개의 요인으로 분할, 각 요인이 다른 요인에 영향 끼치는지 검정
동질성 검정 : 서로 다른 세개 이상의 모집단으로 관측된 값들이 범주내 동일 비율 나타내는지 검정