모집단과 표본분포
모집단은 전체(Population), 표본은 그중 일부(sample)
ex) 유권자 중 일부를 출구조사해서 당선자 예상
모평균, 모분산과 표본평균, 표본분산
표본추출(sampling) 모집단에서 표본을 추출, 모집단의 특성을 추론
표본추출에는 여러 방법이 있음
복원추출 : 모집단에서 데이터 추출할 때 하나 추출하고 다시넣고 추출하는 방법으로,
동일한 표본 추출될 수 있음
비복원추출 : 하나 추출하고 다시넣지않고 추출
Random Sampling : 편향되지 않도록 각 개체가 모두 동일한 확률로 추출하는 방법
불균형 데이터의 문제
데이터가 불균형데이터일 경우 문제 발생
우리가 예측모형을 만드는 목적은 관심있는 대상에 대한 확률을 예측하는데,
예측 대상이 전체대비 아주 낮다면 모형의 성능이 괜찮은가?
그래서 Sampling 기법을 통해 해결 or 모델을 통한 성능개선으로 불균형 문제를 해결
Sampling 기법
관심의 대상이 아주 비율이 낮은 경우
over sampling : 타겟 데이터 적은 class의 수를 많은 class의 비율만큼 증가
(일정비율로 복원추출)
but 과도적합의 문제 발생할 수 있음
under sampling : 타겟 데이터의 많은 class 수를 적은 class의 비율만큼 감소
임의로 뽑은 데이터가 편향될 수 있고, 모형의 성능이 떨어질 수 있음
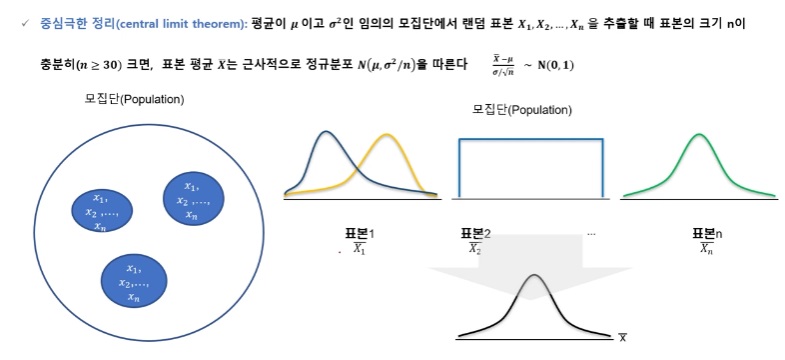
표본분포
통계량 : 표본에 기초하여 계산되는 수치함수를 통계량이라고 함
표본분포 : 통계량들이 이루는 분포를 표본분포라고 함
표본평균

중심극한 정리(매우중요)
카이제곱 분포
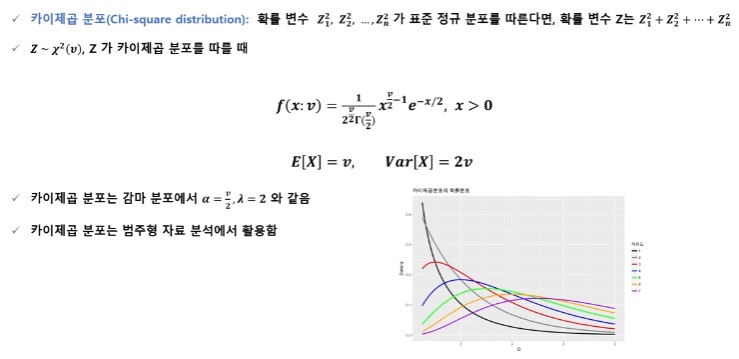
자유도 : 표본수 - 제약조건의 수 또는 표본수-추정해야하는 모수의 수(일반적으로 n-1)
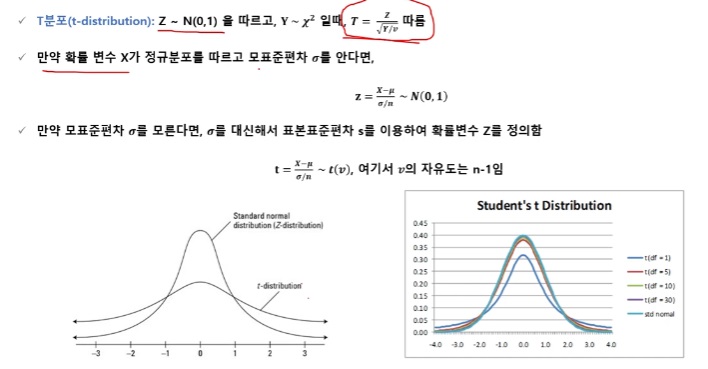
T분포
F분포

추정
추정(estimation) : 모집단의 모수를 모를경우,
표본으로 추출된 통계량을 모집단의 근사값으로 사용하는것
추정량 : 표본평균으로 모평균을 추정할 때, 표본평균을 모평균에 대한 추정량이라고 함
모수를 추정하는 방법에는 점추정, 구간 추정 있음
점추정 : 모수를 하나의 특정값으로 추정
일치성 : 표본의 크기가 모집단 크기에 근접해야함
표본이 크기가 크면 클수록(모집단에 가까울수록) 추정량 오차가 작아짐
불편성: 추정량이 모수와 같아야함
유효성: 추정량의 분산이 최소값이어야함
평균오차제곱 : 평균오차제곱이 최소값이어야함구간추정 : 모수가 포함될 수 있는 구간을 추정
신뢰구간 : 추정값이 존재하는 구간에 모수가 포함될 확률
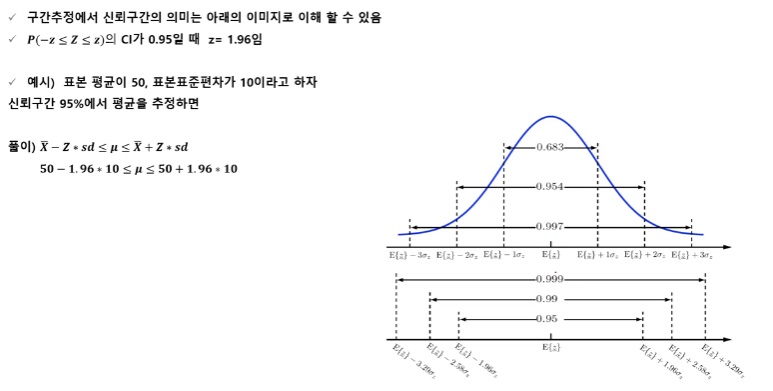
모평균의 구간 추정
-
모집단의 분산을 아는 경우 (실제로는 거의 불가능)

-
모집단의 분산을 모르는 경우

표본의 크기 결정
허용오차 : 추정한 값이 틀려도 허용할 수 있는 오차
정규분포의 신뢰구간을 통해 허용오차를 계산
모비율의 추정
모비율의 점추정
비율에 대한 추정으로 우리가 원하는 속성(class)에 속하면 '1' 아니면 '0'일때,
1의 속성을 갖는것의 개수를 X라고 하면 X ~ B(n,p)임
이 때 모비율의 점추정량을 표본 비율 이라고 함
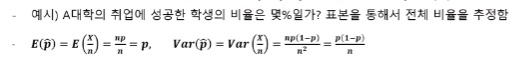
모비율의 구간추정
모비율 구간 추정에서 정규분포의 근사가 가능한 대표본은 보통 np>5, N(1-P)>5를 동시에 만족
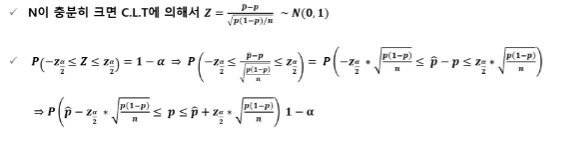

모평균 차이의 추정(점추정과 구간추정)

모평균 차이의 추정(구간추정 : 소표본, 모분산을 모르는 경우)

- 합동분산 추정량 식 외우기
모비율 차이의 추정(점추정과 구간추정)

