다층 퍼셉트론
퍼셉트론 : 선형 분류기(linear classifier) 한계
: 선형 분리 불가능한 상황에서 일정한 양의 오류
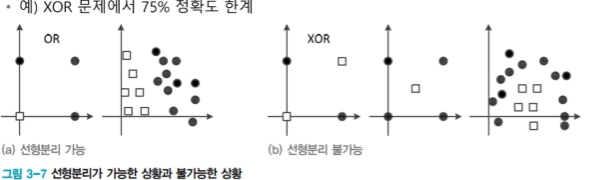
다층 퍼셉트론의 핵십 아이디어
- 은익층을 둔다. 은닉층은 원래 특징 공간을 분류하는 데 훨씬 유리한 새로운 특징 공간으로 변환한다.
- 시그모이드 활성함수를 도입한다. 퍼셉트론은 계단함수를 활성함수로 사용하였다. 이 함수는 경성hard 의사결정에 해당한다. 반면, 다층 퍼셉트론은 연성(soft) 의사결정이 가능한 시그모이드함수를 활성함수로 사용한다. 연성에서는 출력이 연속값인데, 출력을 신뢰도로 간주함으로써 더 융통성 있게 의사결정을 할 수 있다.
- 오류 역전파 알고리즘을 사용한다. 다층 퍼셉트론은 여러 층이 순차적으로 이어진 구조이므로, 역방향으로 진행하면서 한 번에 한 층씩 그레이디언트를 계산하고 가중치를 갱신하는 방식의 오류 역전파 알고리즘을 사용한다.
특징 공간 변환
퍼셉트론 2개를 사용한 XOR 문제의 해결
퍼셉트론 1 과 퍼셉트론 2가 모두 +1이면 ●부류 이고 그렇지 않으면 □부류임
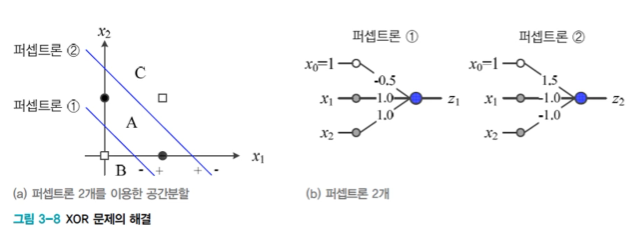
퍼셉트론 2개를 병렬 결합하면,
: 원래공간 x = (x1,x2)^T 를 새로운 공간 z = (z1, z2)^T로 변환
-> 새로운 특징공간 z에서 선형분리 가능함
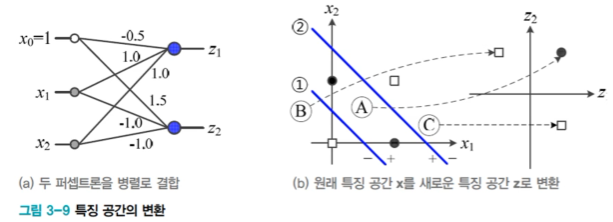
: 사람이 수작업 특징 학습을 수행한 것과 유사함 = 표현학습
추가 퍼셉트론 1개를 순차 결합하면,
: 새로운 특징공간z을 선형 분리를 수행하는 퍼셉트론 3을 순차결합하면 다층퍼셉트론이 됨.
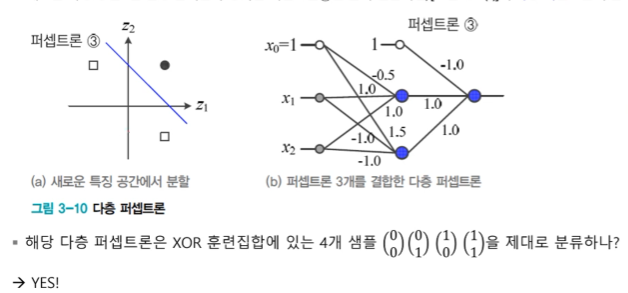
새로운 공간을 만들 고 선형 분리하는 퍼셉트론을 순차결합하면 다층 퍼셉트론이 된다.
다층 퍼셉트론의 용랑(capacity)
: 2차원 공간을 7개 영역으로 나누고 각 영역을 3차원 점으로 변환
: 계단 함수를 활성함수 T 로 사용을 가정했으므로 영역을 점으로 변환
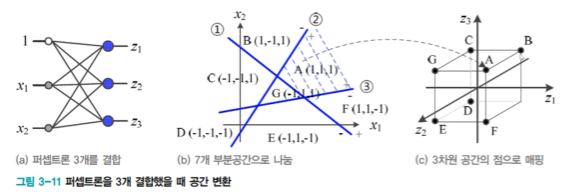
: p개 퍼셉트론을 결합하면 p차원 공간으로 변환
활성함수
딱딱한 공간 분할과 부드러운 공간 분할
: 계단 함수는 딱딱한 의사결정 - > 영역을 점으로 변환
: 그외 활성함수는 부드러운 의사결정 -> 영역을 영역으로 변환
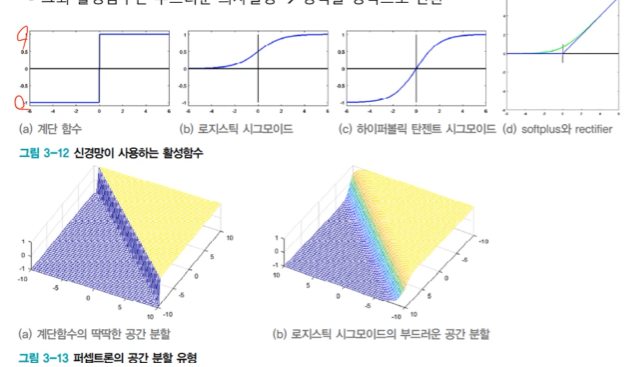
대표적인 비선형 함수인 S자 모양의(sigmoid)를 활성함수로 사용
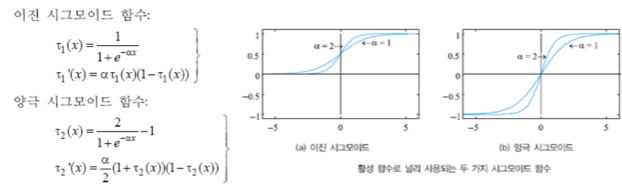
이진 시그모이드 함수 -> 0 ~ 1
양극 시그모이드 함수 -> -1 ~ 1
알파 값으로 시그모이드 함수의 형태를 조절 가능하다.
: 활성 함수에 따른 다층 퍼셉트론의 공간 분할 능력 변화(경성 부분 변화)

신경망이 사용하는 다양한 활성함수
: logistic sigmoid 와 tanh는 a가 커질수록 계단함수에 가까워짐
: 모두 1차 도함수 계산이 빠름 (특히, ReLU 는 비교 연산 한 번)

깊은 신경망에서는 ReLU를 많이 사용, 은닉층에서는 logistic sigmoid 사용
구조
입력 - 은닉층 - 출력의 2층 구조
: d+1 개의 입력 노드(d는 특징의 개수). c개의 출력노드(c는 부루 개수)
: p개의 은닉 노드: p는 하이퍼 매개변수(사용자가 정해주는 매개변수)
-> p가 너무 크면 과잉적합, 너무 작으면 과조 적합 => 하이퍼 매개변수 최적화
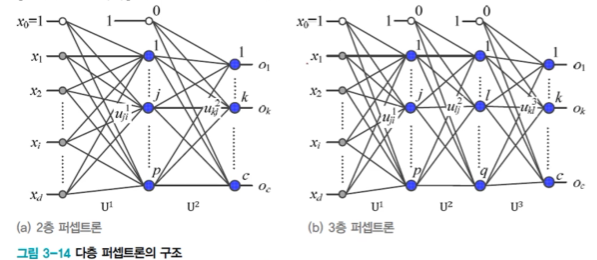
2층 다층퍼셉트론의 매개변수(가중치)
입력 - 은닉층 을 연결하는 U1
은닉층 - 출력을 연결하는 U2

입력을 0 번째 은닉층, 출력을 마지막 은닉층으로 간주
동작
특징 벡터 x를 출력 o로 사상(mapping)하는 함수로 간주할 수 있음
2층 퍼셉트론 : o = f(x) = f2(f1(x))
3층 퍼셉트론 : o = f(x) = f3(f2(f1(x)))
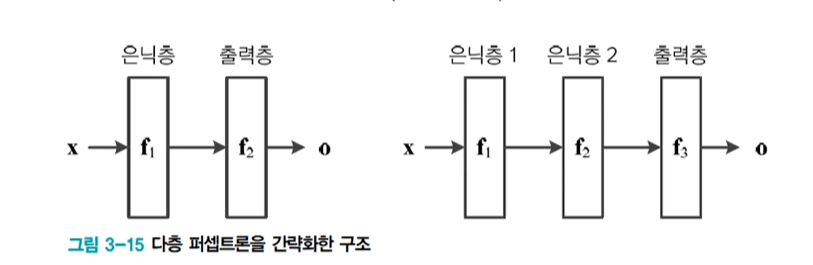
깊은 신경망은 o = fL(...f2(f1(x))), L >=4 4개 이상을 의미
노드가 수행하는 연산을 구체적으로 쓰면,

다층 퍼셉트론의 동작을 행렬로 표기하면
o = T(U^2 Th(U^1x))
은닉층은 특징 추출기
: 은닉층은 특징 벡터를 부류에 더 유리한 새로운 특징 고간으로 변환
: 현대 기계학습에서는 특징학습(feature learning, data driven features)이라 부름
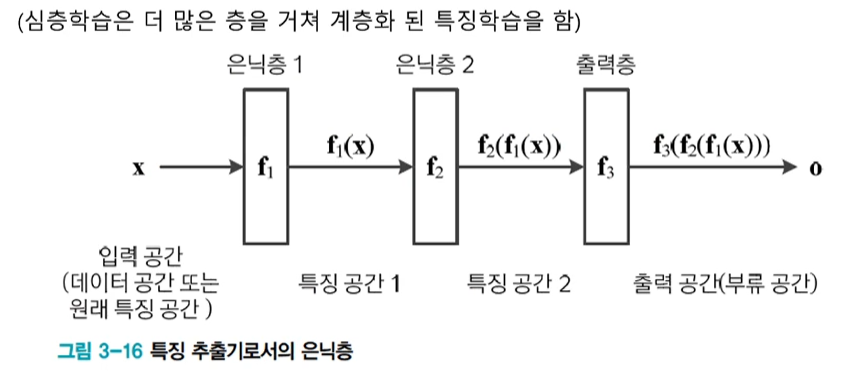
기본 구조
: 범용적 근사 이론(universal approximation theorem)
-> 하나의 은닉층은 함수의 근사를 표현
-> 다층 퍼셉트론도 공간을 변환하는 근사함수
: 얕은 은닉층의 구조
-> 지수적으로 더 넓은 폭이 필요할 수 있음
-> 더 과잉적합 되기 쉬움
-> 일반적으로 깊은 은닉층의 구조가 좋은 성능을 가짐
은닉층의 깊이에 따른 이점
: 지수의 표현(exponential representation)
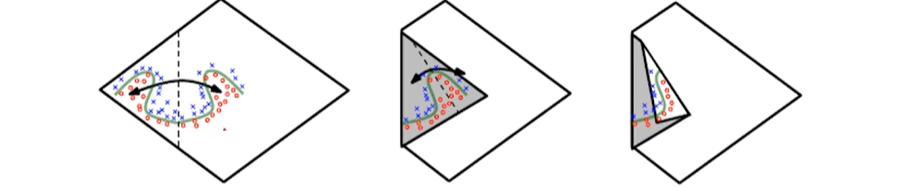
-> 각 은닉층은 입력 공간을 어디서 접을지 지정 => 지수적으로 많은 선형적인 영역 조각들
: 성능 향상
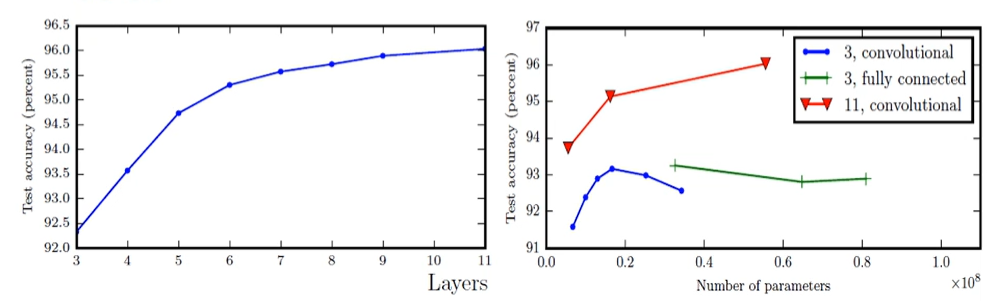
다층 퍼셉트론에 의한 인식
다층 퍼셉트론 학습 과정
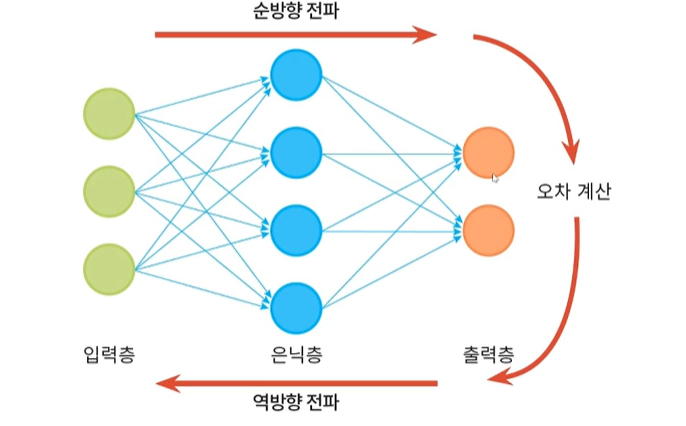
순방향 전파 : 입력층 -> 은닉층 -> 출력층
역방향 전파 : 오차계산 -> 층방향 수정
예측단계
: 학습을 마친 후 현장 설치하여 사용( 또는 테스트 집합으로 성능 테스트)
: y = argmaxO
: 전방 계산 한번만 사용하므로 빠름
오류 역전파 알고리즘의 빠른 속도
연산 복잡도 비교
: 오류 역전파 전방 계산 대비 약 1.5~2배의 시간 소요 = 비교적 빠름(연쇄법칙)
-> c:분류 수 , d : 특징차원, p:은닉층 차원
:학습 알고리즘은 오류 역전파 반복하여 점근적 시간 복잡도는 세타((cp+dp)nq)
-> n : 훈련집합의 크기, q : 세대(epoch) 수
- 은닉층을 하나만 가진 다층 퍼셉트론은 범용근사자
: 은닉 노드가 충분히 많다면, 포화(활성)함수로 무엇을 사용하든 표준 다층 퍼셉트론은 어떤 함수라도 원하는 정확도 만큼 근사화할 수 있다.
성능향상을 위한 경험의 중요성
순수한 최적화 알고리즘으로는 높은 성능 불가능
: 데이터 희소성, 잡음, 미숙한 신경망 구조 등 이유
: 성능 향상을 위한 다양한 경험을 개발하고 공유함
신경망의 경험적 개발에서 중요 쟁점
-
아키텍처 : 은닉층과 은닉 노드의 개수를 정해야 한다. 은닉층과 은닉 노드를 늘리면 신경망의 용량은 커지는 대신, 추정할 매개변수가 많아지고 학습 과정에서 과잉적합할 가능성이 커진다. 현대 기계학습은 복잡한 모델을 사용하되, 적절한 규제 기법을 적용하는 경향이 있다.
-
초기값 : 보통 난수를 생성하여 설정하는데, 값의 범위와 분포가 중요하다.
-
학습률 : 처음부터 끝가지 같은 학습률을 사용하는 방식과 처음에는 큰 값으로 시작하고 점점 줄이는 적응적 방식이 있다.
-
활성함수 : 초창기 다층 퍼셉트론은 주로 로지스틱 시그모이드나 tanh 함수를 사용했는데, 은닉층의 개수를 늘림에 따라 그레이디언트 소멸과 같은 몇 가지 문제가 발생한다. 따라서 깊은 신경망은 주로 ReLU함수를 사용한다.
오류 역전파 알고리즘
특징공간 - > 특닉층을 통한 특징공간의 변환
행렬 곱 : 회전
편향 : 이동
비선형 함수 : 왜곡
목적함수의 정의
훈련집합
: 특징 베거 집합과 부류 벡터 집합
: 부류 벡터는 단발성 코드로 표현됨.
: 설계 행렬로 쓰면,
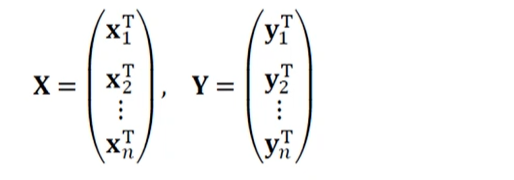
기계학습의 목표
: X,Y에서 모든 샘플을 옳게 부류하는 함수 f를 찾는 일
Y = f(x)
목적함수
: 평균 제곱 오차(mean squared error(MSE))로 정의
-> 온라인 모드 : 계속 들어오는 값을 구함
-> 배치 모드 : n개 만큼 평균값을 구하고 결과를 확인
오류 역전파 알고리즘의 설계
간단한 전방전파와 오류역전파의 연산 그래프 예
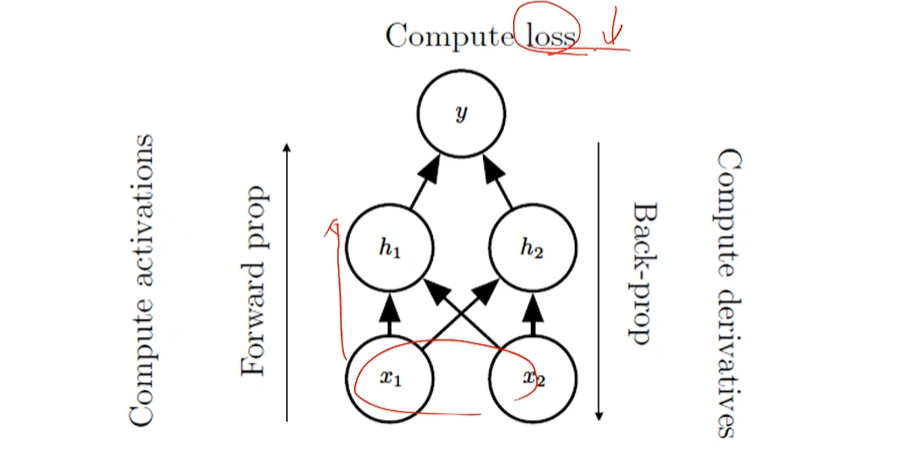
- Compute Loss
- Compute activations, Forward prop
- Compute derrivatives, Back prop
연산 그래프의 예
: 전방 연산을 그래프로 표현
- z = xy
- logistic regression
-> y^ = s(xTw + b) - ReLU activation
-> H = max{0, XW + b} - linear regression
-> w : weights
-> y : prediction
-> lamda(sigma)w^2 : weight decay penalty
연쇄 법칙의 구현
: 반복되는 부분식들(subexperessions)을 저장하거나 재연산을 최소화
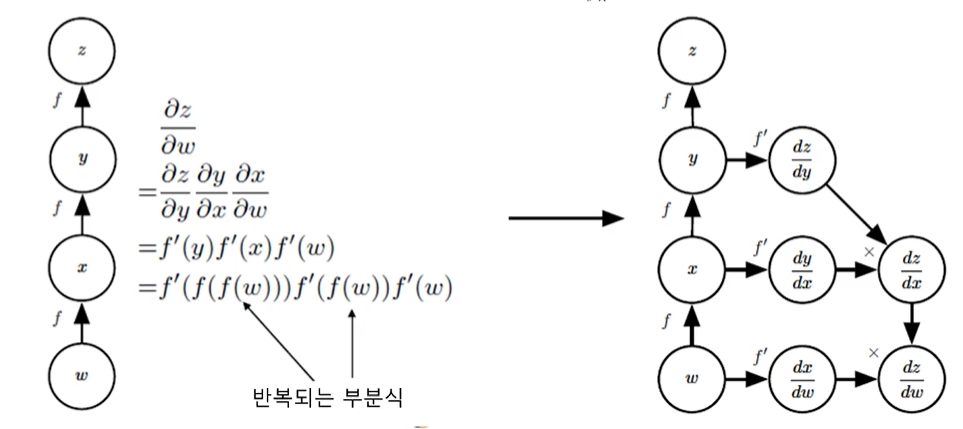
연쇄 법칙(chain rule)
= 미분들의 조합
끝에서 부터 나오는 오류 신호에 가중치가 전달되고 있다.
가중치를 변화 시켰을 때 에러가 변하는 것을 부분부분 나누는 것.
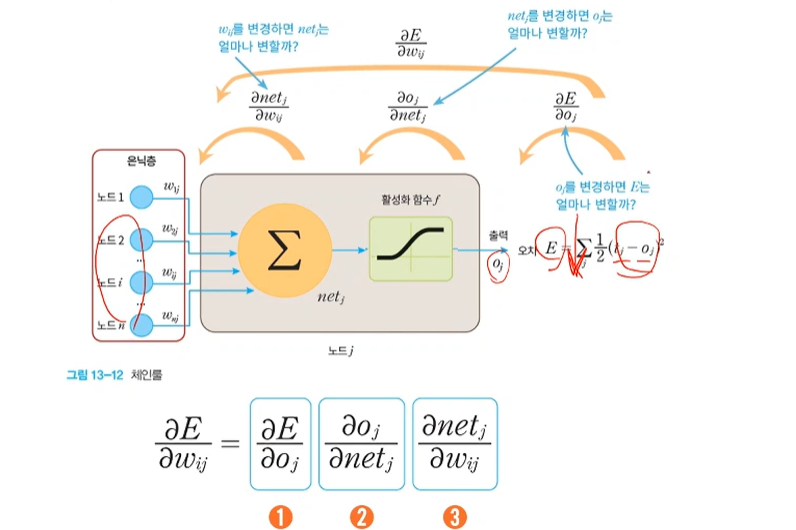
목적함수는 = J(세타) = J({U1, U2})의 최젖점을 찾아주는 경사 하강법
알고리즘의 형태

오류 역전파의 유도
mes -> 관심있는 k번째 요소만 나머지 상수 제거 -> 연쇄법칙 - > ok = T(osumk == uk^2z) 대입 -> 활성함수 미분 -> osum 미분
오류 역전파 알고리즘
출력의 오류를 역방향으로 전파아며 경사도를 계산하는 알고리즘
반복되는 부분식들의 경사도의 지수적 폭발(exponenrial ecplosion)혹은 사라짐(vanishing)을 피해야 함
역전파 분해 (backprop with scalars)
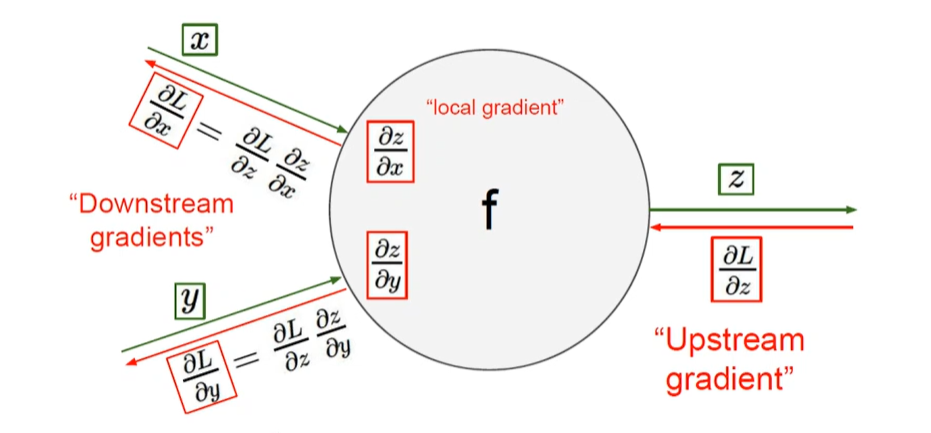
단일 노드 역전파의 예
forward : in -> f(x) -> out ( 실제와의 차이 , error)
backprop : out -> (error) -> f(x) -> in
곱셉의 역전파의 예
forward : in1 + in2 => x => out
backprop : 해당하는 위치에 있는 것을 나누는 것
outputgradient *localgrdient(in1 or in2)

덧셈의 역전파 예
out = sigma ini
forward : ini -> sigma(all +) -> out
backprop : output에 따른 outputgradient, localgradient (해당 값에 대해 미분 하면 그 값만 남으므로 1이 된다) ==> 곱하면 outputgradient
sum(froward) <=>fanout(backprop)
s자 모양 활성함수의 역전파 예
out = (sigmoid)in
forward : in -> 함수 -> out
backprop : out -> 함수 -> in
outputgradient x sigmoid의 미분[sigmoid(in)1-sigmoid(in)]
최대화의 역전파 예
out = max{ini}
forward : ini -> max -> out
backprop : out -> max -> ini
전개(fanout)의 역전파 예
multivariable chain rule
forward : t -> x , y -> z
let
-> x = x(t), y = y(t) , z = f(x, y)
backprop : z - > x, y -> t
fanout(frward) <=> sum(backprop)
주요 예
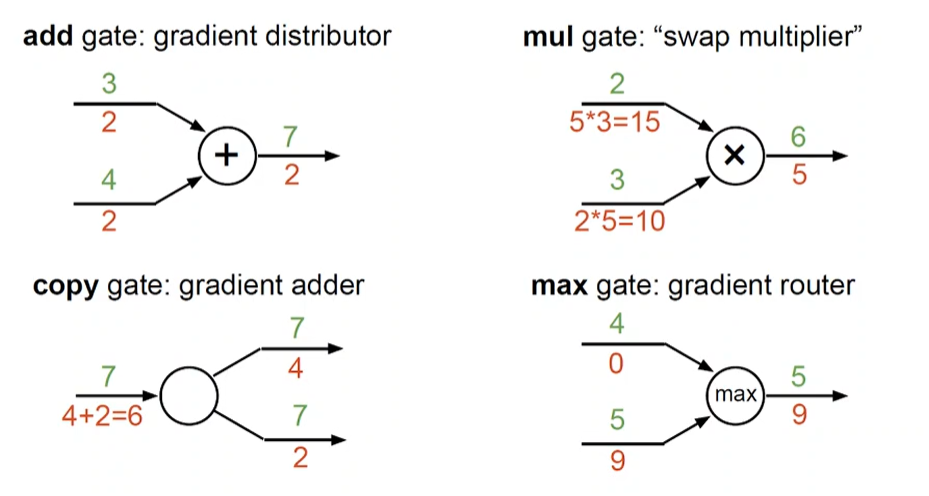
실제 역전파 예
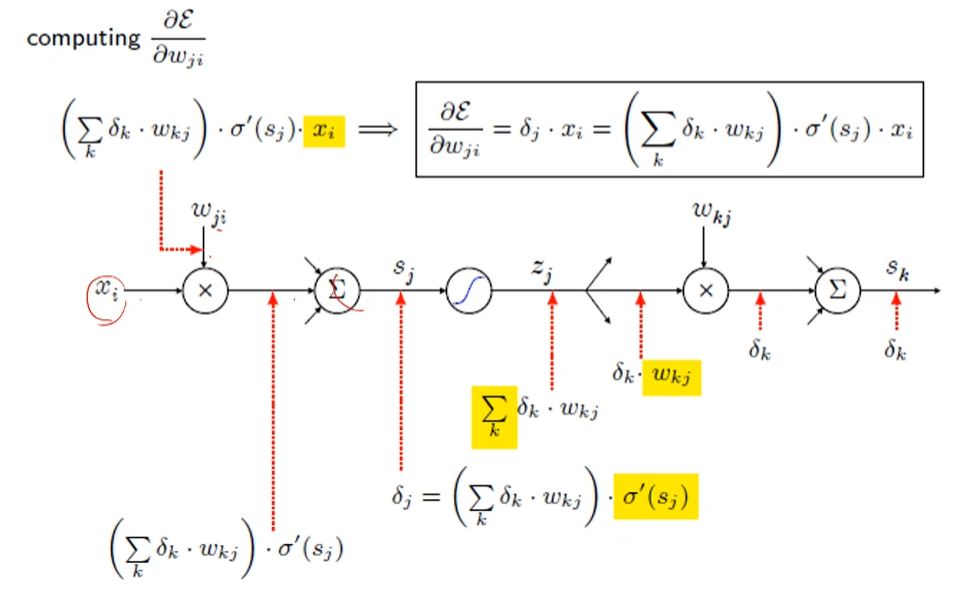
확률론적 경사 하강법

도함수(derivatives, 미분)의 종류
Scalar to Scalar : Regular derivative
Vector to Scalar : Drivative is Gradeient
Vector to Vector : Derivative is Jacobian
chain rule에 의해서 Scalar(결과값)를 Vector(가중치)로 미분하는 것은 야코비안 행렬(은닉층 벡터를 가중치 벡터로 미분)과 gradient(결과값을 은닉층 베거로 미분)의 곱으로 나타나게 된다.
미니 배치 확률론적 경사 하강법
미니배치 방식
: 한번에 t개의 샘플을 처리(t는 미니배치 크기)
t=1이면 확률론적 경사 하강법
t=n(전체)이면 배치 경사 하강법
: 미니 배치 방식은 보통 t = 수십~수백
경사도의 잡음을 줄여주는 효과 때문에 수렴이 빨라짐
GPU를 사용한 병렬처리에도 유리함
-> 현대 기계학습은 미니배치 기반의 확률론적 경사하강법을 표준처럼 여겨 널리 사용함
