Collaborative Filtering (2)

00. 학습 내용

• Model Based Collaborative Filtering에 대하여 학습
• Singular Value Decomposition에 대하여 학습
• Matrix Factorization에 대하여 학습
• Bayesian Personalized Ranking에 대하여 학습

01. Model Based Collaborative Filtering

1) Collaborative Filtering 분류

• Neighborhood-based Collaborative Filtering
  • User-based
  • Item-based
• Model-based Collaborative Filtering
  • Singular Value Decomposition
  • Matrix Factorization (SGD, ALS, BPR)
  • Deep Learning
• Hybrid Collaborative Filtering
  • Content-based Recommendation과의 결합

2) Model-based Collaborative Filtering

• Neighborhood-based Collaborative Filtering의 한계
  • Sparsity(희소성) 문제
    • 데이터가 충분하지 않다면 유사도 계산이 부정확해져 추천 성능이 감소
    • 데이터가 부족하거나 혹은 아예 없는 유저, 아이템의 경우 추천이 불가능(Cold start)
  • Scalability(확장성) 문제
    • 유저, 아이템이 많아야 정확한 예측을 하지만, 유저와 아이템이 늘어날수록 유사도 계산이 늘어나 시간이 오래 걸림

• Model-based Collaborative Filtering의 특징
  • 항목 간 유사성을 단순 비교하는 것에서 벗어나, 데이터에 내재된 유저-아이템 관계의 잠재적 특성/패턴을 찾아 추천하는 CF 기법
  • Parametric Machine Learning(이웃 기반 CF은 유저/아이템 벡터를 데이터를 통해 계산된 형태로 저장되는 Memory-based CF 지만, Model-based CF의 경우 유저와 아이템 벡터 모두 학습을 통해 변하는 파라미터)
  • 데이터 정보가 파라미터의 형태로 모델에 압축(주어진 데이터를 활용하여 모델의 파라미터인 Embedding, 가중치 등이 데이터의 패턴을 나타내는 방향으로, 그리고 최적화를 통해 업데이트 되고 이렇게 생성된 파라미터들이 추천을 위한 정보가 반영된 하나의 함수라고 할 수 있음)

• Model-based Collaborative Filtering의 장점
  • 모델 학습/서빙
    • 유저-아이템 데이터는 학습에만 사용되고, 학습된 모델은 압축된 형태로 저장되고, 압축된 형태로 저장된 모델을 통해 추천하기 때문에 서빙 속도가 빠름
  • Sparsity / Scalability 문제 개선
    • 이웃 기반 CF에 비해 sparse한 데이터에서도 좋은 성능을 보임 (NBCF와 달리 Sparsity Ratio가 99.5%가 넘을 경우에도 사용가능함)
  • Overfitting 방지
    • NBCF의 경우 특정 주변 이웃에 의해 크게 영향을 받지만, MBCF의 경우에는 전체 데이터의 패턴을 학습하도록 모델이 작동함
  • Limited Coverage 극복
    • 이웃 기반 CF의 경우 공통의 유저 / 아이템을 많이 공유해야만 유사도 값이 정확해지지만, 모델 기반 CF의 경우에는 모든 데이터의 내재된 패턴을 반영한 Embedding이 생성되어 유사도 계산이 더 정확함

3) Latent Factor Model

• Latent Factor Model은 유저와 아이템 관계를 잠재적 요인으로 표현할 수 있다고 보는 모델
  • 다양하고 복잡한 유저와 아이템의 특성을 몇 개의 벡터로 compact하게 표현
  • 유저 기반의 경우 유저와 아이템의 특성이 매우 sparse 한 형태의 벡터로 표현됨
• Latent Factor Model은 유저-아이템 행렬을 저차원의 행렬로 분해하는 방식으로 작동
  • 각 차원의 의미는 모델 학습을 통해 생성되며 표면적으로는 알 수 없다는 단점이 존재(그럼에도 각 차원에는 데이터의 패턴이 내재되어 있기 때문에 데이터만 많다면 좋은 성능을 보임)
• 학습된 Latent Factor Model의 벡터 공간에 유저와 아이템 벡터가 같은 공간에 놓일 경우 유저와 아이템의 유사한 정도를 확인할 수 있음
  • 유저 벡터와 아이템 벡터가 유사하게 놓인다면 해당 유저에게 해당 아이템이 추천될 확률이 높음
• 우리가 앞으로 다룰 Model-based Collaborative Filtering 대부분이 Latent Factor Model의 형태임

02. Singular Value Decomposition

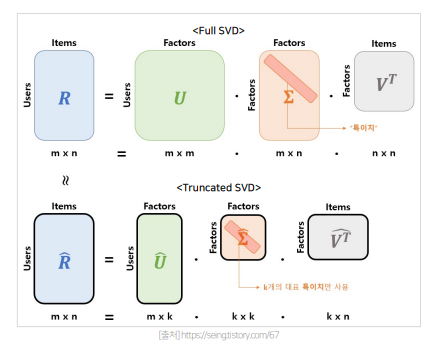
• SVD는 위 그림처럼 Rating Matrix에 대해 유저와 Latent Factor의 관계를 의미하는 U 행렬과 아이템과 Latent Factor의 관계라고 할 수 있는 V 행렬로 분해하여, 유저와 아이템에 K개의 잠재 요인을 얻는 방식이라고 할 수 있음
• 각각의 K개의 Latent Factor는 유추할 수 있을 뿐 정확히 무엇을 의미하는지 알 수 없음
• 얻은 K개의 Latent Factor 중 임의의 특이치만 뽑아서 사용함

• SVD 한계점
  • 분해하려는 행렬의 Knowledge가 불완전할 때 정의되지 않음
    • 대부분에 추천에 활용되는 살제 데이터는 결측치가 매우 많은 형태인 Sparse Matrix임
  • 따라서 결측된 entry를 모두 채우는 Imputation을 통해 Dense Matrix를 만들어 SVD를 수행함
    • 결측된 entry를 0 or 유저/아이템의 평균 평점으로 채우게 되면 데이터의 양을 상당히 증가시키므로, Computation 비용이 높아짐
    • 정확하지 않은 Imputation은 데이터를 왜곡시키고 예측 성능이 떨어짐
    • 행렬의 entry가 매우 적을 때 SVD를 적용하면 과적합이 발생하기 쉬움

SVD는 위와 같은 한계점이 존재하여, SVD의 원리를 이용하는 다른 접근 방식인 Matrix Factorization이 등장하게 됨

03. Matrix Factorization

1) 기본 개념

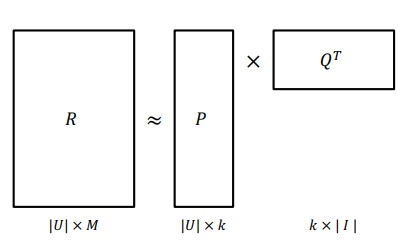
• SVD의 개념과 유사하게 User-Item 행렬을 저차원의 User와 Item의 latent factor 행렬의 곱으로 분해하는 방법이지만, 관측된 선호도(평점)만 모델링에 활용하고 관측되지 않은 선호도를 예측하는 일반적인 모델을 만드는 것이 목표
• Rating Matrix를 P와 Q로 분해하여 R과 최대한 유사한 $\hat{R}$을 추론하는 것이 목표

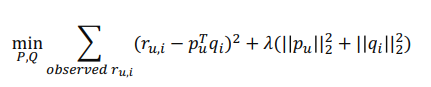
• 따라서 Objective Function은 위와 같이 구성됨
• r은 학습 데이터에 있는 유저 u의 아이템 i에 대한 실제 rating
• p와 q는 유저와 아이템의 latent vector
• 두번째 텀의 상수(람다)배된 penalty term은 L2-정규화(regularization)를 의미
  • weight를 loss function에 넣어줘 weight가 너무 커지지 않도록 제한 함으로써 overfitting을 방지

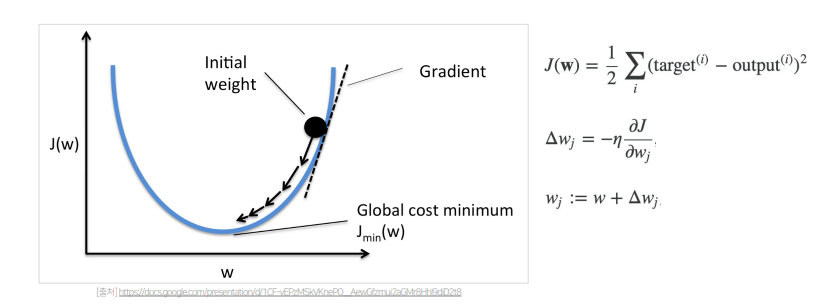
• 모델 학습은 Gradient의 반대방향으로 p와 q를 업데이트 하는 SGD를 이용함

2) 다양한 Matrix Factorization 테크닉

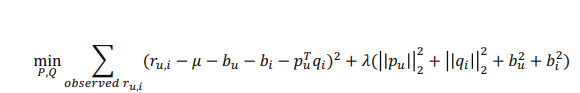
• R 예측에 전체 평균, 유저/아이템의 bias등을 추가하여 모델의 예측 성능을 높일 수 있음
• 어떤 유저는 모든 영화에 대해서 평점을 짜게 줄 수도, 어떤 아이템은 대체로 높은 평점을 받을 수도, 이러한 다양한 특징들은 bias로 두어 학습함으로써 모델의 표현력을 높일 수 있음

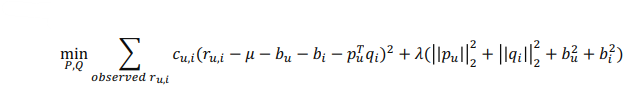
• 모든 평점이 동일한 신뢰도를 갖지 않기 때문에, 신뢰도를 의미하는 Confidence Level를 추구하여 모델의 예측 성능을 높임
• 유저의 아이템에 대한 평점이 정확하지 않은 경우, 대규모 광고 집행과 같이 특정 아이템이 많이 노출되어 클릭되는 경우 등 각 평점은 신뢰도가 다를 수 있음

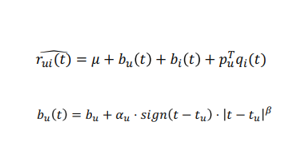
• 시간에 따라 변화는 유저, 아이템의 특성을 반영하고 싶을 때 학습 파라미터가 시간을 반영하도록 모델을 설계하여 모델의 예측 성능을 높일 수 있음
• 아이템이 시간이 지남에 따라 인기도가 떨어지고, 유저가 시간이 흐르면서 평점을 내리는 기준이 엄격해질 수 있음(실제로 MF 논문에서는 시간에 따른 영향력을 학습시켰을 때 모델의 성능이 더 높아졌다고 함)

3) Alternative Least Square

• 기존 SGD의 경우 p, q 두 파라미터가 한번 학습에 동시에 계속해서 업데이트됨
• 그런데 이렇게 p, q 파라미터가 계속 바뀌게 되면 목적함수 자체가 non-convex 해져, 모델이 불안정해짐
• 그래서 두 매트릭스 중 하나를 상수로 놓고 나머지 매트릭스를 업데이트하는 Alternative Least Square 방식이 생김
• 간단하게 정의하면 ALS는 p, q 가운데 하나를 고정하고 다른 하나로 least-square 문제를 푸는 것
• ALS는 두 메트릭스 중 하나를 상수로 고정하여 학습함으로써 목적함수가 quadratic form이 되어 convex해짐
• 이에 SGD 보다 Sparse한 데이터에 대해 SGD 보다 더 Robust 하고 대용량 데이터를 병렬 처리하여 빠른 학습 가능함(병렬 처리 기준임, 실제로 하나의 임베딩을 고정시키고 학습했을 때 모델이 성능이 더 높았던 경험이 있음)

04. Bayesian Personalized Ranking

• Bayesian Personalized Ranking은 베이지안 추론에 기반하여 Implicit data를 사용해 서로 다른 아이템에 대한 유저의 선호도를 반영하도록 모델링하는 방법임
• 본 논문 관련 포스팅