경사하강법(매운맛)

이번 장에서는 저번에 배운 경사하강법에서 조금 더 심화된 내용에 대하여 학습을 진행했다. 앞으로 배울 딥러닝의 역전파 알고리즘의 근간은 경사하강법이기 때문에 이번 장에서 경사하강법을 완벽히 이해할 수 있도록 노력했다.

00. 공부 내용

• 경사하강법으로 선형회귀 계수를 구하는 방법에 대하여 공부
• 확률적 경사하강법에 대하여 공부

01. 경사하강법을 이용한 선형회귀 계수 계산

• 우리는 앞서 정규 방정식을 활용해 회귀 계수를 구하는 방법을 학습했다.

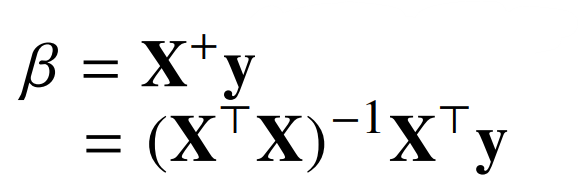
• 경사하강법을 이용해도 회귀 계수를 구할 수 있다.
• 다음과 같이 RMSE를 목적식으로 하여, 이를 최소화하는 베타를 구하면 된다.

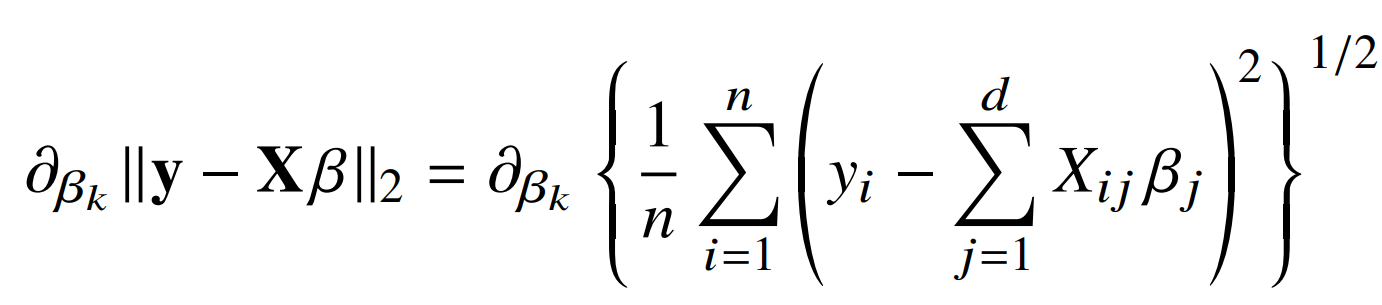
• 우리는 앞서 다변수 함수 일때는 각 변수에 따른 그레이더언트 벡터가 필요하다는 것을 배웠다. 따라서 다음과 같은 식을 통하여 각 베타에 따른 그레디언트 벡터를 구해야 한다. (본 식은 기존 식에 제곱을 하여 식을 조금 더 간단하게 표현한 것)

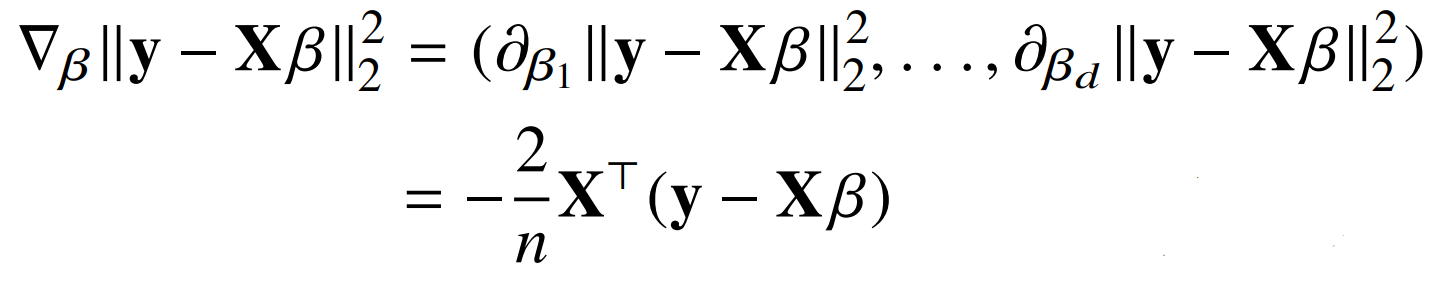
• 그리고 구한 그레디언트 벡터와 람다(학습률)를 이용하여 베타를 업데이터 시키면서 본 한수의 목적식을 최소화할 수 있는 최적의 회귀계수 베타를 구할 수 있다.

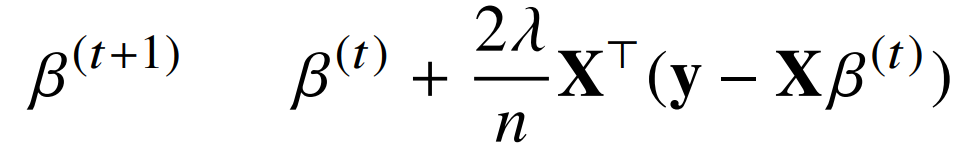
02. 확률적 경사하강법

• 이론적으로 경사하강법은 미분가능하고 convex(볼록)한 함수에 대해선 적절한 학습률과 학습횟수를 선택한다면 수렴이 보장된다.
• 하지만 비선형회귀 문제와 실존의 문제들은 무조건 convex한 함수식을 보장한다고 볼 수 없다. 따라서 전체 데이터를 모두 업데이트에 활용하는 경사하강법은 수렴이 항상 보장되지는 않는다.(local minima에 빠질 수 있음)
• 그러므로 우리는 데이터를 한개 또는 미니배치 단위로 활용해 목적식을 최적화하는 확률적 경사하강법을 이용하는 것이 좋다. (local minima에서 벗어날 가능성이 생김)
• 확률적 경사하강법을 이용한다면 배치 단위마다 서로 다른 목적식을 가지기 때문에 볼록이 아닌 함수에서도 확률적으로 최적화가 가능해질 수 있다.
• 또한 확률적 경사하강법은 매우 효율적인 연산이다. 예를 들어 100만x100만 이라는 데이터가 존재한다고 가정할 때, 이를 경사하강법 또는 정규방정식을 이용해 회귀계수를 찾는다고 할 때 100만 x 100만의 연산이 일어나 메모리가 부족해지는 Out-of-memory 현상이 발생할 수 있다. 하지만 확률적 경사하강법은 미니 배치단위만 적절하게 설정해준다면 Out-of-memory 현상이 발생하지 않는다.