경사하강법(순한맛)

이번 장에서는 미분과 경사하강법에 대하여 학습을 진행했다. 미분과 경사하강법은 딥러닝의 가장 기본 중의 기본이기 때문에 이번 학습을 통해서 기초를 완벽하게 다질 수 있어서 좋았다.

00. 공부 내용

• 미분에 대하여 공부
• 경사하강법에 대하여 공부

01. 미분

• 미분은 '변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구'로 제일 많이 사용되는 최적화 기법 중 하나이다.
• 미분은 변화율의 극한으로 정의된다.

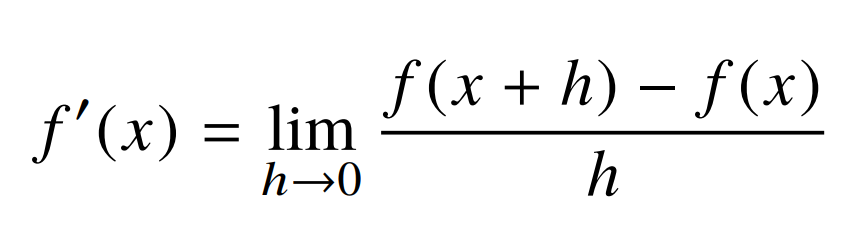
• 미분을 통해서 접선의 기울기를 알 수 있다.

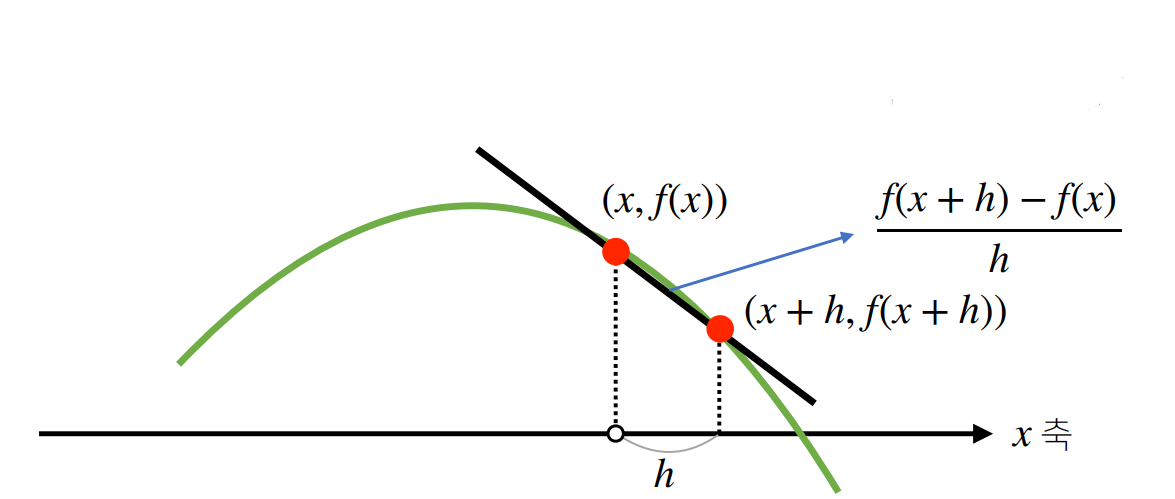
02. 경사하강법

• 앞서 미분을 통해서 접선의 기울기를 알 수 있다고 했다. 접선의 기울기를 알 수 있다면, 현재 함수를 증가 또는 감소 시킬 수 있는 방향을 알 수 있다. 다음과 같이 접선의 기울기가 음수일때 x 값을 감소시키면 함수는 최댓값을 찾아가고, 반대로 x 값을 증가시키면 함수는 최솟값을 찾아간다.

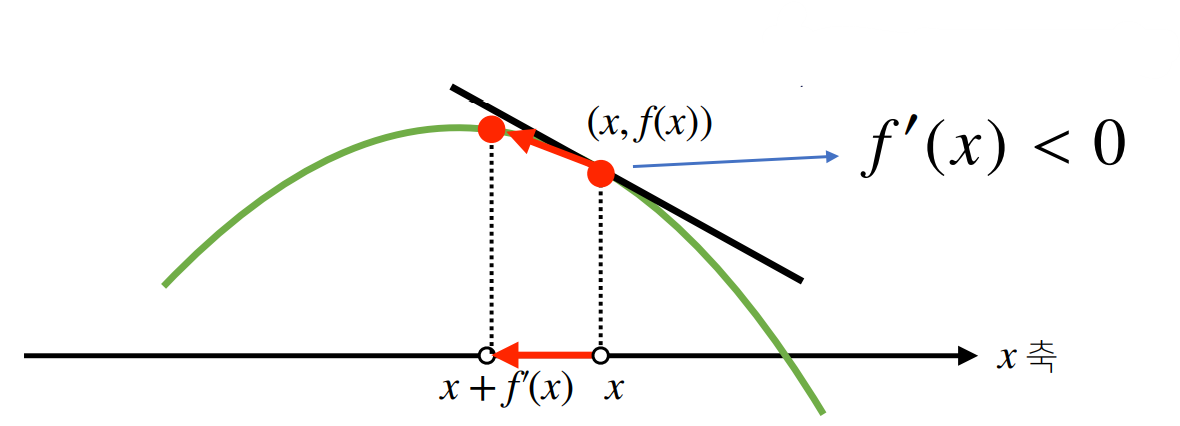
• 이러한 원리를 미분값을 기준으로 봤을때, 미분값을 더하면 함수는 극댓값을 찾아가고 이를 경사상승법이라고 하며, 미분값을 뺀다면 함수는 최솟값을 찾아고 이를 경사하강법이라고 한다.
• 또한 경사하강법이 편리한 이유 중에 하나는 함수가 극값 찾았을 때 기울기의 값은 0에 수렴하기 때문에 더 이상 업데이트가 이루어지지 않는다는 것이다.
• 이처럼 경사하강법을 이용하면 극값에 가까워질수록 기울기의 값은 작아져 점차 보폭이 작아지는 효과를 얻어 극값을 더 정교하게 찾을 수 있게 되는 것이다.
• 벡터가 입력인 다변수 함수의 경우 각 변수 마다의 그레디언트를 구해야하기 때문에 편미분을 사용하고, 각 변수 마다의 그레디언트의 모음을 그레이디언트 벡터라고 부르며, 본 그레디언트 벡터를 가지고 경사하강법 또는 경사상승법에 사용할 수 있다.(즉, 파라미터를 업데이트 하기 위해서는 그레디언트 벡터를 메모리에 저장시킬 필요가 있다는 것)