들어가기에 앞서
마지막 2734 드럼통 쌓기 문제를 제외하면 푸는데에 그렇게 어려움이 들지 않았다. 그리고 드럼통 쌓기 문제 역시 기하 문제여서 수학적 지식의 부족으로... 풀기가 어려웠던 거였지 원리만 알면 그렇게 어렵지 않았던 것 같다.
벌써 9주차인데 이제 슬슬 개강을 앞에두고 몸이 바빠지면서 대학원 생활도 힘들어지는 것 같다 ㅠ
11060 - 점프점프

처음에 BFS로 구현했다가 바로 시간초과로 혼이 나버렸다.
그래서 더 간단하게 할 수 있나보다라는 것을 알았고, 그림과 같은 원리로 동작한다.
visit 배열과 입력 배열 arr 두 개를 준비한다. visit[0] = 0으로 세팅한뒤 arr[0]에서 움직일 수 있는 칸들의 visit 배열을 채운다. 이때 visit[0] + 1의 값이 된다. 이것은 visit[0]에서 한번 더 움직여서 갈 수 있는 다음 칸이라는 것을 의미한다.
이 원리는 3번에 나와있다. 그리고 추가적으로 더 작은 횟수만에 해당 칸에 도달해야하므로, min()을 통해 현재 해당 칸에 들어가있는 값보다 작은 값일 때만 visit 배열을 갱신하도록 한다.
=> 지금 적으면서 생각해보니 어짜피 이미 방문한 칸은 더 작은 횟수만에 도달한 것이므로 딱히 확인할 필요가 없는 것 같다...
#include <iostream>
#include <memory.h>
#include <algorithm>
using namespace std;
int N;
int arr[1000];
int visit[1000];
int main() {
fill(&visit[0], &visit[1000], 2000);
cin >> N;
for (int i = 0; i < N; i++)
cin >> arr[i];
visit[0] = 0;
for (int i = 0; i < N; i++) {
int range = arr[i];
for (int j = 1; j <= range; j++) {
visit[i + j] = min(visit[i+j], visit[i] + 1);
}
}
if (visit[N - 1] == 2000)
cout << -1 << '\n';
else
cout << visit[N - 1] << '\n';
}1992 - 쿼드 트리
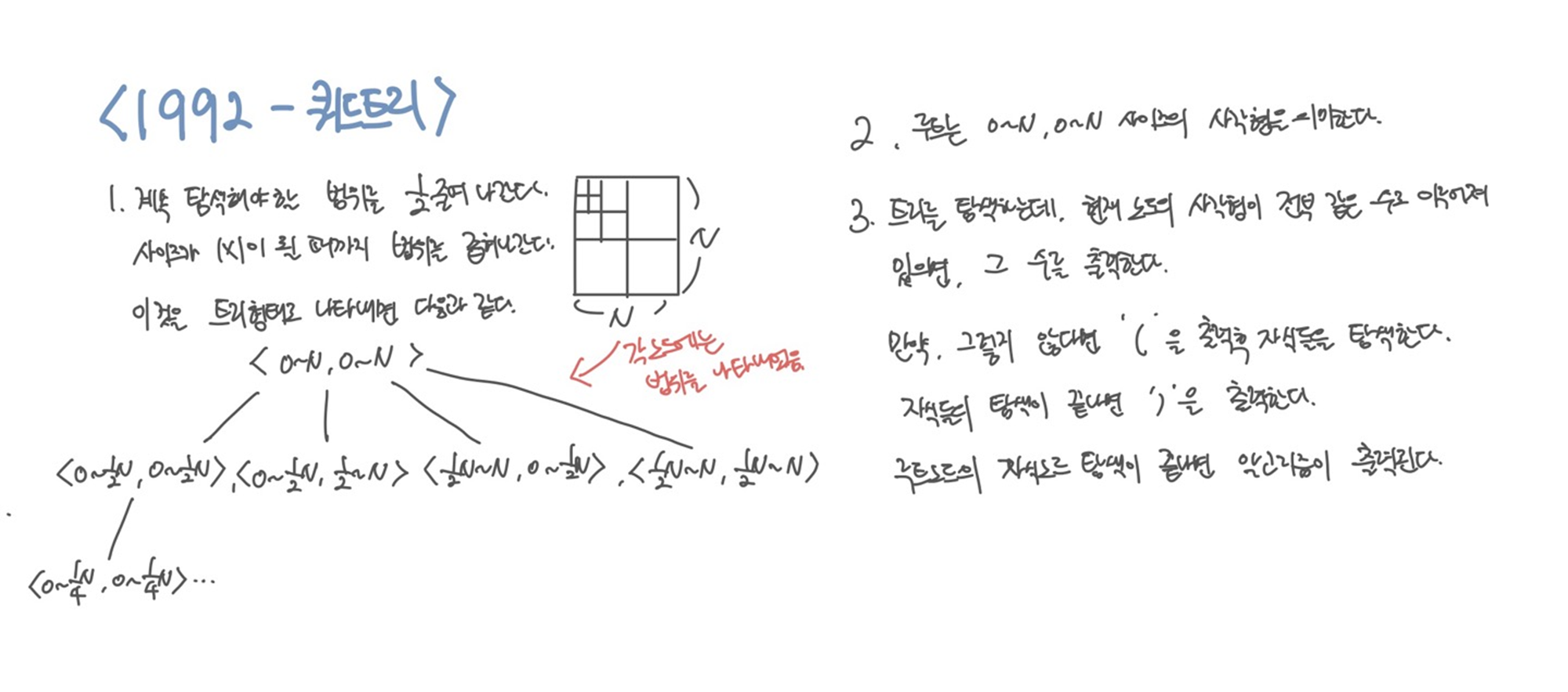
말 그대로 자식 노드를 네 개를 갖는 트리의 형태를 띈다. 현재 노드의 자식 노드는 순서대로 왼쪽위, 오른쪽위, 왼쪽아래, 오른쪽아래 부분의 사각형을 나타낸다. 그림에서 1을 참고하면 된다. 각 노드에는 해당 사각형이 나타내는 범위를 나타내고 있다.
루트부터 자식노드를 탐색한다. 이때, 현재 노드에 적혀있는 범위의 수가 0 또는 1로 전부 동일하다면 압축가능하기 때문에 해당 수를 출력한다.
만약 그렇지 않다면 '('를 출력하고 자식 노드들을 탐색한다. 마찬가지로 자식 노드는 왼쪽 자식부터 탐색하며 자식 노드에 적혀있는 범위의 숫자들이 0 또는 1로 모두 동일한 경우 해당 숫자를 출력하고, 그렇지 않다면 다시 자식 노드를 탐색하는 과정을 거친다. 자식 노드들의 탐색이 끝나면 ')'을 출력한다.
루트 노드의 자식노드 탐색이 끝나면 알고리즘이 종료된다.
#include <iostream>
#include <vector>
using namespace std;
int N;
int map[64][64] = { 0, };
bool check(int x1, int x2, int y1, int y2) {
int cnt = (x2 - x1) * (y2 - y1);
int sum = 0;
for (int i = x1; i < x2; i++) {
for (int j = y1; j < y2; j++) {
sum += map[i][j];
}
}
if (sum == 0 || sum == cnt)
return true;
else
return false;
}
void make_quad_tree(int start_x, int end_x, int start_y, int end_y) {
if (end_x - start_x == 1) {
cout << map[start_x][start_y];
}
else {
if (check(start_x, end_x, start_y, end_y)) {
cout << map[start_x][start_y];
}
else {
cout << '(';
int med_x = (int)(start_x + end_x) / 2;
int med_y = (int)(start_y + end_y) / 2;
make_quad_tree(start_x, med_x, start_y, med_y);
make_quad_tree(start_x, med_x, med_y, end_y);
make_quad_tree(med_x, end_x, start_y, med_y);
make_quad_tree(med_x, end_x, med_y, end_y);
cout << ')';
}
}
}
int main() {
cin >> N;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
scanf("%1d", &map[i][j]);
}
}
make_quad_tree(0, N, 0, N);
}5549 행성탐사

이 문제는 심플하다. 합을 저장해두는 2차원 어레이의 i,j에는 0,0에서 i,j까지의 합을 가지고 있으면 된다. 이처럼 합을 저장하기 위해서는 1주차 풀이 때 풀었던 문제를 참고하면 된다.
다음으로는 정글과 바다에 대해서만 합을 저장한다. 이 이유는 5번에서 설명한다.
참, c++에서 cin 그리고 cout을 사용하면 시간초과가 난다. 그래서 나같은 경우 scanf("%1s")와 printf()를 사용했더니 해결되었다.
얼음 수는 5번에서와 같이 구해야하는 범위의 칸수 - 정글 수 - 바다 수를 빼면 나머지 칸이 전부 얼음 칸 수이므로 따로 저장할 필요가 없다!!
#include <iostream>
#include <vector>
using namespace std;
int N, M, K;
char map[1001][1001] = { 0, };
int dpj[1001][1001] = { 0, };
int dpo[1001][1001] = { 0, };
int main() {
cin >> N >> M;
cin >> K;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= M; j++) {
scanf("%1s", &map[i][j]);
dpj[i][j] = dpj[i][j - 1] + dpj[i - 1][j] - dpj[i - 1][j - 1];
dpo[i][j] = dpo[i][j - 1] + dpo[i - 1][j] - dpo[i - 1][j - 1];
if (map[i][j] == 'J') {
dpj[i][j] += 1;
}
else if (map[i][j] == 'O') {
dpo[i][j] += 1;
}
}
}
int x1, y1, x2, y2;
int cnt, answerj, answero, answeri;
for (int i = 0; i < K; i++) {
scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
cnt = (x2 - x1 + 1) * (y2 - y1 + 1);
answerj = dpj[x2][y2] - dpj[x2][y1 - 1] - dpj[x1 - 1][y2] + dpj[x1 - 1][y1 - 1];
answero = dpo[x2][y2] - dpo[x2][y1 - 1] - dpo[x1 - 1][y2] + dpo[x1 - 1][y1 - 1];
answeri = cnt - answerj - answero;
printf("%d %d %d\n", answerj, answero, answeri);
}
}2734 - 드럼통 쌓기
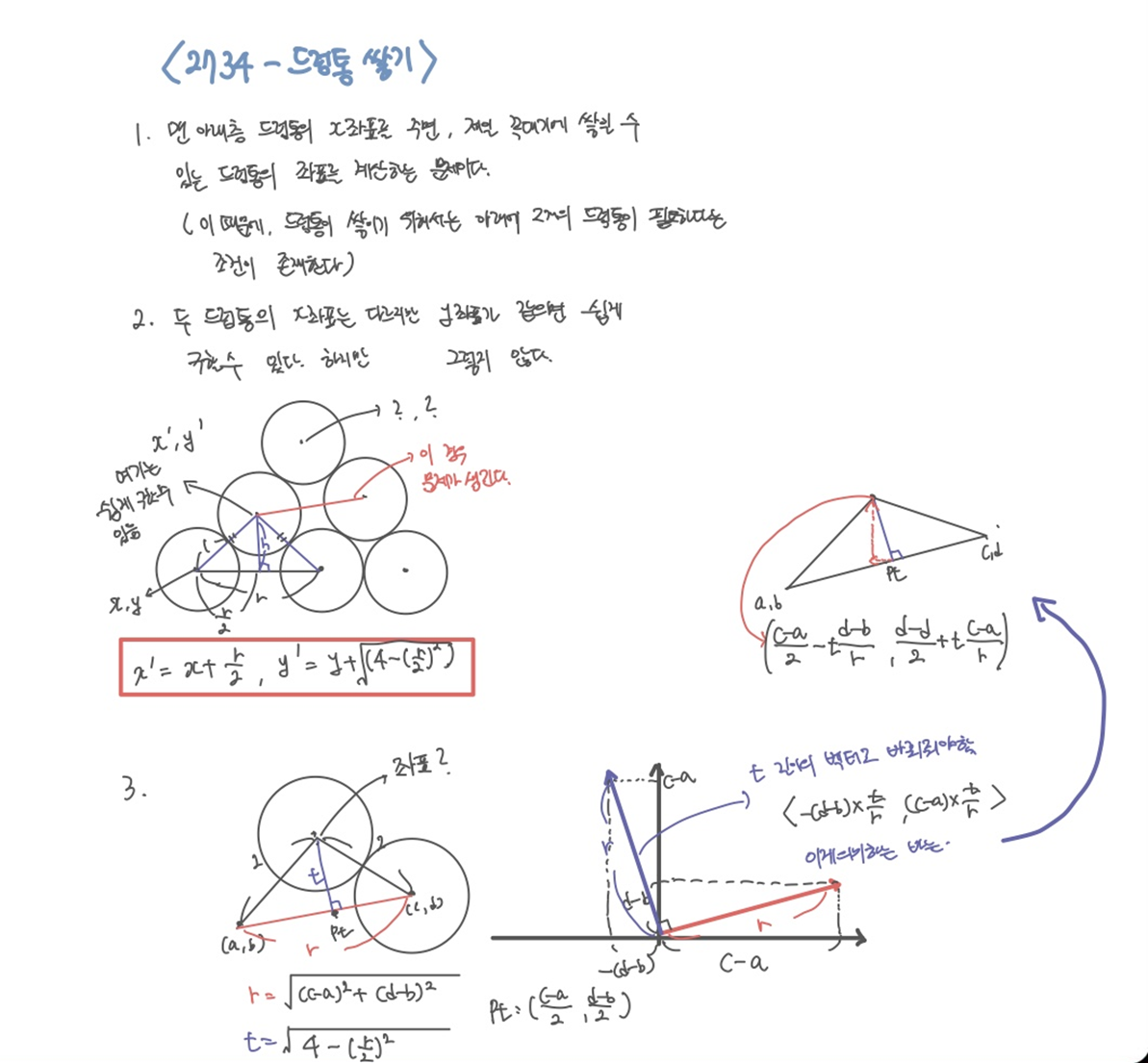
기하 문제,,, 다시는 보지말자
3번 과정만 잘 이해하면 된다.
우리는 r길이의 빨간 직선에 수직인 보라색 직선을 구해야한다. 그리고 t길이의 보라색 직선을 나타내는 벡터를 구한다면 r의 중점 pt를 기준으로 해당 벡터 값 만큼 이동해서 위에 쌓인 드럼통의 좌표를 알 수 있다.
자 차근차근 접근해보자.
먼저 우리는 pt의 좌표를 알 수 있다.(그림 참고)
r의 길이도 알 수 있다. -> 피타고라스 정리! 우리는 어른이니까!!
t의 길이도? 당연히 알 수 있다 -> 마찬가지
그러면 r 길이의 벡터는 오른쪽 좌표평면에 그려놓은 것과 같다. <c-a, d-b>
그렇다면 r에 수직이면서 길이가 r인 벡터를 구할 수 있다. <-(d-b), c-a>
그러면 구한 이 벡터를 t길이로 바꿔주기 위해 양쪽에 t/r을 곱한다.
<-t/r*(d-b), t/r * (c-a)>
그것이 의미하는 바는 r을 수직이등분하는 선과 r이 만나는 점 pt를 0,0으로 생각했을 때, 앞에서 구한 벡터의 사이즈만큼 이동하면 위에 쌓인 드럼통의 좌표를 구할 수 있다.
그래서 위에 쌓인 드럼통의 x 좌표는 pt의 x좌표 - t/r * (d-b) 이며,
y 좌표는 pt의 y좌표 + t/r * (c-a) 가 된다.
이걸 잘 이해할 수 있었으면 좋겠다. 나도 수학적으로 많이 부족하기에 설명을 잘한 것 같지는 않다...
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int T, N;
pair<double, double> center[10];
pair<double, double> answer;
void find_top(int size) {
if (size == 1) {
answer = center[0];
}
else {
pair<double, double> temp[10];
for (int i = 0; i < size - 1; i++) {
double a = center[i].first;
double b = center[i].second;
double c = center[i + 1].first;
double d = center[i + 1].second;
double r = sqrt(pow(c - a, 2) + pow(d - b, 2));
double t = sqrt(4 - pow(r / 2, 2));
double nx = (a + c) / 2 - (t * (d - b) / r);
double ny = (b + d) / 2 + (t * (c - a) / r);
temp[i] = make_pair(nx, ny);
}
for (int i = 0; i < size - 1; i++) {
center[i] = temp[i];
}
find_top(size - 1);
}
}
int main() {
scanf("%d", &T);
double input;
for (int i = 0; i < T; i++) {
cin >> N;
for (int j = 0; j < N; j++) {
cin >> input;
center[j] = make_pair(input, 1.0);
}
find_top(N);
printf("%.4f %.4f\n", answer.first, answer.second);
}
}소감
기하야 다시는 만나지 말자. 이번에는 그래도 고민하느라 꽤 즐거웠는데, 담엔 너한테 그렇게 애정을 못쏟겠어 ㅎㅎ
