[7주차] 백준 BoJ c++ 풀이 (2644, 2313, 17144, 13274)

개발자가 되기위한 힘겨운 사투 w.시현·2024년 2월 17일

boj 백준

알고리즘

목록 보기

10/13

들어가기에 앞서,,

실력이 상승되었는지는 모르겠으나 이번주 문제는 정말정말 쉽게 풀었다. 아이디어들도 되게 심플했고, 구현도 그렇게 어렵다고 느끼지 못했던 것 같다!! 코테도 이렇게 다 심플하면 얼마나 좋을까....

solved.ac에서는 내가 풀었던 문제들의 유형에 대해 내가 얼마나 잘 대비하고 있는지를 대략 보여주는데, 그리디나 문자열 관련 문제를 많이 풀어보지 못했다는 것을 알 수 있었다.

지금은 스터디에서 문제를 계속 랜덤하게 고르고 있기 때문에 당장 어떻게 할 방법은 없지만 계속 풀다보면 자연스럽게 올라가지 않을까?? 싶다

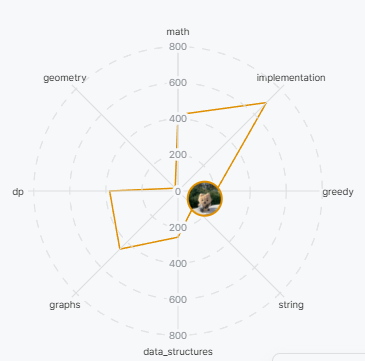
(구현은 별로 안풀었는데 왜 높은건지 잘 모르겟다... 에잇, 구현 싫어!!)

2644 - 촌수계산

이전에 풀었던 문제인데, 다른 사람들은 안풀었다고 해서 어짜피 오래전에 풀었던 문제라 재도전을 해보았다.

예전에 풀었는데 지금은 못풀까봐 조마조마했지만 실버급 문제답게 바로 해결책을 찾을 수 있었다.

먼저 관계를 입력받아서 그래프 형태로 저장한다. 그리고 촌수를 계산할 a, b를 입력받은 뒤, a에서 bfs 또는 dfs를 돌린다. 결과적으로 a에서 b까지 도달할 수 있다면 몇번만에 도달했는지를 출력하고 도달하지 못했다면 -1을 출력하면 된다.

#include <iostream>
#include <vector>
#include <queue>
#include <memory.h>

using namespace std;

int N, a, b, m;
vector<int> graph[100];
int visit[100];

queue<pair<int, int>> q;

void bfs(int start) {
	q.push(make_pair(start, 0));
	visit[start] = 0;

	while (!q.empty()) {
		int cn = q.front().first;
		int depth = q.front().second;
		q.pop();

		int nn;
		for (int i = 0; i < graph[cn].size(); i++) {
			nn = graph[cn][i];
			if (visit[nn] == -1) {
				q.push(make_pair(nn, depth + 1));
				visit[nn] = depth+1;
			}
		}
	}
}

int main() {
	cin >> N;
	cin >> a >> b;
	cin >> m;
	int x, y;
	memset(visit, -1, sizeof(visit));
	for (int i = 0; i < m; i++) {
		cin >> x >> y;
		graph[x - 1].push_back(y - 1);
		graph[y - 1].push_back(x - 1);
	}
	bfs(a-1);
	cout << visit[b - 1] << '\n';
}

2313 - 보석 구매하기

이전에 풀었던 파일합치기, 행렬 연산과 비슷한 문제라고 생각하고 풀었다.

dp[i][j]에는 i부터 j까지의 합을 들고 있을 수 있다면 dp 배열을 채운 뒤, 가장 큰 부분합 부분의 i, j를 구할 수 있다.

만약 똑같은 부분이 있다면 j - i가 더 작고 (= 부분합을 이루는 수들의 수가 적고) i, j가 더 작은 녀석이 답이 된다.

즉, dp의 끝단부터 탐색을 하면, i, j가 더 작은 녀석이 항상 갱신될 수 있다!!

#include <iostream>
#include <vector>
#include <memory.h>
#include <algorithm>
#include <limits.h>
typedef long long ll;

using namespace std;

int N, L;
ll dp[1000][1000];
ll answer = 0;

vector<pair<int, int>> answer_arr;

void find_max_sum() {
	ll max_sum = LLONG_MIN;
	pair<int, int> points = make_pair(0, L + 1);
	for (int i = L-1; i >= 0; i--) {
		for (int j = i; j < L; j++) {
			if (i != j)
				dp[i][j] = dp[i][i] + dp[i + 1][j];
			if (max_sum < dp[i][j]) {
				max_sum = dp[i][j];
				points = make_pair(i, j);
			}
			else if (max_sum == dp[i][j]) {
				if (points.second - points.first >= j - i) {
					points = make_pair(i, j);
				}
			}
		}
	}
	answer += max_sum;
	answer_arr.push_back(points);
}

int main() {
	cin >> N;
	for (int i = 0; i < N; i++) {
		cin >> L;
		memset(dp, -1, sizeof(dp));
		for (int j = 0; j < L; j++) {
			cin >> dp[j][j];
		}
		find_max_sum();
	}
	cout << answer << '\n';
	for (int i = 0; i < N; i++) {
		cout << answer_arr[i].first+1 << " " << answer_arr[i].second+1 << '\n';
	}
}

이 문제의 경우 1차원 DP로 dp[idx]는 1~idx까지 만들 수 있는 부분합의 최대를 들고 있고, 최대가 갱신될 때마다 i, j를 따로 갱신하여 저장해놓는 식으로 풀 수 있다.

17144 - 미세먼지 안녕

구현 문제라서 보자마자 한숨을 탁! 내쉬었지만 다행히 그렇게 어렵지 않았다.

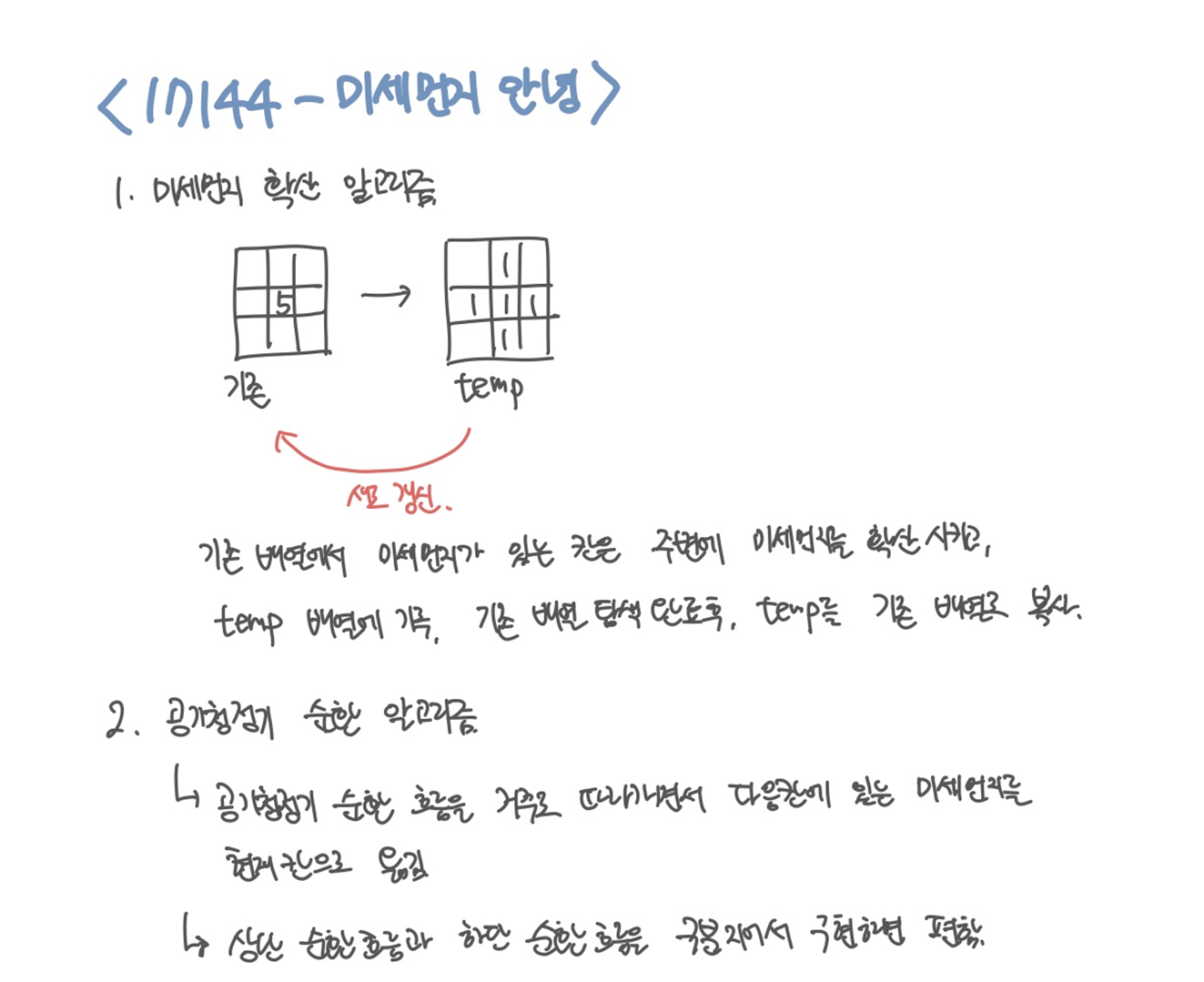
먼저 기존 배열에서 미세먼지가 들어있으면, 확산시킨다. 이 때 원래 배열을 건드리면 다음 칸에 확산된 미세먼지를 또 확산시킬 수 있기 때문에 temp 배열에 기록을 한다.

모든 칸의 미세먼지들을 다 확산시키면 temp 배열을 기존 배열로 복사해온다 (갱신).

미세먼지 확산이 완료되면 공기청정기 순환 파트를 구현한다.
너무 복잡하기 때문에 상단 순환과 하단 순환을 따로 함수로 구현했다.

편하게 순환을 관리하기 위해서는 공기의 순환 흐름의 역으로 추적하면서 다음 칸의 미세먼지를 현재칸으로 옮겨오면 된다.

코드는 아래와 같다.

#include <iostream>
#include <vector>

using namespace std;

int R, C, T;
vector<int> air;
int mise[50][50];

int dx[4] = { -1, 0, 1, 0 };
int dy[4] = { 0, 1, 0, -1 };

bool check(int x, int y) {
	if (x >= 0 && x < R && y >= 0 && y < C && mise[x][y] != -1)
		return true;
	return false;
}

void spread() {
	int temp[50][50] = { 0, };
	int nx, ny;
	for (int i = 0; i < R; i++) {
		for (int j = 0; j < C; j++) {
			if (mise[i][j] == -1)
				temp[i][j] = -1;
			if (mise[i][j] > 4) {
				int amount = (int)mise[i][j] / 5;
				int cnt = 0;
				for (int k = 0; k < 4; k++) {
					nx = i + dx[k];
					ny = j + dy[k];
					if (check(nx, ny)) {
						temp[nx][ny] += amount;
						cnt++;
					}
				}
				temp[i][j] += (mise[i][j] - amount * cnt);
			}
			else if (mise[i][j] < 5 && mise[i][j] > 0)
				temp[i][j] += mise[i][j];
		}
	}
	
	for (int i = 0; i < R; i++) {
		for (int j = 0; j < C; j++)
			mise[i][j] = temp[i][j];
	}
}

void top_air_cleaner() {
	for (int i = air[0] - 1; i > 0; i--)
		mise[i][0] = mise[i - 1][0];
	for (int i = 0; i < C - 1; i++)
		mise[0][i] = mise[0][i + 1];
	for (int i = 0; i < air[0]; i++)
		mise[i][C - 1] = mise[i + 1][C - 1];
	for (int i = C - 1; i > 1; i--)
		mise[air[0]][i] = mise[air[0]][i - 1];
	mise[air[0]][1] = 0;
}

void bottom_air_cleaner() {
	for (int i = air[1] + 1; i < R-1; i++) {
		mise[i][0] = mise[i + 1][0];
	}
	for (int i = 0; i < C - 1; i++) {
		mise[R - 1][i] = mise[R - 1][i + 1];
	}
	for (int i = R - 1; i > air[1]; i--) {
		mise[i][C - 1] = mise[i - 1][C - 1];
	}
	for (int i = C - 1; i > 1; i--) {
		mise[air[1]][i] = mise[air[1]][i - 1];
	}
	mise[air[1]][1] = 0;
}

void run_air_cleaner() {
	top_air_cleaner();
	bottom_air_cleaner();
}

int main() {
	cin >> R >> C >> T;
	int input;
	for (int i = 0; i < R; i++) {
		for (int j = 0; j < C; j++) {
			cin >> input;
			mise[i][j] = input;
			if (input == -1)
				air.push_back(i);
		}
	}
	
	int answer = 0;
	for (int i = 0; i < T; i++) {
		spread();

		run_air_cleaner();
	}
	for (int i = 0; i < R; i++) {
		for (int j = 0; j < C; j++) {
			if (mise[i][j] > 0)
				answer += mise[i][j];
		}
	}
	cout << answer << '\n';
}

13274 - 수열

이 문제가 조금 어려울 수 있는데, 정렬된 수열이 있을 때 L부터 R까지 양수 X를 더할 때와 음수 X를 더할 때를 각각 나누어 생각했다.

1) 양수 X의 경우
L부터 R까지의 수는 무조건!! 1~L-1까지의 수보다 크다. 그래서 1~L-1의 수들은 순서를 고정하고 R+1~end까지 수들과 각각 비교하여 더 작은 수를 차곡차곡 담는다.

2) 음수 X의 경우
L부터 R까지의 수는 무조건!! R+1보다 end까지의 수보다 작다. 그래서 1~L-1의 수들과 각각 비교하여 더 작은 수들을 차곡차곡 담는다. L~R그리고 1~L-1의 모든 수들이 정렬되어 수열에 담기면 R+1부터 N까지의 수들은 순서를 그대로 담는다.

이 과정을 N번 반복하면, 정답이 나온다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int N, K, L, R;
long long X;
vector<long long> arr;

void sorting() {
	vector<long long> temp;
	/*
		temp 벡터에 push_back으로 일일히 넣어주는 것보다,
		temp 벡터를 n개의 0으로 채우고,
		값을 temp[i] = arr[j]와 같은 식으로 바꿔주는 것이
		시간초과 해결에 도움이된다.
	*/
	temp.assign(N, 0);
	if (X > 0) {
		int point1 = L - 1, point2 = R;
		int idx = L - 1;
		for (int i = 0; i < L - 1; i++) {
			temp[i] = arr[i];
		}
		while (point1 < R && point2 < N) {
			if (arr[point1] + X < arr[point2]) {
				temp[idx++] = arr[point1++] + X;
			}
			else {
				temp[idx++] = arr[point2++];
			}
		}
		if (point1 == R) {
			for (int i = point2; i < N; i++) {
				temp[idx++] = arr[i];
			}
		}
		else if (point2 == N) {
			for (int i = point1; i < R; i++) {
				temp[idx++] = arr[i] + X;
			}
		}
		for (int i = 0; i < N; i++) {
			arr[i] = temp[i];
		}
	}
	else if (X < 0) {
		int point1 = 0, point2 = L - 1;
		int idx = 0;
		while (point1 < L-1 && point2 < R) {
			if (arr[point1]< arr[point2] + X) {
				temp[idx++] = arr[point1++];
			}
			else {
				temp[idx++] = arr[point2++] + X;
			}
		}
		if (point1 == L-1) {
			for (int i = point2; i < R; i++) {
				temp[idx++] = arr[i] + X;
			}
		}
		else if (point2 == R) {
			for (int i = point1; i < L-1; i++) {
				temp[idx++] = arr[i];
			}
		}
		for (int i = R; i < N; i++) {
			temp[i] = arr[i];
		}
		for (int i = 0; i < N; i++) {
			arr[i] = temp[i];
		}
	}
}

int main() {
	cin >> N >> K;
	long long input;
	for (int i = 0; i < N; i++) {
		cin >> input;
		arr.push_back(input);
	}
	sort(arr.begin(), arr.end());
	for (int i = 0; i < K; i++) {
		cin >> L >> R >> X;
		sorting();
	}

	for (int i = 0; i < arr.size(); i++) {
		cout << arr[i] << ' ';
	}
}

이 문제의 경우 L부터 R의 원소들을 항상 먼저 1~L-1까지의 수와 비교하여 차곡차곡 수열에 담을 수 있다. 이후, 1~L-1의 수는 다 정렬되었는데 L부터 R의 수는 아직 정렬이 덜 되었다면 그 때는 R+1부터 end까지의 수들과 각각 비교하여 수열에 담는 식으로 풀 수 있다.

이러면 X가 양수인지 음수인지는 중요하지 않다.