수학 #2 [제2 코사인법칙 증명]

황재진·2022년 7월 12일

목록 보기

2/5

제2 코사인법칙은 앞으로의 증명에 아주 많이 사용하게될 법칙이므로 아주 중요합니다.

공식

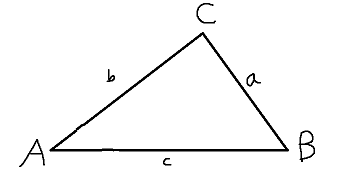
a^2=b^2+c^2 - 2bc×cosA

b^2=c^2+a^2 - 2ca×cosB

c^2=a^2+b^2 - 2ab×cosC

제2 코사인법칙을 증명하는 방법은 다양합니다.
제1 코사인법칙을 사용해 증명할 수도 있고, 피타고라스 정리를 사용해 증명할 수도 있습니다.
저는 피타고라스 정리를 사용해 증명해보겠습니다.

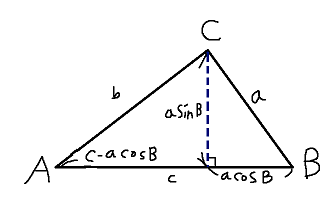
삼각형에 수직선을 긋고 수선들을 다음과 같이 정의했습니다.
피타고라스 정리를 사용하면 아래와 같은 식이 나옵니다.

b^2=(c-acosB)^2+a^2sin^2B

b^2=c^2-2cacosB+a^2cos^2B+a^ssin^2B

b^2=c^2-2cacosB+a^2(sin^2B+cos^2B)

위 식에서 $sin^2\theta+cos^2\theta=1$ 입니다.
이에 대한 증명은 아래에서 하도록 하겠습니다.
위 식에 1을 대입하면 코사인 공식이 나오게 됩니다.

b^2=c^2-2cacosB+a^2

b^2=a^2+c^2-2cacosB

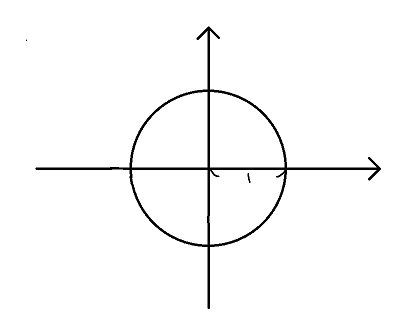
위 사진과 같이 반지름이 1인 단위원이 원점에 있다고 해보자.
저기에 삼각형을 하나 그려보자.

해당 삼각형의 빗변의 길이도 1이다.
그러면 밑변은 $cos\theta$ 이고 높이는 $sin\theta$ 가 된다.

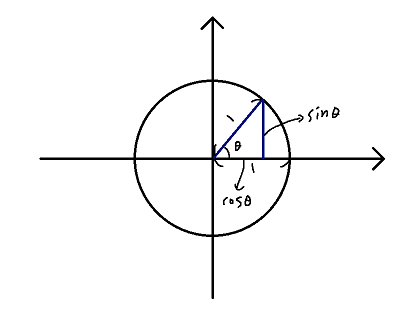
여기서 피타고라스 정리를 사용하면

sin^2\theta+cos^2\theta=1

이 나온다.

프로그래밍, 쉐이더 등 이것저것 다해보는 게임 개발자입니다