공식
삼각형 ABC의 세 각을 A, B, C라고 하고 그 대변을 a, b, c라 할 때
a=b×cosC+c×cosB
b=c×cosA+a×cosC
c=a×cosB+b×cosA
a를 구할 때 b와 cosC를 곱한 값에 c와 cosB를 곱한 값을 더해주는 방식이다.
증명
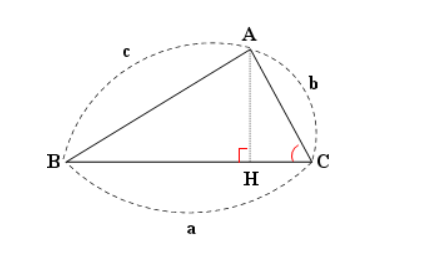
1. 예각일 때
C가 예각일 때의 증명

A에서 변 BC에 내린 수선의 발을 H라고 해보자.
삼각형 ABH에서
cosB=BH/c
c×cosB=BH
삼각형 ACH에서
cosC=CH/b
b×cosC=CH
결국 변 CH의 길이는 bcosC이고 변 BH의 길이는 ccosB이므로
a=b×cosC+c×cosB
이 식이 성립하게 된다.
2. 직각일 때
C가 직각일 때의 증명

C가 직각일 경우에는 보조선을 그을 필요가 없다.
cosC=cos90º=0
a는 변 BC이고, 변 BC는 ccosB이고 bcosC는 0이므로
a=b×cosC+c×cosB
이 식이 성립하게 된다.
3. 둔각일 때
C가 둔각일 때의 증명
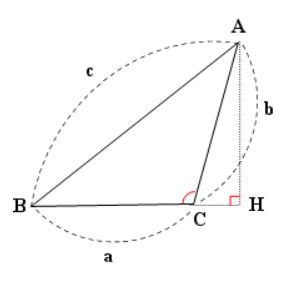
A에서 변 BC로 내린 수선의 발을 H라고 해보자.
BH와 CH의 길이를 구해보자
삼각형 ABH에서
cosB=BH/c
BH=c×cosB
삼각형 ACH에서
cos(180−C)=−cosC=CH/2
CH=b×−cosC
변 BH는 ccosB이고, 변 CH는 -bcosC이므로
a=c×cosB+b×cosC
식이 성립하게 된다.
cos(180−C)=−cosC
엄밀한 증명을 위해선 위 식이 성립함 또한 증명해야 한다.
코사인 그래프를 봐보자.
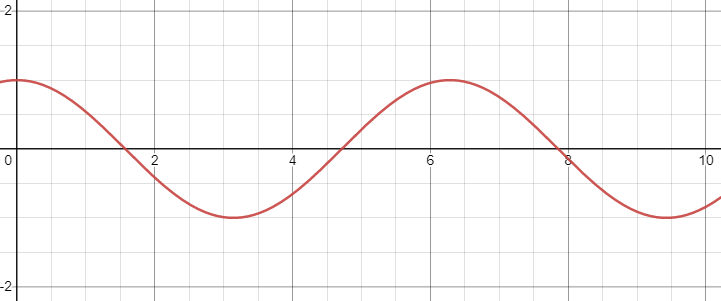
일반각에서의 180°는 π이다. 그러니 그래프를 0에서 π까지만 봐보자.
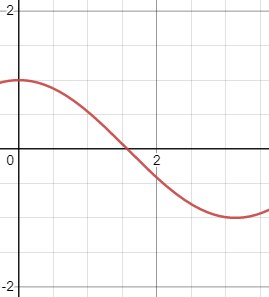
해당 그래프의 중간 지점에서 보면 기함수의 형태를 띈다.
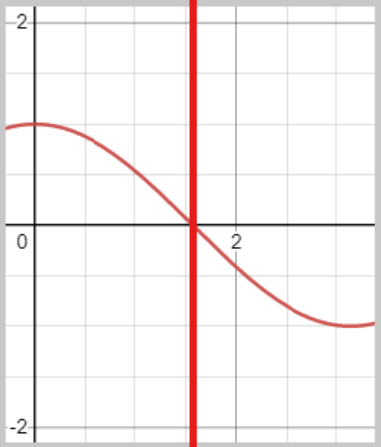
양쪽은 원점 대칭이 되므로 180 - C의 cos값은 C의 값에 음수를 붙인 값이 맞다.