수학 #3 [벡터의 내적 공식, 증명, 의미]

황재진·2022년 7월 14일

목록 보기

3/5

공식

$\vec{A}=(a_1,a_2)$ , $\vec{B}=(b_1,b_2)$ 인 두 벡터가 있다고 할 때

\vec{A} \ \bullet \vec{B}=||\vec{A}||\cdot||\vec{B}||\cdot cos\theta \\ = a_1b_1\cdot a_2b_2

벡터의 내적 공식은 두가지가 있으며, 두 벡터를 내적한 결과는 스칼라입니다.

위 두 식이 같음을 증명해보겠습니다.
해당 증명에는 제2 코사인법칙이 활용되니 제2 코사인법칙을 모르시는 분은 텍스트를 눌러 글을 읽고 와주시기 바랍니다.

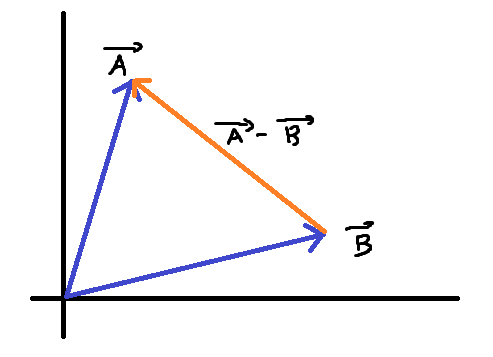
위 사진처럼 두 벡터 $\vec{A},\ \vec{B},\ (\vec{A}-\vec{B})$ 를 정의했다.
이를 코사인 법칙을 활용해 식을 표현하면

||\vec{A}-\vec{B}||^2=||\vec{A}||^2+||\vec{B}||^2-2||\vec{A}||\ ||\vec{B}||cos\theta

라고 표현할 수 있다.

$||\vec{A}||^2={a_1}^2+{a_2}^2$
$||\vec{B}||^2={b_1}^2+{b_2}^2$
$||\vec{A}-\vec{B}||=(a_1-b_1)^2-(a_2-b_2)^2$ 이므로

(a_1-b_1)^2={a_1}^2+{a_2}^2+{b_1}^2+{b_2}^2-2||\vec{A}||\ ||\vec{B}||cos\theta \\ {a_1}^2-2a_1b_1+{b_1}^2+{a_2}^2-2a_2b_2+{b_2}^2={a_1}^2+{a_2}^2+{b_1}^2+{b_2}^2-2||\vec{A}||\ ||\vec{B}||cos\theta

이를 정리하면

-2(a_1b_1 + a_2b_2)=-2||\vec{A}||\ ||\vec{B}||cos\theta

양변을 -2로 나누면

a_1b_1 + a_2b_2=||\vec{A}||\ ||\vec{B}||cos\theta

이렇게 같음이 증명되었다.

여기서부턴 주관적인 의견이 들어갈 수 있습니다.

내적에는 코사인이 들어간다. 즉, 두 벡터 사이의 각도가 작을수록 값이 크고, 클수록 값이 작아진다.
이는 두 벡터의 방향이 일치하는 정도를 나타낸다고 생각했다.

프로그래밍, 쉐이더 등 이것저것 다해보는 게임 개발자입니다