오늘 한 일

• 스프린트 챌린지
• 스프린트 복습

keyword :

• assert : 뒤의 조건이 True가 아니면 AssertError를 발생한다.
  (s2s1 스첼에 나오는 내용)
• label : 머신러닝(지도학습)의 label은 예측하고자 하는 대상, 곧 target을 가리킨다.

sprint wrap up :

• 지도학습 비지도 학습 차이
  레이블(label), 타겟 레이블이 있느냐 없느냐의 차이 ❓
  지도학습(supervised learning) : classification(분류), 회귀
  보통 지도학습을 이야기 하면 분류랑 회귀를 생각하면 됨(물론 세부로 파고들면 여러가지가 있겠지만 우선을 이렇게 생각)
  비지도 학습 : 클러스터링 (클러스터링의 종류에는 k-means 등등이 포함됨)

고객이 이 물건을 살것인가 사지 않을 것인가?
-> 분류 classification 살것, 사지 않을 것으로 분류하는 것이므로
어떤 물건을 사는 고객군을 찾고 싶다.
-> 클러스터링(비지도 학습)
군이 어떤 기준(label)을 가진 군인지 정해진건 아님. 우선 어떠한 군으로 분류한다는 느낌 만약 kmeans의 k가 5라면 5개의 군으로

1. 단순선형회귀 linear regression

• 기준모델이 필요한 이유 : 최소한의 성능을 보여주는 지표가 됨.'이것보다는 넘어야 한다'의 최소 기준이라고 생각하면 편하다.
  "얘, 모델을 만들었으면 솔직히 이것(기준모델)보단 잘해야지.."

• 평가지표 (evaluation metrics)
  분류 : 타겟의 최빈 클래스
  회귀 : 타겟 평균(중간값 등)
  시계열 : 이전 타임스탬프의 값
  참고 ) 이전 타임스탬프란? : 주식 값(바로 전에 거래됐던 값 / 자동차 gps 바로 전에 위치 했던 값등)

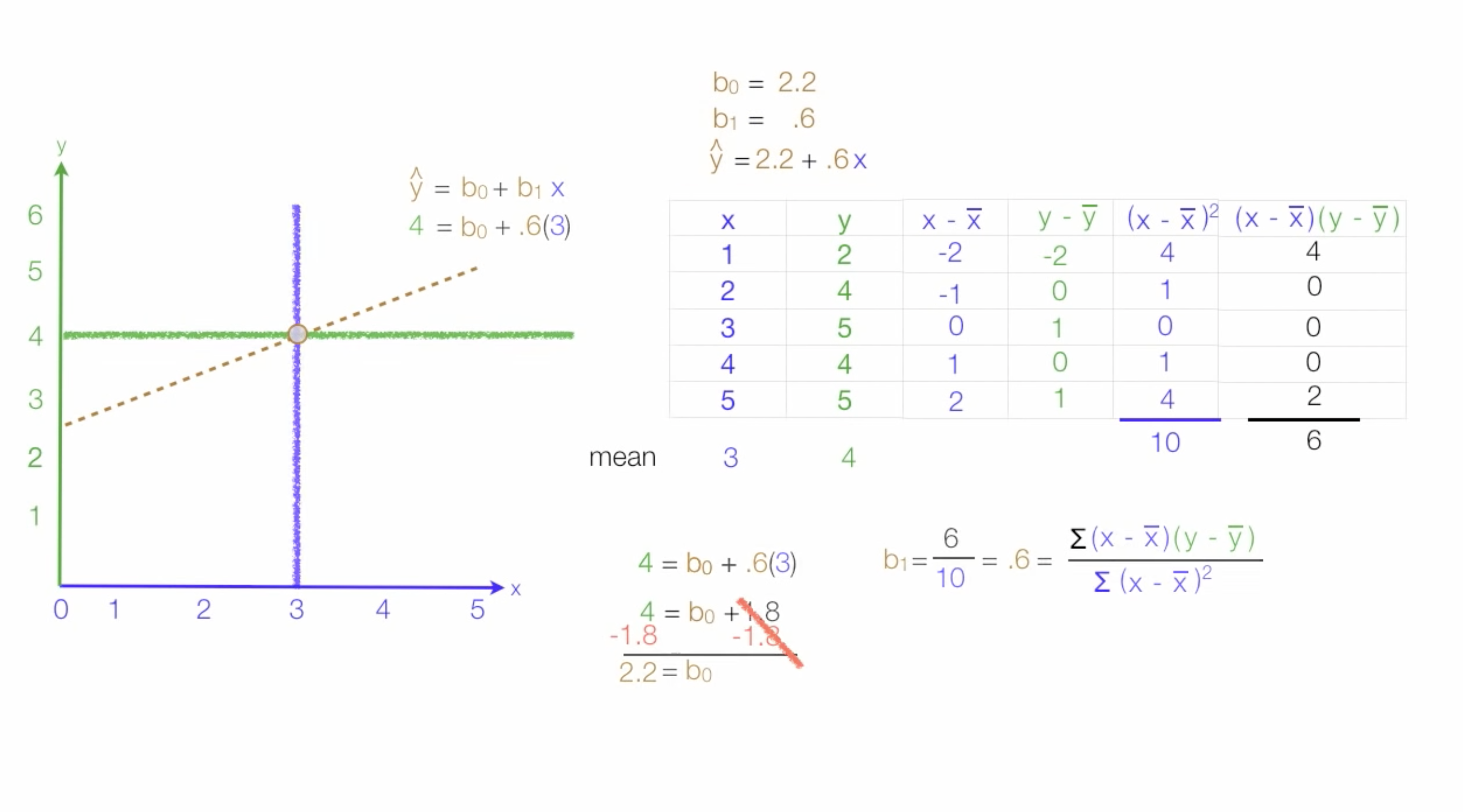
* 최소자승법

• 최소자승법이란 모델의 파라미터를 구하기 위한 대표적인 방법 중 하나
  모델과 데이터와의 잔차(residual^2) 제곱의 합을 최소화 하도록 모델의 파라미터를 구하는 방법
  

* 테이블 데이터(Tabular Data)

• 구성

1. Observations - 테이블의 행에 위치, 단일 데이터타입이여야 한다.
2. Variables - 테이블의 열에 위치, 여러가지 데이터타입이 포함 될 수 있다.
3. Relationship - 테이블과 테이블을 연결 (key 값을 이용한다)
   만드는 데이터가 이 테이블 데이터인지 앞으로 항상 확인

• mae의 장점
  스케일이 같아서 비교가 편하다. mse보다는 이상치에 덜 민감(더블링이 안되니깐!)

• rss(residual sum of squares) = sse(Sum of Square Error) ❓

• 선형회귀는 주어져 있지 않은 점의 함수값을 보간하여 예측하는데 도움을 줌

• 머신러닝 프로세스
  
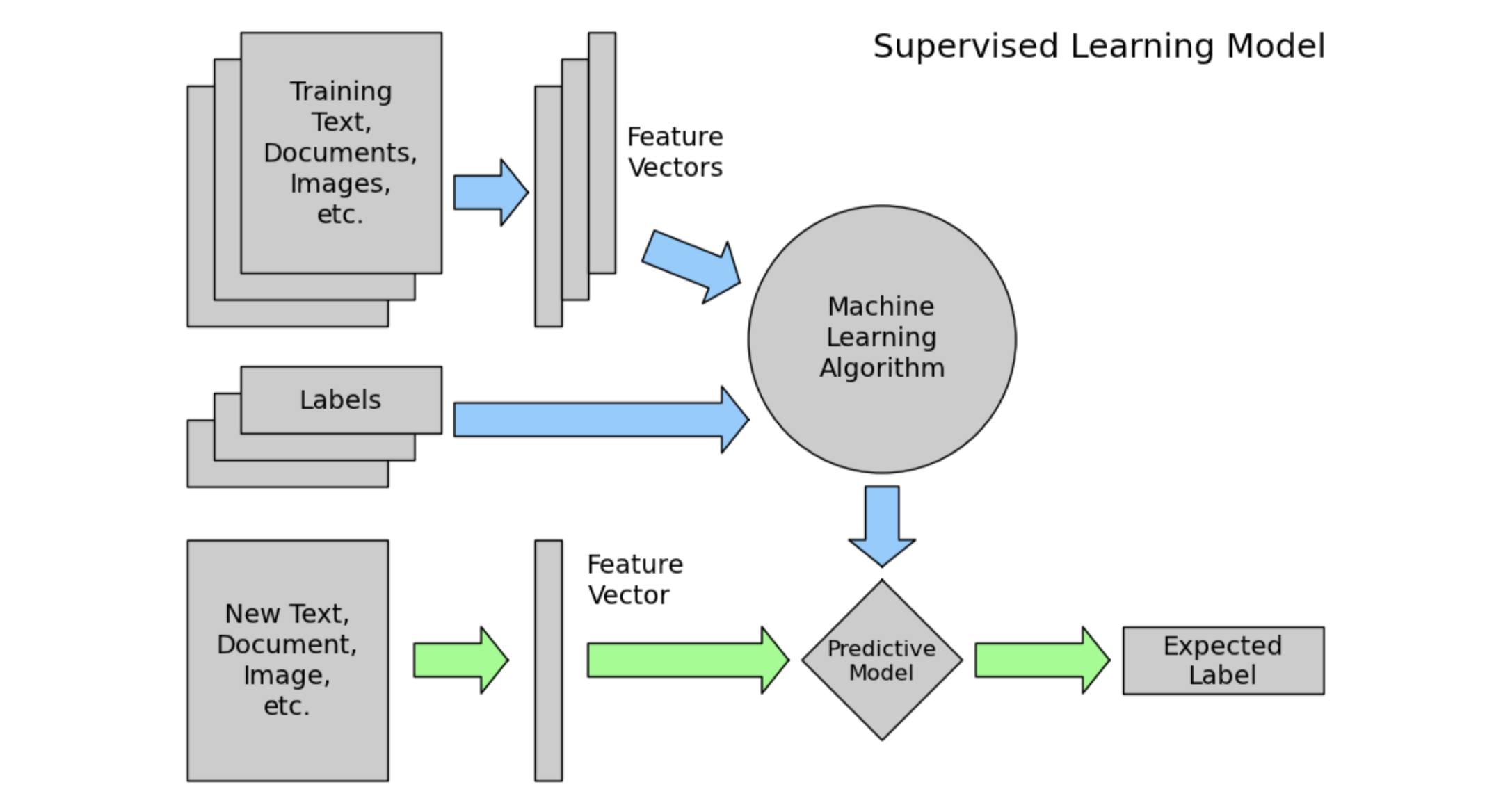
  파란색 : train
  초록색 : test

• 선형회귀가 가지고 있는 가장 큰 장점 : 회귀계수 해석이 쉽다!(수식만 봐도 너무 간단) 직관적으로 설명할 수 있다. (직관적 분석 가능) 그래서 선형회귀분석이라고도 한다.
  여기서 회귀계수 분석이란? 한 feature의 단위가 커질수록 target이 얼마나 변하는지, 어떻게 변하는지
  직관적으로 확인할 수 있다.

2. 다중선형회귀 multiple linear regression

• 단위 회귀에 비해 특성들이 늘어난 회귀

• 학습과 테스트 데이터를 분리하는 이유? 모델이 잘 만들어졌는지 (일반화가 잘되었는지) 확인하기 위해

• 선형회귀는 다른 ML 모델에 비해 상대적으로 학습이 빠르고 설명력이 강하다. 하지만 선형 모델의 이므로 과소적합(underfitting)이 잘 일어난다는 단점이 있다.

• 과적합/과소적합
  일반화가 잘된 모델은 과적합, 과소적합 둘다 아님.

• 편향분산 트레이드 오프와 일반화 관점을 잘 연결해서 알아야함! ❓

• 결정계수 r^2가 1에 가깝다는 것은? 모델의 설명력이 높다. 잘 fitting 되었다.
  r^2은 0~1사이의 값이 나옴

• note에서 mse, mae쪽을 보면 수식이 있는데 그런걸 ‘LaTex(수식문법)’이라고 함.(아래 사진 참조)
  평가지표는 다같이 보고 확인하는게 좋겠죠?
  

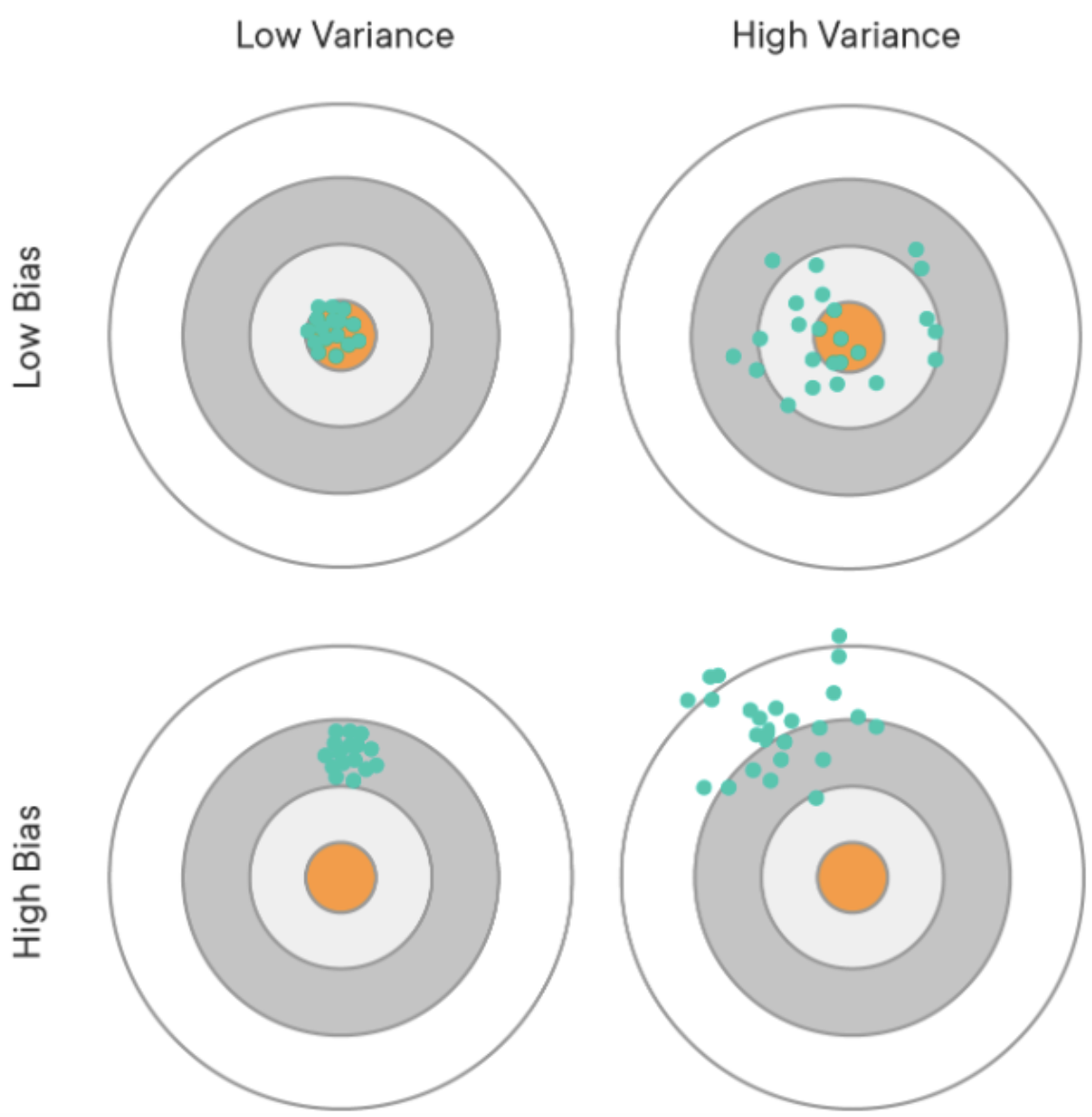
• 분산이 높은 경우는 일반화를 잘 못하는 경우 즉 과적합 ❓

• 편향이 높은 경우는 모델이 학습 데이터에서 특성과 타겟 변수의 관계를 파악하지 못함 과소적합 ❓

• 그 밑의 그림을 보면 파랑 - 트레인 / 초록 - 테스트
  🤚 이 그림을 보고 설명하는 연습을 해봤으면 좋겠다.
  
  
  

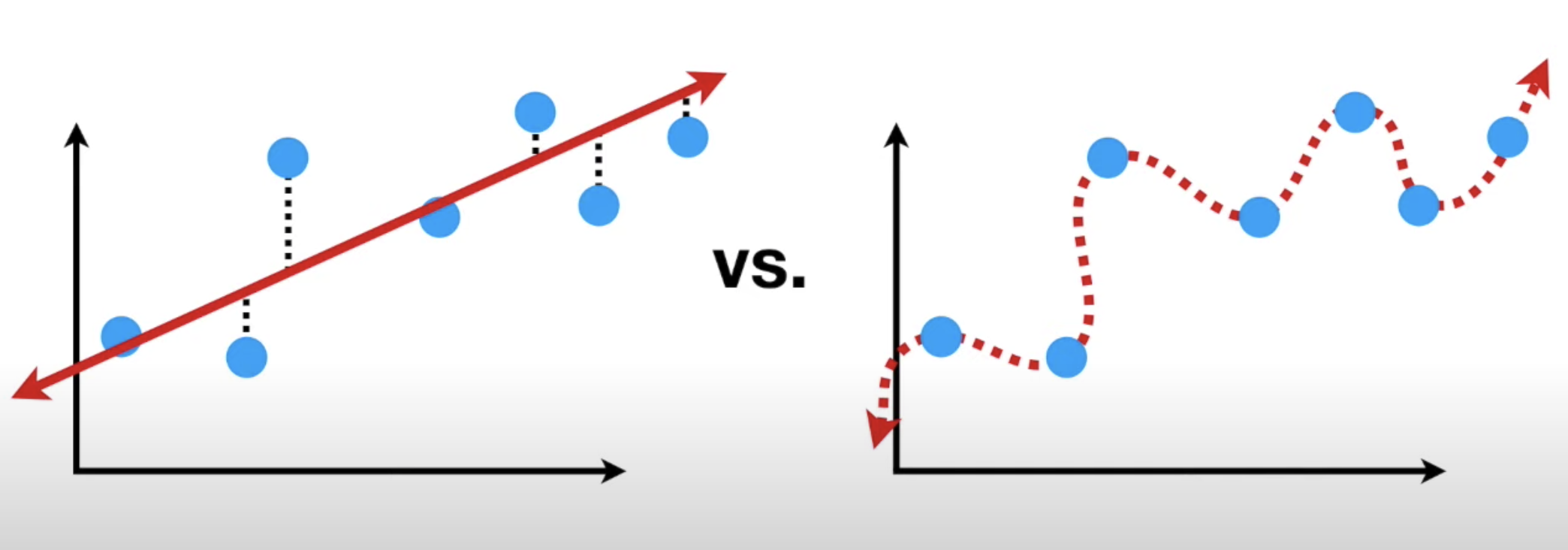
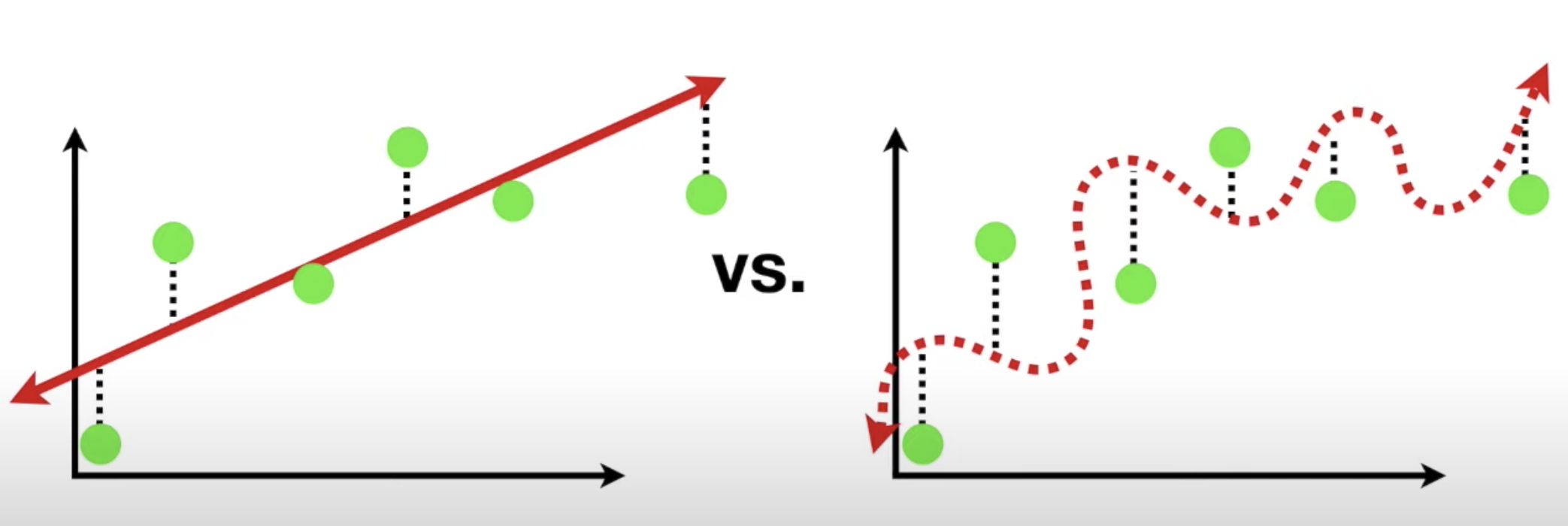
3. ridge회귀

• 원핫인코딩은 아주 좋은 인코딩 방법이다! 범주형 변수값들을 0과 1로만 바꾼다. 따라서 원핫인코딩을 하면 변수들의 갯수가 늘어난다. (범주의 갯수만큼) 원핫인코딩할때는 category encoders를 쓰는 것을 추천!! (싸이킷런에도 있지만 지금은 카테고리 인코더를 추천함)

• 원핫인코딩안에도 종류가 여러가지 있다. (더미코딩이라던가, 원핫인코딩이라던가...)
  그런데 우선 흔히 아는 그 원핫인코딩만 알고 있으면 됨

• Feature selection 특성선택
  특성선택은 특성공학인가? ㄴㄴ 특성공학안에 특성선택이 들어가는 것 (특성공학은 아주 방대한 분야이다)
  특성선택의 기법에는 selectKBest 등이 있다. 이 외에도 많으니깐 한번씩 알아보면 좋을 것 같다.
  특성선택

* ridge 회귀의 정규화

정규화를 하는 이유는 과적합을 해결하기 위해서이다. 근데 정규화를 너무 쎄게 하면 과소적합이 되어버린다.
참고) Ridge 회귀는 이 편향을 조금 더하고, 분산을 줄이는 방법으로 정규화(Regularization)를 수행합니다. 여기서 말하는 정규화는 모델을 변형하여 과적합을 완화해 일반화 성능을 높여주기 위한 기법을 말합니다.

• 릿지회귀는 분산편향트레이드오프 개념을 따르는가? yes
  모델에 편향을 약간 더해서 분산을 많이 줄어들게 할 수 있다.❓
  릿지회귀에는 람다라는 패널티 값이 있다.
  람다라는 패널티 값을 크게 잡으면 하이바이어스 편향이 많이 추가되어 과소적합이 됨.
  릿지회귀를 이용하면 학습성능이 많이 올라가나요? no 일정 이상으로 가면 떨어져요 ❓ (복습 필요)

• 릿지회귀에 릿지cv를 사용한 이유? 적절한 알파(람다값)를 찾으려고

• ‘최종모델’을 강조한 이유? ❓(다시 읽어보기)
  test셋은 한번만 사용할 수 있어서!
  가장 적절한 람다값을 적용한 모델을 테스트 데이터셋에 사용하므로

• 실무팁! 검증 다끝나고 모델을 만들어서 회사에서 서비스를 할때) 테스트를 했던 애들도 그냥 영끌해서 학습시켜서(아깝자너..) 모델을 최애애애ㅐㅐ애애대한 개선시킬 수 있다. (비즈니스적 관점에서 봤을때 test데이터도 학습에 쓰일 수 있는 것이다.)

4. logistic 회귀

• 훈련, 검증, 테스트 세트는 머신러닝에서 특별한 일이 없는 한 항상 세개로 나눠서 할 것임

• 검증세트는 하이퍼파라미터 튜닝을 위해 쓴다. 모델의 하이퍼파라미터를 살짝 바꿔도 모델은 다른 모델이 된다. 이렇게 달라진 모델을 비교하기 위해서 검증세트를 쓴다.
  (릿지회귀에서도 람다 1이랑 람다3은 서로 다른 모델이다)

• 로지스틱 회귀가 회귀모델인가요? ㄴㄴ 분류모델
  선형회귀 모델에 시그모이드를 넣어서 구부린것
  그래서 p(x)식을 보면 시그모이드 함수 안에 선형회귀 식이 들어가있다.
  🤚 식 캡쳐해서 추가하기

• odds를 이용하면? 선형회귀처럼 되어서 회귀 계수를 얻을 수 있다. 그니깐! 로지스틱 회귀는 분류모델인데 선형회귀의 장점을 가지고 있다고 할 수 있다. 🤚 로짓변환과 무슨 관계가 있는지 살펴보기
  참고) 로짓변환은 비선형 형태인 로지스틱회귀에 로그함수를 취해 선형형태처럼 만들어 회귀계수를 해석하는 방법이다.

• note4 캐글에 꼭 제출 해보기!!!! 다른 스프린트할때 캐글 챌린지 할 것이기 때문에 캐글에 익숙해지는게 좋음.

• 내가 생각한 머신러닝 프로세스
  주어진 데이터 : 집값과 집과 관련된 피쳐들
  step 1 : 어떤 문제를 풀려고 하나요? -> 집값을 예측하는데 있어서 어떤 피쳐의 영향이 큰가 적은가 +인가 -인가? 🤚 피쳐와 타겟의 관계를 볼수 있는 지표같은 것이 있는가? 예상) 상관관계 분석 corr, 피쳐 select(KBestSelect?)
  step 2 : train, validation, test데이터로 나눠주고 용도에 맞는 모델에 train data를 fit
  step 3 : validation으로 평가지표들을 살펴보며 더 알맞은 모델을 찾아보거나 파라미터를 조정한다.
  step 4 : 마지막 테스트!

내일 할 일

• 오늘 TIL을 다시 살펴보며 (note와 함께) 정리하기
• 4개 노트 정리하면서 '분산편향트레이드오프 '같은 중요하면서도 잘 와닿지 않는 개념은 따로 적어두었다가 블로그에 따로 정리
• [] 노트 정리가 끝나면 이번주 TIL keyword를 보며 개념 되새김. 또한 빠진 개념이 있는지 살펴보기. 만약 빠진 개념이 있으면 내일 TIL에 정리하기
• [] 내일 모레 할 일 : 도전문제 풀어보기

🐹
숲을 볼줄 알아야 함! 뭘하고 있는지에 대한 탐구 계속 해야함. 모르는 것과 아는 것의 구별, 모르는 것은 찾는 법을 알것, 질문하는 법을 알것

지금까지 내가 생각한 블로그 운영 방법은 다음과 같다.

TIL을 기본으로...

📎 keyword : 새로 배운 개념, 단어, 나중에 한번 다시 보고 싶은 새로운 용어 등을 적는다.
💾 sprint wrap up : 하나의 스프린트가 끝나고, 랩업 시간에 들은 것을 필기. 나중에 이 내용을 바탕으로 블로그에 따로 정리할 것이나, 빠진 개념을 don't miss에 적은다.
💎 dont't miss : 
🎸 etc : Q&A시간에 들은 유용한 질문 답변이나, 나중에 쓸 것 같은 코드를 적는다.

개선할 점이 있으면 하다가 유연하게 개선해 나가면 될 것 같다!