(6549) 히스토그램에서 가장 큰 직사각형 (Java)

문제

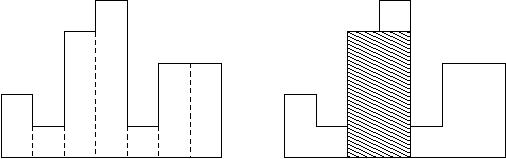
히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.

히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.

입력

입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.

출력

각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.

예제 입력 1

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

예제 출력 1

8
4000

출처

Contest > University of Ulm Local Contest > University of Ulm Local Contest 2003 H번

문제를 번역한 사람: baekjoon
어색한 표현을 찾은 사람: eric00513
데이터를 추가한 사람: kth004, Lawali

알고리즘 분류

자료 구조
세그먼트 트리
분할 정복
스택

Solution

import java.io.*;
import java.util.Stack;
import java.util.StringTokenizer;

public class Main {
    public static int n;
    public static int[] histogram;
    public static long area;
    public static Stack<Integer> stk;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
        StringTokenizer st;

        // 테스트케이스가 종료될 때까지 반복
        while(true) {
            st = new StringTokenizer(br.readLine());

            n = Integer.parseInt(st.nextToken());

            // 0인 경우 테스트 종료이므로 break
            if(n == 0) break;
            // 0이 아닌 경우 테스트 진행, 히스토그램을 담을 배열 선언
            histogram = new int[n];

            for(int i = 0; i < n; i++) {
                histogram[i] = Integer.parseInt(st.nextToken());
            }
            
            // 최대 넓이 계산 시작
            bw.write(String.valueOf(getArea(histogram.length)) + "\n");
        }

        bw.flush();
        bw.close();
        br.close();

    }

    public static long getArea(int len) {
        stk = new Stack<Integer>();
        area = 0;

        for(int i = 0; i < len; i++) {
            // 스택의 최상단 원소를 idx로 갖는 직사각형의 높이보다 현재 직사각형의 높이가 낮으면,
            // 지금까지 스택에 쌓여있는 직사각형의 넓이를 순차적으로 구해나간다.
            while(!stk.isEmpty() && histogram[stk.peek()] >= histogram[i]) {
                int height = histogram[stk.pop()];
                // (중요) 너비를 구할 경우
                // 1) 스택 최상단 원소를 제거 하였는데도 스택에 원소가 남아있는 경우, 직사각형이 더 존재한다는 것이므로,
                //    현재 idx보다 1작은 idx가 출발점(i-1)이고, 다음 직사각형의 idx(stk.peek())가 종료지점이다.
                // 2) 스택 최상단 원소를 제거 하였는데, 스택에 원소가 남아있지 않는 경우, 현재 idx가 너비가 되므로,
                //    너비는 i이다.
                long width = stk.isEmpty() ? i : i-1-stk.peek();

                // 넓이 계산할 때마다 최대 넓이 갱신
                area = Math.max(area, height*width);
            }

            // while문 종료 시 스택에 담겨있는 원소들의 직사각형 높이는 i번째 직사각형 높이보다 작다는 것이므로,
            // i번째 idx를 스택에 담는다.
            stk.push(i);
        }

        // 직사각형의 개수만큼 반복문을 수행하고 난 후에도 스택에 원소가 남아있을 수 있으므로,
        // 똑같은 과정을 진행한다.
        while(!stk.isEmpty()) {
            int height = histogram[stk.pop()];
            long width = stk.isEmpty() ? len : len-1-stk.peek();

            area = Math.max(area, height*width);
        }

        return area;
    }
}

Feedback

1. 스택의 top에 담겨있는 idx의 직사각형 높이보다 현재 직사각형의 높이가 높은 경우 스택에 담는다.
2. 스택의 top에 담겨있는 idx의 직사각형 높이보다 현재 직사각형의 높이가 작거나 같은 경우 높이를 갱신한다. (즉, 현재 직사각형의 높이보다 크거나 같은 직사각형 원소는 모두 스택에서 제거한다.)
3. 직사각형의 넓이는 스택에서 원소가 제거될 때 계산한다.

최대 넓이가 되기 위해서는 높이가 높거나, 너비가 넓어야 한다. 따라서 스택에 높이가 높은 직사각형들을 계속해서 담아가다가, 높이가 낮은 직사각형이 등장했을때, 이전 막대들은 현재 위치에서 보았을때 높이 내림차순으로 정렬이 되어있기 때문에, 너비를 하나씩 늘려주면서 높이는 그 시점의 높이를 사용하여 넓이를 구해주고, 넓이를 구해줄 때마다 최대 넓이를 비교하여 갱신해나간다.

즉, 높이 기준 오름차순으로 직사각형들을 쭈욱 쌓아오다가, 높이가 낮은 직사각형이 등장했을때, 현재 높이보다 낮은 직사각형이 등장할 때까지 역순으로 진행하며 넓이를 구해가는 것이다.

아래 블로그에 아주 잘 정리가 되어있어서 참고하여 겨우 해결할 수 있었다.
https://st-lab.tistory.com/255