
(2583) 영역 구하기 (Java)
| 시간 제한 | 메모리 제한 | 제출 | 정답 | 맞힌 사람 | 정답 비율 |
|---|---|---|---|---|---|
| 1 초 | 128 MB | 37437 | 21237 | 16682 | 57.165% |
문제
눈금의 간격이 1인 M×N(M,N≤100)크기의 모눈종이가 있다. 이 모눈종이 위에 눈금에 맞추어 K개의 직사각형을 그릴 때, 이들 K개의 직사각형의 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어진다.
예를 들어 M=5, N=7 인 모눈종이 위에 <그림 1>과 같이 직사각형 3개를 그렸다면, 그 나머지 영역은 <그림 2>와 같이 3개의 분리된 영역으로 나누어지게 된다.
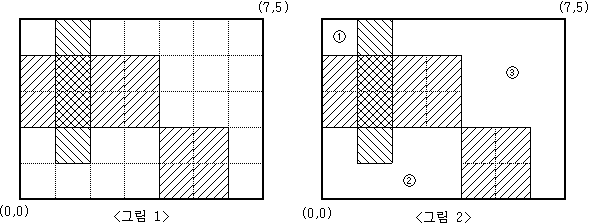
<그림 2>와 같이 분리된 세 영역의 넓이는 각각 1, 7, 13이 된다.
M, N과 K 그리고 K개의 직사각형의 좌표가 주어질 때, K개의 직사각형 내부를 제외한 나머지 부분이 몇 개의 분리된 영역으로 나누어지는지, 그리고 분리된 각 영역의 넓이가 얼마인지를 구하여 이를 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 M과 N, 그리고 K가 빈칸을 사이에 두고 차례로 주어진다. M, N, K는 모두 100 이하의 자연수이다. 둘째 줄부터 K개의 줄에는 한 줄에 하나씩 직사각형의 왼쪽 아래 꼭짓점의 x, y좌표값과 오른쪽 위 꼭짓점의 x, y좌표값이 빈칸을 사이에 두고 차례로 주어진다. 모눈종이의 왼쪽 아래 꼭짓점의 좌표는 (0,0)이고, 오른쪽 위 꼭짓점의 좌표는(N,M)이다. 입력되는 K개의 직사각형들이 모눈종이 전체를 채우는 경우는 없다.
출력
첫째 줄에 분리되어 나누어지는 영역의 개수를 출력한다. 둘째 줄에는 각 영역의 넓이를 오름차순으로 정렬하여 빈칸을 사이에 두고 출력한다.
예제 입력 1
5 7 3
0 2 4 4
1 1 2 5
4 0 6 2
예제 출력 1
3
1 7 13
출처
Olympiad > 한국정보올림피아드 > 한국정보올림피아드시․도지역본선 > 지역본선 2006 > 고등부 2번
문제의 오타를 찾은 사람: alphago92
데이터를 추가한 사람: hjhj97
잘못된 데이터를 찾은 사람: kookmin20103324
알고리즘 분류
그래프 이론
그래프 탐색
너비 우선 탐색
깊이 우선 탐색
Solution
import java.io.*;
import java.util.*;
public class Main {
public static int m, n, k;
public static int[][] paper;
public static boolean[][] visit;
public static class Pair {
int x, y;
Pair(int x, int y) {
this.x = x;
this.y = y;
}
}
public static Queue<Pair> q;
public static int[] dx = {1, 0, -1, 0};
public static int[] dy = {0, -1, 0, 1};
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(br.readLine());
m = Integer.parseInt(st.nextToken());
n = Integer.parseInt(st.nextToken());
k = Integer.parseInt(st.nextToken());
paper = new int[m][n];
visit = new boolean[m][n];
q = new LinkedList<Pair>();
for(int t = 0; t < k; t++) {
st = new StringTokenizer(br.readLine());
// 그림에서 주어진 x, y 축의 개념과 2차원 배열의 i, j의 개념이 다르기 때문에
// 생각을 잘해야한다. (여러번 찍어보면서 그리는 수밖에 없을듯)
int sX = Integer.parseInt(st.nextToken());
int eY = m - Integer.parseInt(st.nextToken());
int eX = Integer.parseInt(st.nextToken());
int sY = m - Integer.parseInt(st.nextToken());
for(int i = sY; i < eY; i++) {
for(int j = sX; j < eX; j++) {
paper[i][j] = 1;
}
}
}
br.close();
// 나머지 영역 찾기
List<Integer> list = findEtc();
bw.write(String.valueOf(list.remove(list.size()-1)) + "\n");
list.sort(Comparator.naturalOrder());
for(int temp : list) {
bw.write(String.valueOf(temp) + " ");
}
bw.flush();
bw.close();
}
public static List<Integer> findEtc() {
List<Integer> returnList = new ArrayList<Integer>();
int domain = 0; // 영역 개수
for(int i = 0; i < m; i++) {
for(int j = 0; j < n; j++) {
// 이미 방문한 칸이거나, 직사각형이 그려져 있다면 skip
if(visit[i][j] || paper[i][j] == 1) continue;
// 나머지 영역 시작점 세팅
q.offer(new Pair(i, j));
visit[i][j] = true;
domain++;
// 인접 칸 탐색
int area = 0; // 면적
while(!q.isEmpty()) {
area++;
Pair pollCell = q.poll();
for(int k = 0; k < 4; k++) {
int nx = pollCell.x + dx[k];
int ny = pollCell.y + dy[k];
// 종이의 범위를 벗어나거나, 직사각형이 그려져 있거나, 이미 방문했다면 skip
if(isNotRange(nx, ny) || paper[nx][ny] == 1 || visit[nx][ny]) continue;
// 인접칸을 큐에 세팅, 방문 처리
q.offer(new Pair(nx, ny));
visit[nx][ny] = true;
}
}
returnList.add(area);
}
}
returnList.add(domain);
return returnList;
}
public static boolean isNotRange(int x, int y) {
return (x < 0 || x >= m || y < 0 || y >= n) ? true : false;
}
}Feedback
그림에서 주어진 x, y 축의 개념과 2차원 배열의 i, j의 개념이 다르기 때문에 생각을 잘해서 그려야함
