[백준] 5525 IOIOI

🌭 문제 설명

• N+1개의 I와 N개의 O로 이루어져 있으면, I와 O이 교대로 나오는 문자열을 PN이라고 한다.

• P1 IOI

• P2 IOIOI

• P3 IOIOIOI

• PN IOIOI...OI (O가 N개)

• I와 O로만 이루어진 문자열 S와 정수 N이 주어졌을 때, S안에 PN이 몇 군데 포함되어 있는지 구하는 프로그램을 작성하시오.

---

🍗 제한 사항

---

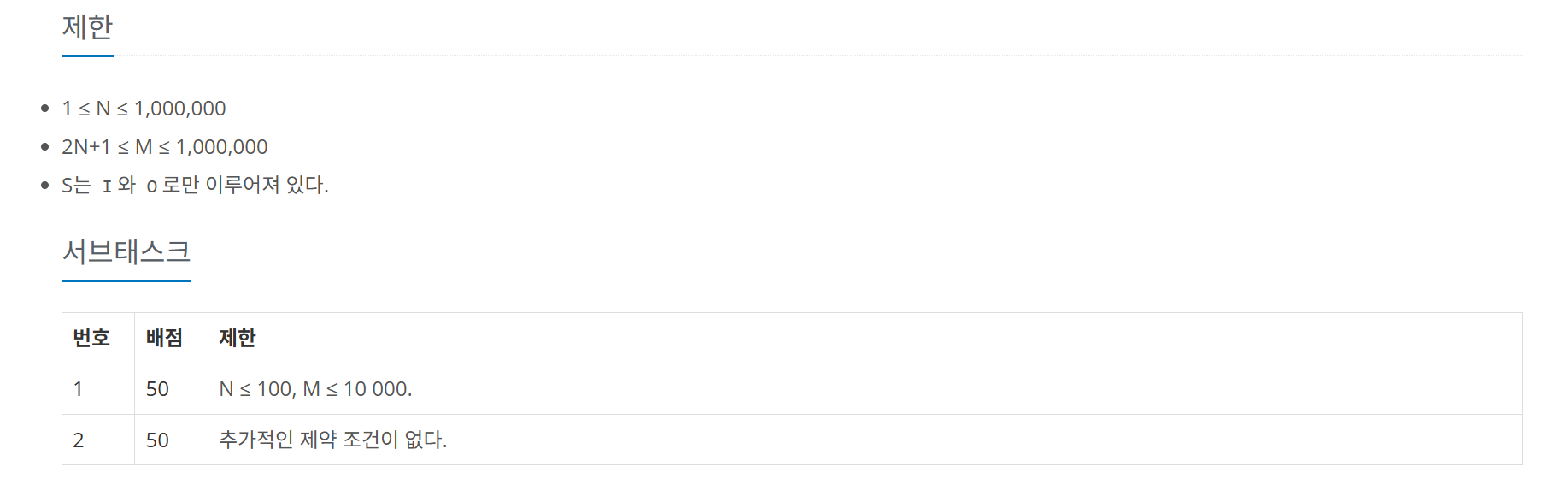
🎁 입출력 예시

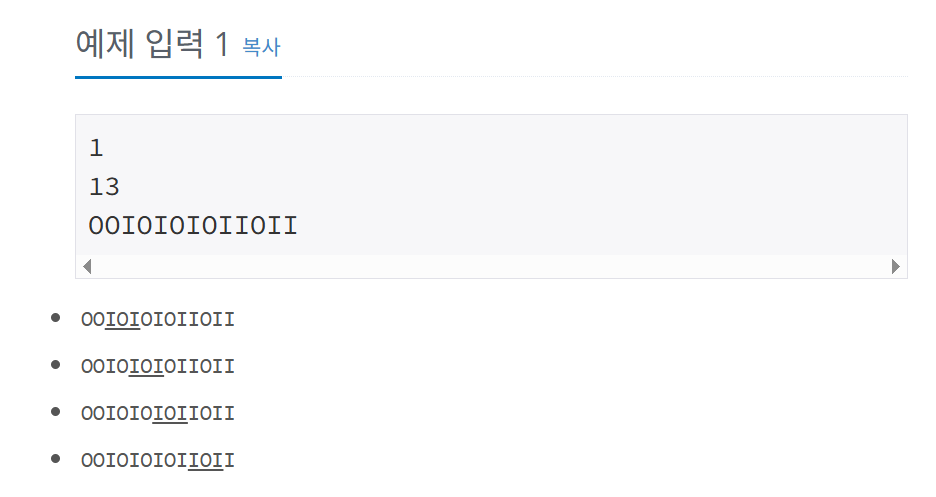
• 첫째 줄에 N이 주어진다. 둘째 줄에는 S의 길이 M이 주어지며, 셋째 줄에 S가 주어진다.

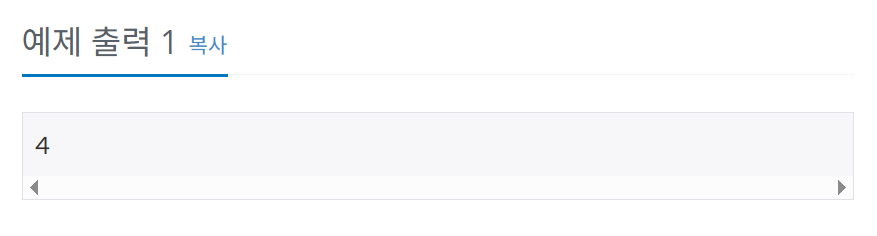
• S에 PN이 몇 군데 포함되어 있는지 출력한다.

---

😎 나의 풀이

N = int(input()) # 2
M = int(input()) # 13
S = input() # "OOIOIOIOIIOII"

cursor, count, result = 0, 0, 0

while cursor < (M - 1): # cursor가 M-1 보다 작을 동안 실행 (끝까지)
    if S[cursor:cursor + 3] == 'IOI': # 현재 위치부터 3글자를 잘라서 "IOI"인지 확인
        count += 1 # IOI면 count + 1
        cursor += 2 # cursor는 두칸 이동(I가 겹침)
        if count == N: # IOI가 N번 연속해서 나오면 result + 1
            result += 1
            count -= 1 # 다음 패턴을 위해 하나 줄인다.(다음 IOI 체크)
    else: # IOI가 아니면 cursor를 한 칸 이동한다.
        cursor += 1
        count = 0 # IOI 패턴이 끊기므로 count = 0 리셋

print(result)

1. 현재 위치를 의미하는 cursor, "IOI"가 몇번나왔는지 세는 count, 찾은 패턴의 개수를 나타내는 result를 초기화해준다.
2. 최소 3글자를 비교해야하므로 M - 1까지 반복
3. 현재 위치부터 3글자를 잘라서 "IOI"인지 확인한다.
4. IOI면 count에 1을 더해주고 cursor는 두칸을 이동한다.
5. count가 N번 연속해서 나오면 result에 1을 더해주고 다음 IOI를 체크하기 위해 count - 1을 한다.
6. IOI가 아니면 cursor를 한칸 이동하고, count는 IOI패턴이 끊기므로 0으로 리셋한다.
7. 누적된 result 출력

---

🧵 다른 풀이

N = int(input())
M = int(input())
S = input()

# 해쉬 값을 계산 하기 위한 준비물
mod = 1e9 + 7
po = [0] * M # 제곱한 값들 저장 배열
po[0] = 1 # 31^0 = 1 이기 때문에 1로 설정
for i in range(1, M):
  po[i] = po[i - 1] * 31 % mod # 이전 값에 31 곱하고 mod 나머지 연산
  
# Pn 만들기
Pn = "I"
for i in range(N):
  Pn += "OI"
  
# Pn의 해쉬값 계산
# 0에서 시작해서 매번 한자리씩 올림을 하고 현재 자릿수를 더해준다.
Pn_hash = 0
for i in range(len(Pn)):
  Pn_hash *= 31
  Pn_hash %= mod
  
  # A를 1로 했을 때 알파벳 값을 구하기 위해 ASCII 코드로 계산하면 I,O의 값을 알 수 있다.
  Pn_hash += ord(Pn[i]) - ord('A') + 1
  Pn_hash %= mod
  
  
# S[0:len(Pn)] S의 맨 처음 부분문자열은 무조건 계산해줘야 한다.(값을 다른데서 가져올 수 없음)
S_hash = 0
for i in range(len(Pn)):
  S_hash *= 31
  S_hash %= mod
  
  S_hash += ord(S[i]) - ord('A') + 1
  S_hash %= mod
  
# S의 부분 문자열들의 해쉬 값 계산
count = 0 # 답 출력 카운트
for i in range(0, M - len(Pn) + 1):
  if S_hash == Pn_hash:
    count += 1
  
  # S_hash 갱신
  # (OIOIO - 15*31^4)
  largest = ord(S[i]) - ord('A') + 1
  S_hash += mod - largest * po[len(Pn) - 1] % mod
  S_hash %= mod
  
  # 한자리수 올림
  S_hash *= 31
  S_hash %= mod
  
  # 새로 오는 알파벳 더해줌 
  # 맨 마지막은 새로 갱신할 필요없어서 맨 마지막 전까지 갱신 
  if i + len(Pn) < M:
    S_hash += ord(S[i + len(Pn)]) - ord('A') + 1
    S_hash %= mod
print(count)

1. 해쉬를 이용한 풀이이다.

---

• 해쉬 개념을 공부해서 풀이를 해보려고 했지만 막상 어려워서 풀이를 보고 코드만 이해했다. 😂