🌭 문제 설명
-
케빈 베이컨의 6단계 법칙에 의하면 지구에 있는 모든 사람들은 최대 6단계 이내에서 서로 아는 사람으로 연결될 수 있다. 케빈 베이컨 게임은 임의의 두 사람이 최소 몇 단계 만에 이어질 수 있는지 계산하는 게임이다.
-
예를 들면, 전혀 상관없을 것 같은 인하대학교의 이강호와 서강대학교의 민세희는 몇 단계만에 이어질 수 있을까?
-
천민호는 이강호와 같은 학교에 다니는 사이이다. 천민호와 최백준은 Baekjoon Online Judge를 통해 알게 되었다. 최백준과 김선영은 같이 Startlink를 창업했다. 김선영과 김도현은 같은 학교 동아리 소속이다. 김도현과 민세희는 같은 학교에 다니는 사이로 서로 알고 있다. 즉, 이강호-천민호-최백준-김선영-김도현-민세희 와 같이 5단계만 거치면 된다.
-
케빈 베이컨은 미국 헐리우드 영화배우들 끼리 케빈 베이컨 게임을 했을때 나오는 단계의 총 합이 가장 적은 사람이라고 한다.
-
오늘은 Baekjoon Online Judge의 유저 중에서 케빈 베이컨의 수가 가장 작은 사람을 찾으려고 한다. 케빈 베이컨 수는 모든 사람과 케빈 베이컨 게임을 했을 때, 나오는 단계의 합이다.
-
예를 들어, BOJ의 유저가 5명이고, 1과 3, 1과 4, 2와 3, 3과 4, 4와 5가 친구인 경우를 생각해보자.
-
1은 2까지 3을 통해 2단계 만에, 3까지 1단계, 4까지 1단계, 5까지 4를 통해서 2단계 만에 알 수 있다. 따라서, 케빈 베이컨의 수는 2+1+1+2 = 6이다.
-
2는 1까지 3을 통해서 2단계 만에, 3까지 1단계 만에, 4까지 3을 통해서 2단계 만에, 5까지 3과 4를 통해서 3단계 만에 알 수 있다. 따라서, 케빈 베이컨의 수는 2+1+2+3 = 8이다.
-
3은 1까지 1단계, 2까지 1단계, 4까지 1단계, 5까지 4를 통해 2단계 만에 알 수 있다. 따라서, 케빈 베이컨의 수는 1+1+1+2 = 5이다.
-
4는 1까지 1단계, 2까지 3을 통해 2단계, 3까지 1단계, 5까지 1단계 만에 알 수 있다. 4의 케빈 베이컨의 수는 1+2+1+1 = 5가 된다.
-
마지막으로 5는 1까지 4를 통해 2단계, 2까지 4와 3을 통해 3단계, 3까지 4를 통해 2단계, 4까지 1단계 만에 알 수 있다. 5의 케빈 베이컨의 수는 2+3+2+1 = 8이다.
-
5명의 유저 중에서 케빈 베이컨의 수가 가장 작은 사람은 3과 4이다.
-
BOJ 유저의 수와 친구 관계가 입력으로 주어졌을 때, 케빈 베이컨의 수가 가장 작은 사람을 구하는 프로그램을 작성하시오.
🍗 제한 사항

🎁 입출력 예시
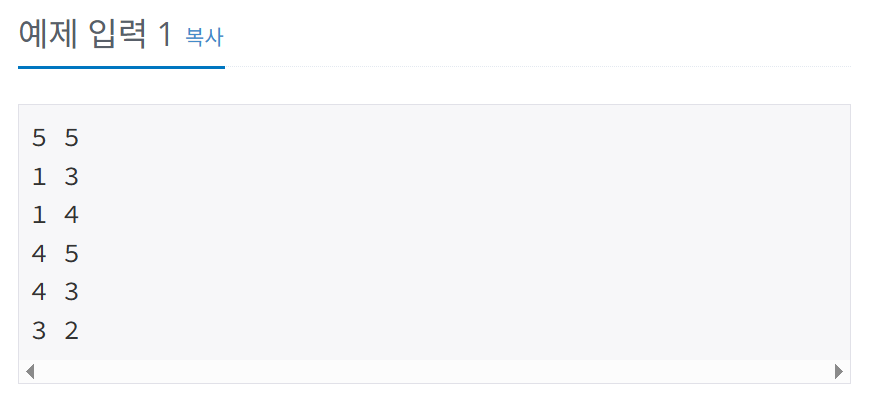
- 첫째 줄에 유저의 수
N(2 ≤ N ≤ 100)과 친구 관계의 수M(1 ≤ M ≤ 5,000)이 주어진다. 둘째 줄부터M개의 줄에는 친구 관계가 주어진다. 친구 관계는A와B로 이루어져 있으며,A와B가 친구라는 뜻이다.A와B가 친구이면,B와A도 친구이며,A와B가 같은 경우는 없다. 친구 관계는 중복되어 들어올 수도 있으며, 친구가 한 명도 없는 사람은 없다. 또, 모든 사람은 친구 관계로 연결되어져 있다. 사람의 번호는1부터 N까지이며, 두 사람이 같은 번호를 갖는 경우는 없다.
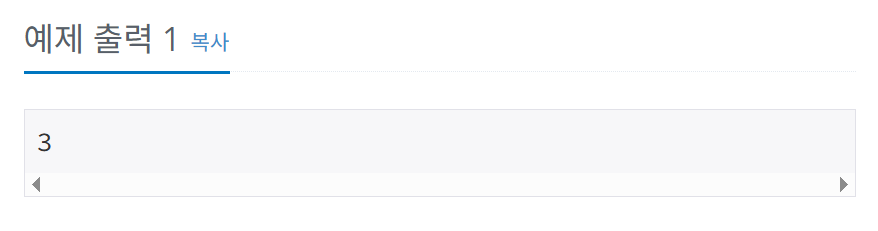
- 첫째 줄에 BOJ의 유저 중에서 케빈 베이컨의 수가 가장 작은 사람을 출력한다. 그런 사람이 여러 명일 경우에는 번호가 가장 작은 사람을 출력한다.
😎 나의 풀이
import sys
from collections import deque
input = sys.stdin.readline
N,M = list(map(int, input().split()))
graph = [[] for _ in range(N)]
for _ in range(M):
a, b = list(map(int, input().split()))
graph[a - 1].append(b - 1)
graph[b - 1].append(a - 1)
def BFS(graph, start):
# i를 시작점으로 하는 BFS 수행
# 각 노드까지의 최단거리 구해서 다 합한다.
visit = [False] * N
# 최단거리 담아둘 배열
dist = [-1] * N
# BFS 큐 생성
queue = deque([start])
# i가 큐에 있으므로 True (방문함)
visit[start] = True
# i번째 값에는 0으로 설정 (자기자신 거리)
dist[start] = 0
while queue:
u = queue.popleft() # 현재 노드 꺼내기
for v in graph[u]: # 연결노드 탐색
if not visit[v]: # 방문하지 않았으면
queue.append(v) # 큐에 추가
visit[v] = True # 방문 표시
dist[v] = dist[u] + 1 # 최단거리 업데이트 (v까지 가는 거리는 현재 u까지 온 거리 + 1)
return sum(dist) # 모든 거리의 합 리턴 (케빈베이컨 수)
# 케빈베이컨 수의 최솟값 저장 변수 (초기값: 무한대)
min_kevin_bacon = float('inf')
# 가장 작은 케빈베이컨 수를 가진 사람 (초기값 -1)
min_person = -1
for i in range(N):
kevin_bacon = BFS(graph,i) # i번째 사람 케빈베이컨 수 계산
# i번째 사람의 케빈베이컨 수를 계산한 시점에서
# 현재까지의 min_kevin_bacon 값보다 i번째 사람의 케빈베이컨 수가 더 작다면
if kevin_bacon < min_kevin_bacon:
min_kevin_bacon = kevin_bacon # i번째 사람의 케빈베이컨으로 최솟값 갱신
min_person = i # 가장 작은 케빈베이컨을 갖는 사람의 번호가 담긴다.
# 결과 출력 (1부터 시작하는 번호로 변환)
print(min_person + 1)- 이번 문제 풀이에선
BFS를 함수로 빼서 사용했다. N,M을 입력 받고 , 노드를 담아둘graph선언a,b로 각 노드들을graph에 추가한다. (양방향)BFS를 수행하는데 문제에서 요구하는 각 노드까지의 최단거리를 구해서 합하면 된다.- 방문 배열인
visit을False로 초기화 하고, 최단거리를 담아둘 배열인dist를-1로 초기화 한다. BFS를 위한 큐를 만들고, 현재 시점에서i가 큐에 있으므로True로visit값을 바꾸고, 자기자신의 거리는 0이므로dist의 값을 0으로 만든다.queue가 없어질 때까지 반복한다. 현재 노드를 꺼내서u에 저장- 연결된 노드를 탐색하고 방문하지 않았으면 큐에 추가하고 해당 노드를 방문했다는 의미로
visit값을True로 업데이트 , 최단거리인dist의 값을 +1 해서 업데이트 해준다. - 모든 거리의 합을 리턴해준다.
- 케빈베이컨 수를 계산해주면 된다.
🧵 다른 풀이
from collections import deque
N, M = map(int, input().split())
arr = [[] for _ in range(N+1)]
for i in range(M):
u, v = map(int, input().split())
arr[u].append(v)
arr[v].append(u)
def bfs(start):
visited = [-1] * (N + 1)
q = deque()
q.append(start)
visited[start] = 0
while q:
node = q.popleft()
for next_node in arr[node]:
if visited[next_node] == -1:
visited[next_node] = visited[node] + 1
q.append(next_node)
total = sum(visited)
return total
min_total = float("INF")
ans = 0
for i in range(1, N+1):
total = bfs(i)
if total < min_total:
min_total = total
ans = i
print(ans)BFS를 이용한 풀이이다.
BFS를 이용해서 최단거리까지 구하는 방법은 처음 알게되었다. 좀 더 많이 풀어봐야할 것 같다.
