상관관계를 찾아서
0
발표자료 및 소스코드: https://github.com/YunOh21/eda_project
2023년 9월 6일부터 12일까지 5일간의 개인 EDA 프로젝트를 회고할 겸, 상관계수와 p-value에 대해 정리해 보려고 합니다.
- EDA란?
- Exploratory Data Analysis 탐색적 데이터 분석
- 그래프 분석, 패턴 발견
- cf. CDA(Confirmatory Data Analysis) 확증적 분석
- 가설 검정
- Exploratory Data Analysis 탐색적 데이터 분석
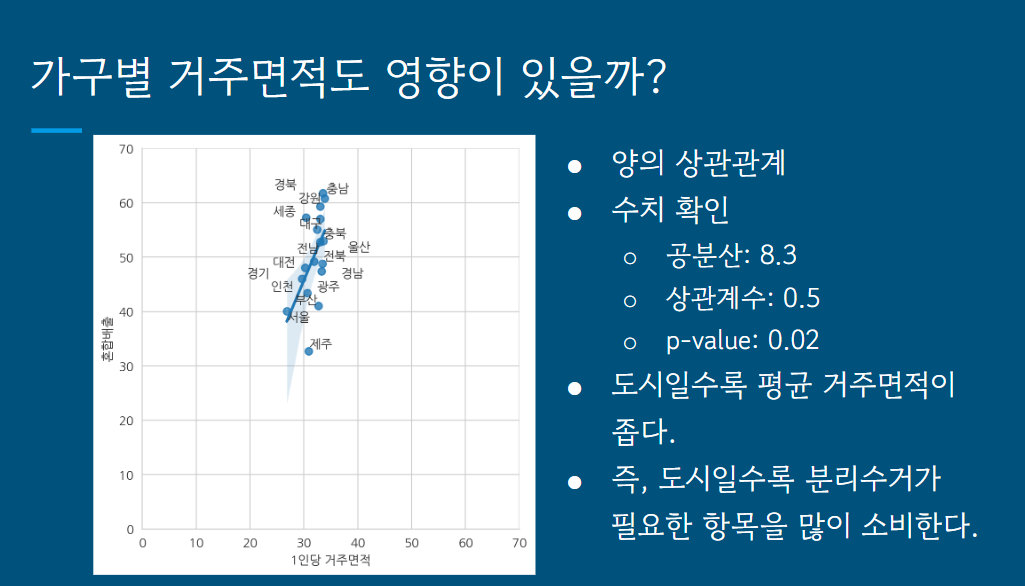
이번 프로젝트에서는 생활폐기물 배출 양상에 가구 특성이 영향이 있는지 확인해 보고자 했고, 상관관계를 알아내는 방법으로 공분산과 상관계수, p-value를 사용했습니다.
분산 variance
- 분산: 데이터의 분포 상태
- 데이터가 넓게 분포하면 분산 값이 크다
- 데이터가 촘촘하게 분포하면 분산 값이 작다
- 평균을 구한 다음, 각 값이 그 평균으로부터 얼마나 떨어져있는지(즉 그 편차)를 조사한다
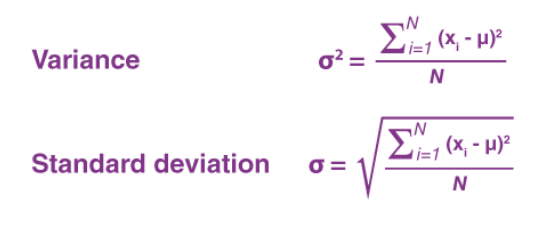
- 편차의 총합은 0이 되므로, 편차를 제곱해 그 제곱의 평균을 구한 값을 분산이라 한다.
- 편차 제곱의 총합 / 변량의 개수
- 이 값의 제곱근이 표준편차
공분산 covariance
- 공분산: 분산을 변수 2개에 확장한 개념
- x의 편차와 y의 편차를 곱한 값의 평균
- x의 변화량과 y의 변화량을 곱한 값
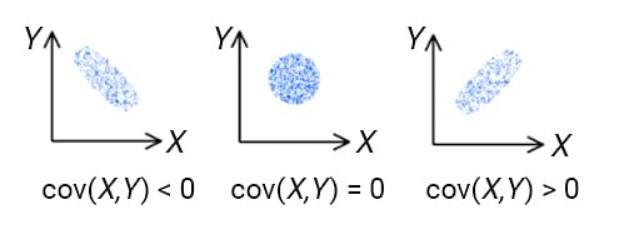
- 공분산은 변하는 방향을 나타낸다.
- x의 편차도 크고 y의 편차도 크면 공분산은 크다.
- 공분산이 크다는 것은 같은 방향으로 커진다는 것이다.
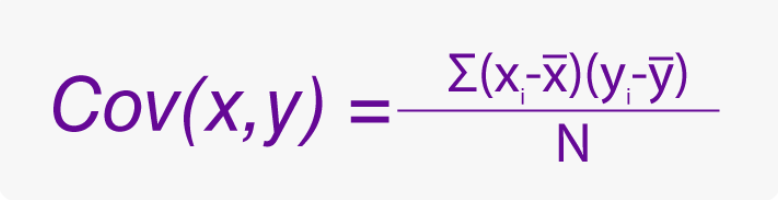
상관계수
- 가장 많이 사용되는 것은 피어슨 상관계수(Pearson Correlation Coefficient)
- 공분산을 표준편차의 곱으로 나눈 값
- cf. 결정계수, 스피어만 상관 계수
- 두 변량 x, y 사이의 상관관계의 정도를 나타내는 수치로, 알파벳 r로 표시한다
- r은 항상 -1과 1사이의 값
- 양의 상관관계가 있으면 r > 0
- 음의 상관관계가 있으면 r < 0
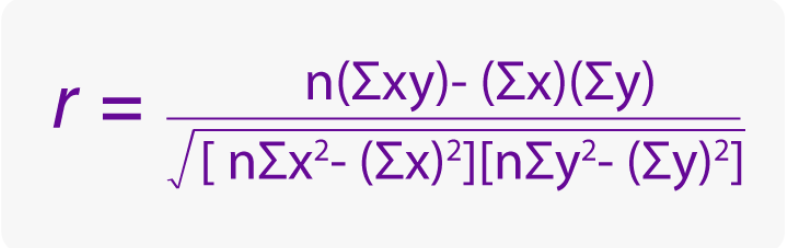
그런데 찾다 보니 p-value라는 것이 있다고 하는데...
p-value
- 어떤 가설이 우연히 일어났을 확률
- 귀무가설(null theory, 원하는 주장[대립가설]과 반대되는 가설) 하에서 극단적인 경우가 발생할 확률
- '신약의 치료효과가 좋다'가 대립가설이라면
- 단측검정에서 p-value: 신약의 치료효과가 없는 경우
- 양측검정에서 p-value: 신약의 치료효과가 없는 경우 + 신약으로 인해 병이 악화되는 경우 => 양측검정을 사용하는 것이 좋다
- p-value가 0.05 이하이면 신뢰할 만하다고 본다.
위 프로젝트에서는 p-value가 0.11인 상관계수도 89%면 신뢰할 만하다고 생각하면서 구해진 결과에 포함했습니다만... 진지한 통계라면 0.05를 넘어가는 값들은 버렸어야 했겠고 상관계수도 스피어만이나 결정계수도 사용해보고 p-value를 구하는 방법도 여러 가지 해 봤다면 더 좋았겠습니다.
scipy.stat.pearsonr
scipy.stats.pearsonr(x, y, *, alternative='two-sided', method=None)[source]params
- x: array-like
- y: array-like
- alternative: {‘two-sided’, ‘greater’, ‘less’}, optional
- 옵션 명시 없으면 two-sided가 기본값
- greater: 단측검정(양의 상관관계)
- less: 단측검정(음의 상관관계)
- method: ResamplingMethod, optional
- p-value의 계산방법 명시, 없으면 문서에 나온 대로 계산
- PermutationMethod, MonteCarloMethod 사용 가능
- Permutation Method: 순열 셔플링 -> 중요한 독립변수는 permutation함으로써 늘어난 오차가 클 것을 이용하여 어떤 변수가 중요한지 알아냄
- Monte Carlo Method: 반복된 무작취 추출을 이용하여 함수의 값을 수리적으로 근사하는 알고리즘 (엔리코 페르미가 중성자의 특성을 연구하기 위해 이 방법을 사용한 것으로 유명)
returns
- PearsonRResult
- statistic: float
- pearson product-moment correlation coefficient
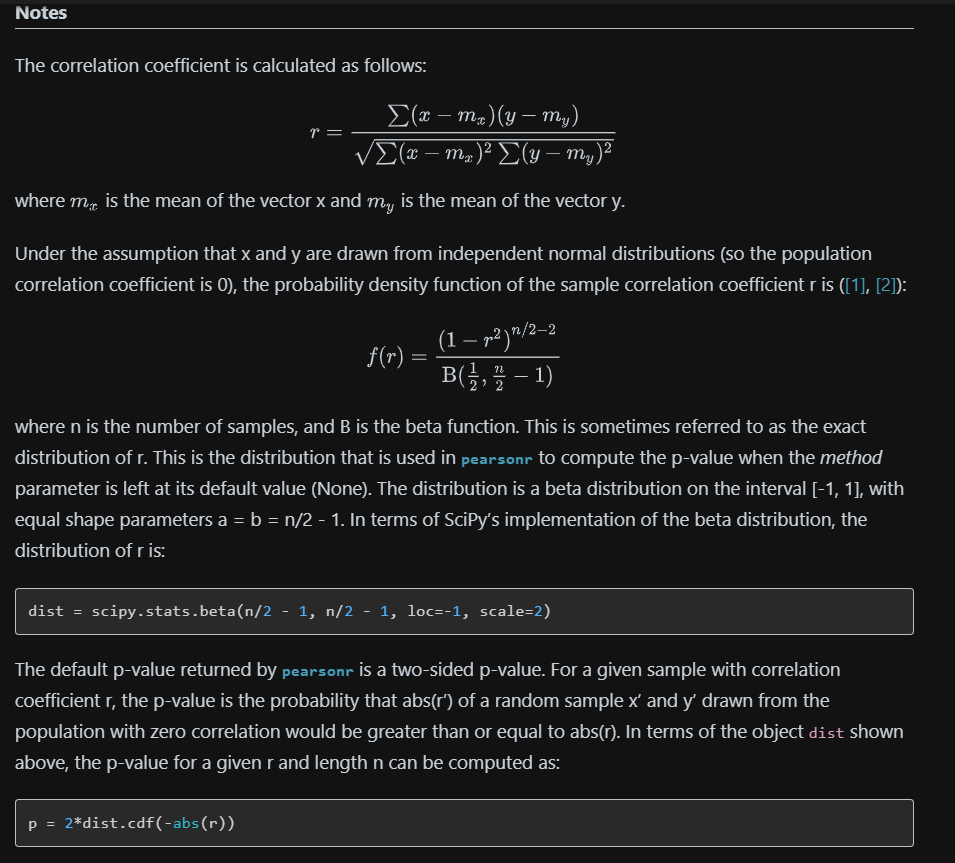
- pvalue: float
- p-value: 상관 관계가 0인 모집단에서 무작위로 추출한 표본 x'와 y'의 상관계수 r'의 절댓값이 상관계수 r의 절댓값보다 크거나 같을 확률
- p-value: 상관 관계가 0인 모집단에서 무작위로 추출한 표본 x'와 y'의 상관계수 r'의 절댓값이 상관계수 r의 절댓값보다 크거나 같을 확률
- statistic: float
선형의 관계가 없을 때 비선형 상관관계를 알아내는 방법으로 mutual information을 추천받았는데, 잘 이해하지 못한 상태로 활용하기 더 어려워서 다음에 다른 데이터 분석에 시도할 예정입니다.
- 참고자료
- https://terms.naver.com/entry.naver?docId=1063348&ref=y&cid=40942&categoryId=32215
- https://byjus.com/maths/variance-and-standard-deviation/
- https://byjus.com/covariance-formula/
- https://byjus.com/correlation-coefficient-formula/
- https://blog.naver.com/prayer2k/222624821291
- https://blog.naver.com/prayer2k/222626723108
- https://blog.naver.com/prayer2k/222787172572
- https://komok.tistory.com/40
- https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.pearsonr.html
- https://ko.wikipedia.org/wiki/%EB%AA%AC%ED%85%8C%EC%B9%B4%EB%A5%BC%EB%A1%9C_%EB%B0%A9%EB%B2%95
