Regression_Model
Remind for DeepLearning
파라미터 ( Parameter )
- a , b : 기울기 , y절편 → a: parameter → b: bias(편향)
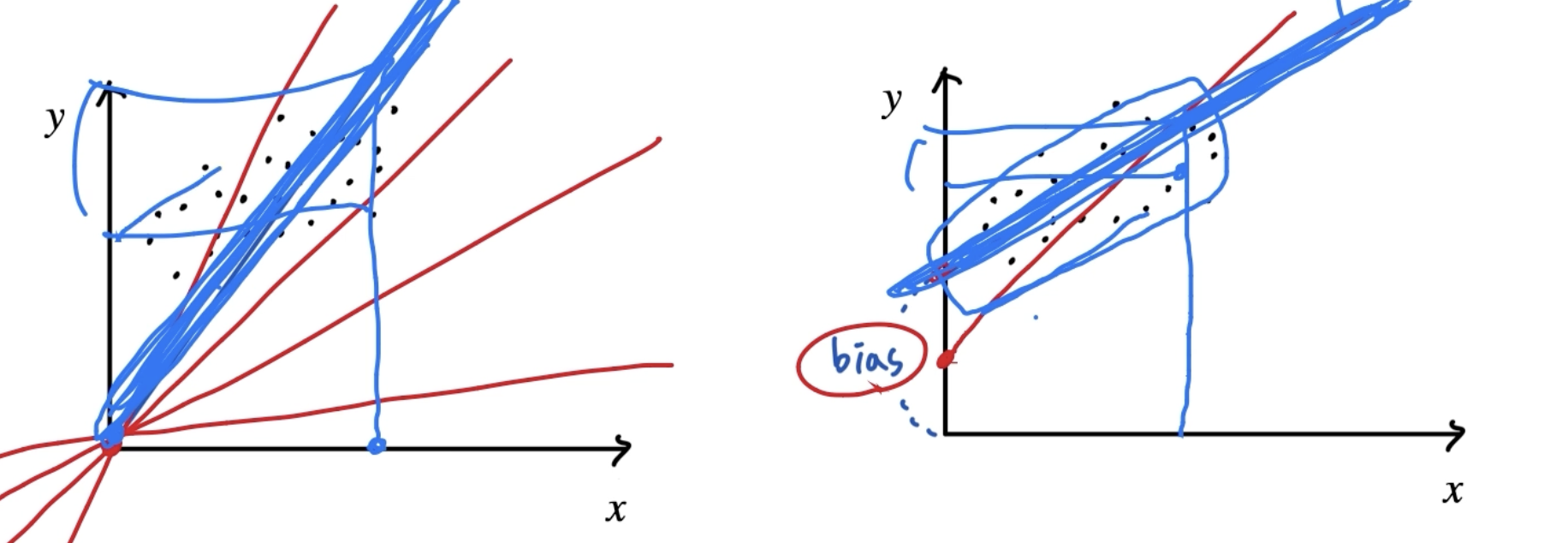
- 더 다양한 모델을- x : 데이터(feature,columns)
Model’s Capacity
- Capacity(복잡도)가 증가 할 수록 Overfitting 발생
Capacity 증가 → Overfitting 발생 → Generalization error 증가 → 새로운 Data에 사용하기 부적합
그럼 Overfitting을 어떻게 발견할 것인가?
- 그래프(test,train) 추이 확인
- 학습자가 논지를 전개하며 결과 값을 바라볼 때마다 상대적
새로운 Data에 대해서 좋은 결과를 도출 할 것인가?
-
Cross validation (교차 검증, aka 트테트테)
-
K-Fold
-
Regularization term (추후 DNN)
-
Drop - out & Batch Normalization (추후 DNN)
-
Training Data를 많이 확보하여 모델의 Feature를 늘리는 것
→ 이상적인 방법이지만 쉽지 않음
Linear Regession
- 종속변수(y)와 1개 이상의 독립변수(x) 사이의 선형 상관관계를 나타내는 회귀모델
- ⇒
- ⇒ 선형 결합
- a = : 기울기 = 가중치(중요도…etc)
- b: 절편(보정치) = bias(편향)
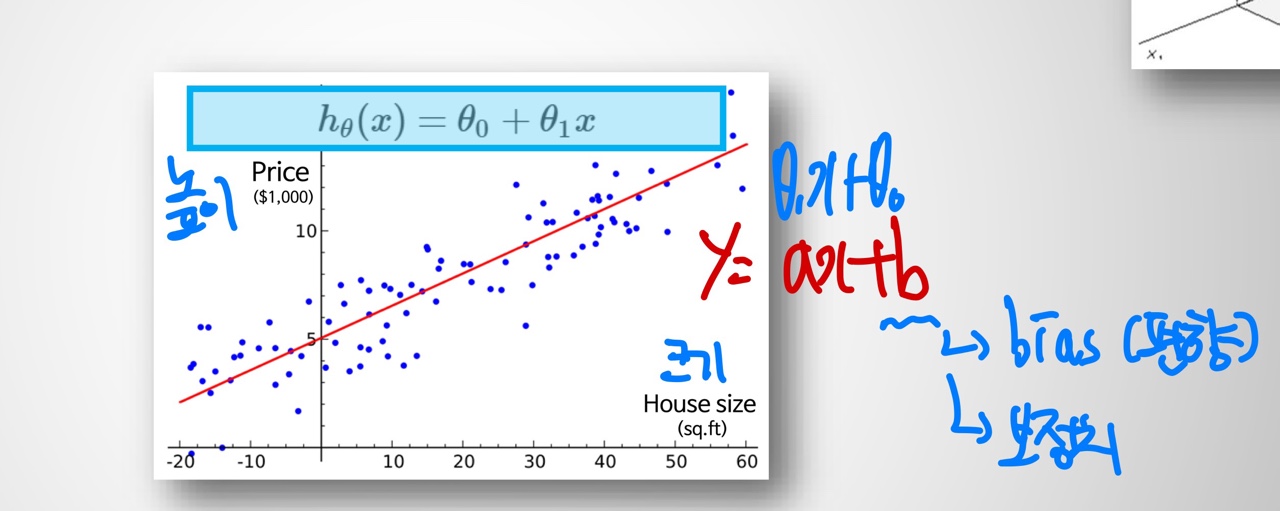
- 가장 적절한 들의 set을 찾는 것이 목표
- Cost Function : 예측 값과 실제 값의 차이를 기반으로 성능을 판단하기 위한 함수
- Linear의 경우 MSE가 최소가 되는 를 찾는다.
- 그럼 MSE 값이 최소가 되는 값을 어떻게 찾는가? → Gradient Descent Algortihm(경사하강법) 사용한다 가 변화하는 위치에서 미분한 값을 확인하여 기울기를 확인
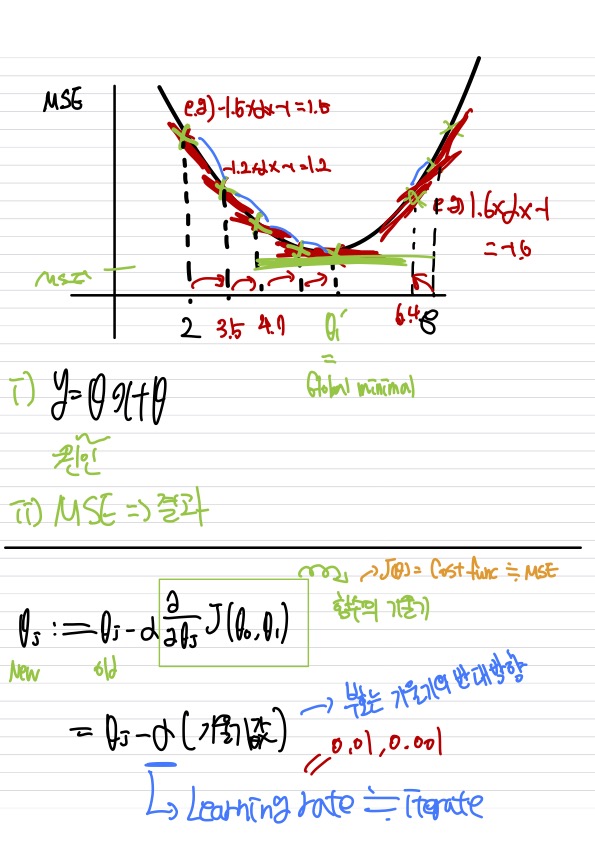
- 기울기가 음수일 때 : 오른쪽으로 이동 (+)
- 기울기가 양수일 때 : 왼쪽으로 이동 (-)
- 새로운 w = 기존 w + (기울기의 반대방향)
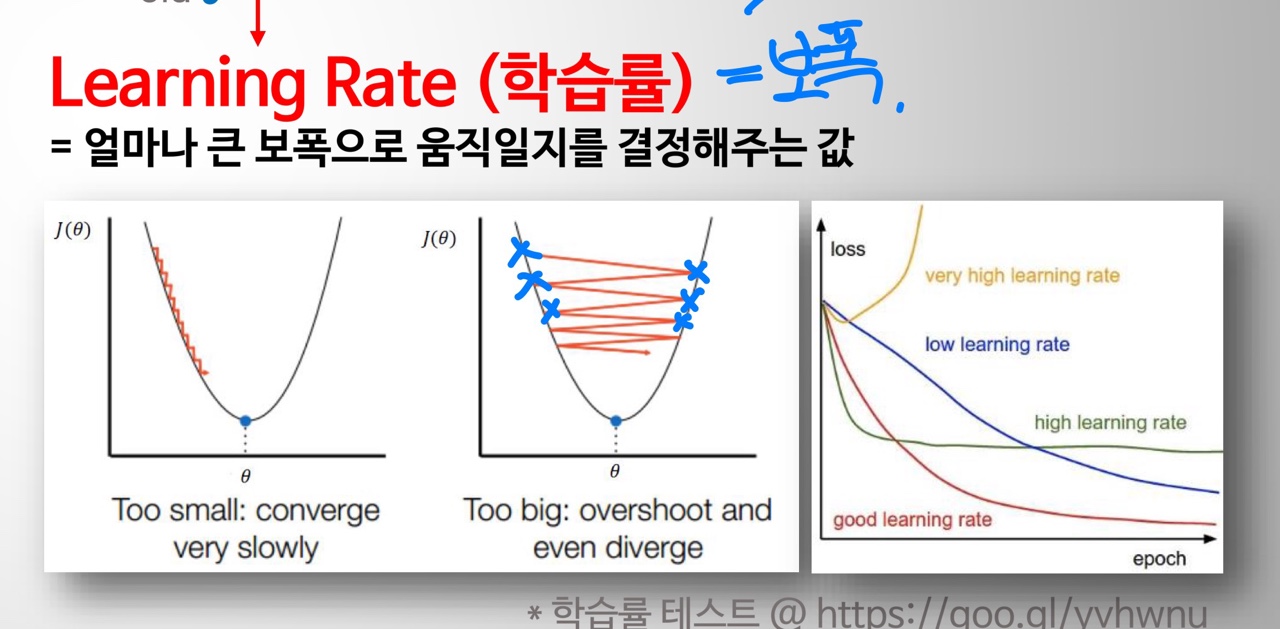
- = lr = Learning rate( 학습률 = 보폭) ⇒ Hyperparameter
- 값이 크면 좌우로 이동하면서 global minimum 값을 찾게 됀다.
- 값이 작을 경우 촘촘하게 global minimum 값을 찾게 됀다.