
👋 세 가지의 최단 경로 알고리즘을 통해 최단 경로를 마스터가 되어보자
✏️ 최단 경로 찾기
✔️ 최단 경로 알고리즘
지난 포스팅에서는 다이나믹 프로그래밍을 다루었는데, 이번 포스팅에서는 최단 경로 알고리즘을 파헤쳐보려 한다. 다이나믹 프로그래밍은 이름만 봐서는 어떤 건지 느낌이 전혀 안오는데 최단 경로는 이보다 더 직관적일 순 없다. 여러 갈래의 경로 중 가장 짧은 경로를 찾는 알고리즘을 말하는 것이다. EASY
오늘은 최단 경로 알고리즘의 종류 중 다익스트라, 플로이드 워셜, 벨만 포드 알고리즘 이렇게 총 3개를 살펴보겠다. 그럼 꼬꼬
✏️ 다익스트라 알고리즘 Dijkstra
최단 경로하면 가장 먼저 떠오르는 대표적인 알고리즘으로 다익스트라가 있다. (스펠링이슈로 맨날 다이그크스트라라고 함) 이 알고리즘은 그래프의 특정한 노드에서부터 다른 노드까지로 가는 각각의 최단 경로를 구한다.
알고리즘의 로직을 정리하면 아래와 같다.
✔️ 다익스트라 알고리즘 로직
시작 노드 설정 ▶️ 최단 거리 테이블 초기화 (무한대) ▶️ 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드 선택 ▶️ 해당 노드와 연결된 노드들의 최단 거리 갱신 ▶️ 반복
알고리즘의 원리에서 "방문하지 않은 노드 중 최단 거리가 가장 짧은 노드 선택" 이 부분에 주목해보자. 현재의 상황에서 가장 비용이 적은 노드를 선택한다는 동작은 그리디 알고리즘의 원리와 똑같다. 따라서 다익스트라 알고리즘은 그리디 알고리즘으로 분류될 수 있다!
다익스트라 알고리즘을 구현하는 방법에는 크게 두 가지 방법이 존재한다.
- 2차원 배열/벡터 사용 >> 구현은 쉽지만 시간, 메모리 초과 위험
- ⭐️ 우선순위 큐 사용 >> 구현은 어렵지만 PS에 굳
위의 두 가지 방법 중 잘 익혀야 하는 것은 당연하게도 우선순위 큐를 이용한 방법이다. 하지만 2차원 벡터를 이용하여 구현하는 방법 또한 알고 있어야 다익스트라 구현을 이해하는데 도움이 된다! 2차원 벡터를 이용한 구현 방법부터 알아보자.
백준 1753번의 조건을 따른 다익스트라 구현이다! 문제에 따라 조건이 다를 수 있으니 잘 확인하고 풀도록 하자. 해당 문제에서는 방향 그래프, 간선이 2개 이상일 수 있음 등등의 조건이 있다.
✔️ 다익스트라 구현 - 2차원 벡터 사용
#include <iostream>
#include <vector>
#include <algorithm>
#define INF 987654321
using namespace std;
//방문하지 않은 노드 중 현재의 최단 거리가 가장 짧은 노드의 번호 리턴
int smallest_node (int node, vector<int> &distance, vector<bool> &visited) {
unsigned long result = visited.size();
for (int i = 1; i < visited.size(); i++) {
if (visited[i] == false) result = distance[i] < result ? i : result;
}
return int(result);
}
void update_distance(int node, vector<vector<int>> &graph, vector<int> &distance, vector<bool> &visited) {
for (int i=1; i<distance.size(); i++) {
if (visited[i] == false && graph[node][i] != INF) {
distance[i] = distance[node] + graph[node][i] < distance[i] ? distance[node] + graph[node][i] : distance[i];
}
}
}
int main(int argc, const char * argv[]) {
int vertex, edge; //vertex, edge의 개수를 담는 변수
int start_node; //시작 node의 위치
std::cin >> vertex >> edge >> start_node;
std::vector<std::vector<int>> graph(vertex+1, std::vector<int>(vertex+1, INF));
std::vector<bool> visited(vertex+1, false); //각 노드에 대한 방문 여부
std::vector<int> distance(vertex+1, INF); //각 노드에 대한 현재의 최단거리
distance[start_node] = 0;
//graph의 노드들 간의 정보를 저장하는 2차원 vector
//(u, v, w): u -> v 로 가는 weight w의 edge가 존재
for (int i=0; i<edge; i++) {
int lnode, rnode, weight;
std::cin >> lnode >> rnode >> weight;
if (graph[lnode][rnode] != INF) graph[lnode][rnode] = graph[lnode][rnode] < weight ? graph[lnode][rnode] : weight;
else graph[lnode][rnode] = weight;
//graph[rnode][lnode] = weight; 단방향/양방향인지에 따라 설정 여부 다름
}
int temp = start_node;
visited[temp] = true;
while (true) {
update_distance(temp, graph, distance, visited);
temp = smallest_node(temp, distance, visited);
if (temp == vertex+1) break;
visited[temp] = true;
}
for (int i=1; i<distance.size(); i++) {
if (distance[i] == INF) std::cout << "INF" << "\n";
else std::cout << distance[i] << "\n";
}
return 0;
}
✔️ 다익스트라 구현 - 우선순위 큐
✏️ 벨만 포드 알고리즘 Bellman-Ford
벨만 포드 알고리즘은 시작 노드에서 다른 노드까지의 최단거리를 구하는 알고리즘이다. 앞에서 다룬 다익스트라와 비교를 하며 벨만 포드의 특징을 알아보자.
우선 두 알고리즘의 공통점은 시작 노드부터 다른 노드까지의 최단 거리를 구할 수 있다는 점이다. 그렇다면 차이점은 무엇일까?
다익스트라 Dijkstra
- 각 단계에서 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택하여 최단거리를 갱신
- 음의 가중치를 가지는 경우 최적의 해를 구할 수 없음
- 시간 복잡도가 빠름 O(ElogV) (E: # edges V: # vertexs)
벨만 포드 Bellman-Ford
- 각 단계에서 모든 edge를 전부 확인하면서 모든 노드 간의 최단 거리를 구함
- 음의 가중치가 있어도 최적의 해를 구할 수 있음
- 시간 복잡도가 느림 O(EV)
음의 가중치를 가진 간선이 있는 경우는 더 구체적으로 두 가지로 나눌 수 있다.
- 음수 간선 순환이 있는 경우
- 음수 간선 순환이 없는 경우
+) 음수 간선 순환
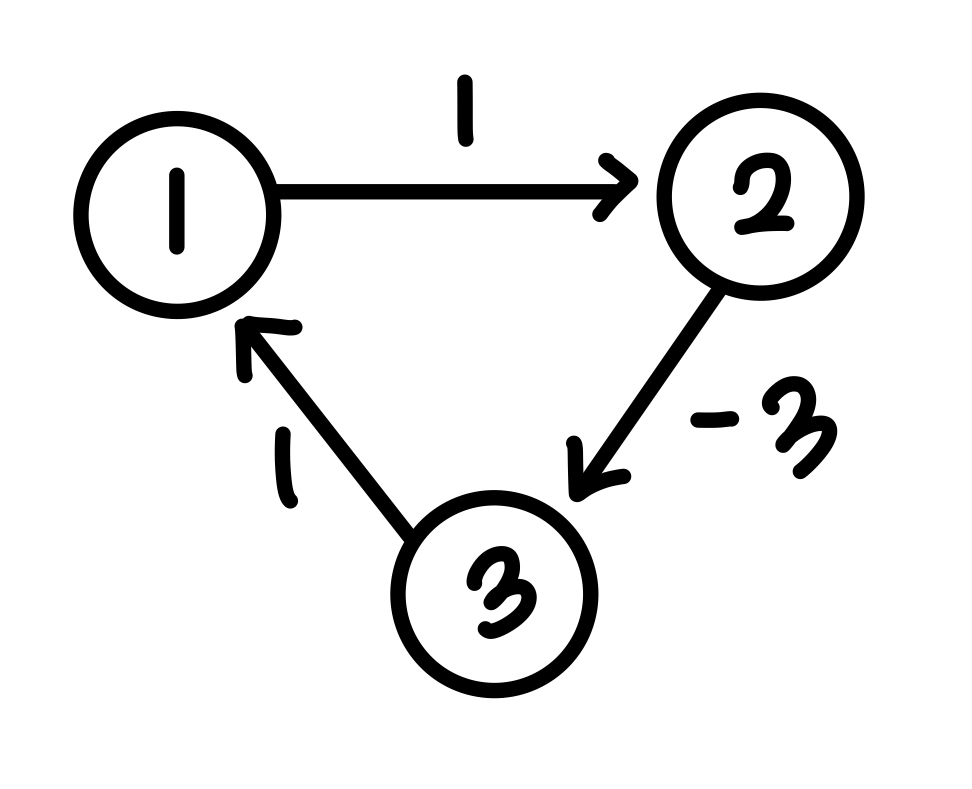
위 그림과 같은 그래프는 노드 1 시작해서 다시 노드 1로 돌아오는 경로가 존재한다. 즉 cycle 순환 경로가 존재한다. 이 순환 경로에 대한 가중치를 계산해보면 1 + (-3) + 1 = -1 음수값이 나오는데, 이 경우는 cycle을 계속해서 돌게 되면 가중치가 무한히 줄어들 수 있는 문제가 발생한다. 이렇게 cycle이 존재하고 그 cycle의 가중치의 합이 음수인 경우를 음수 간선 순환이라 부른다.
다익스트라와 벨만 포드의 가장 주된 차이점으로는 음의 가중치의 소화 여부인데 왜 다익스트라는 음의 가중치가 있는 경우 최적의 해를 구할 수 없고, 벨만 포드는 왜 구할 수 있는지 알아보자.
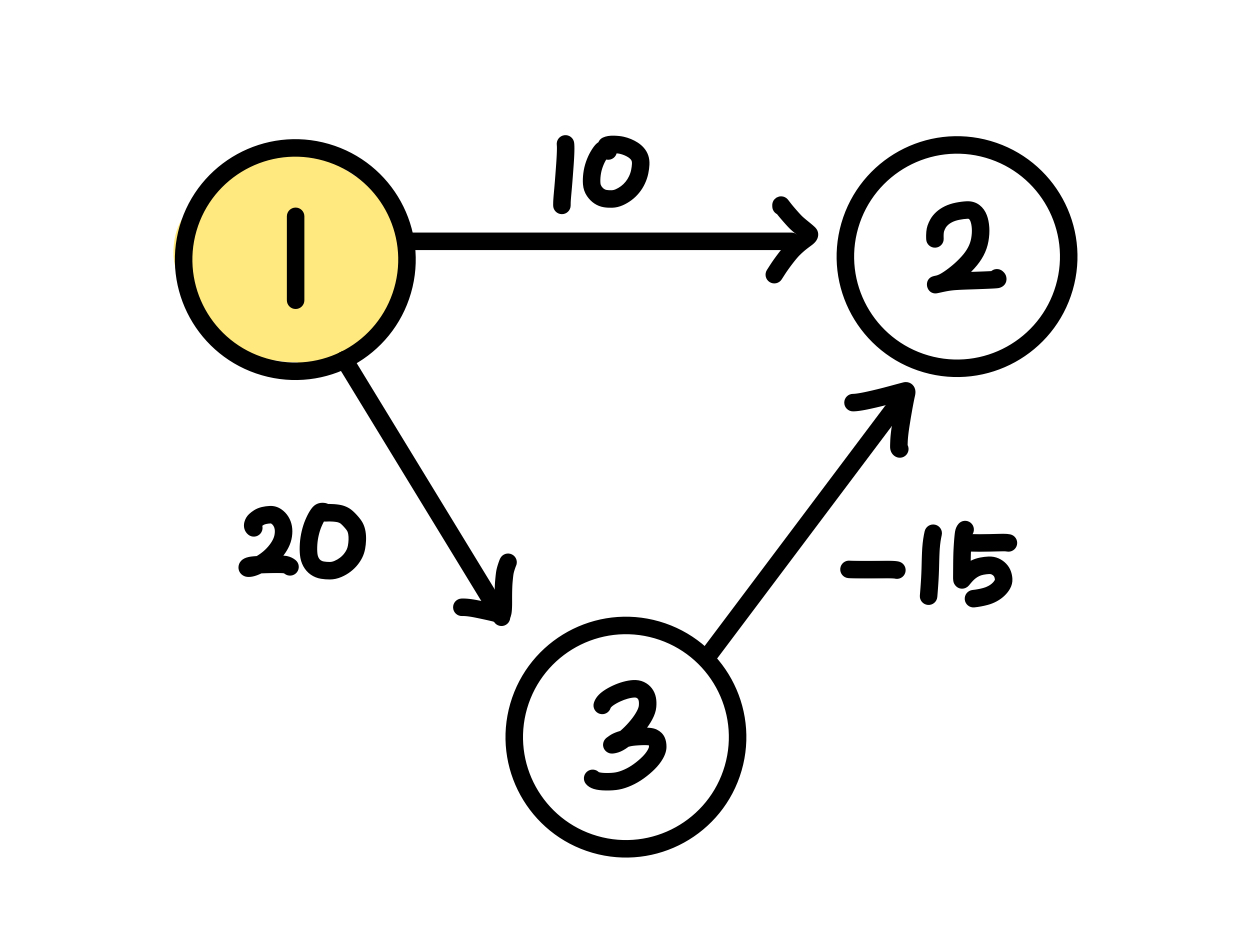
1에서 2로 가는 최단거리를 다익스트라를 이용하여 구해보자. 시작 노드 1과 연결된 노드 중 방문되지 않았고 최단거리가 가장 짧은 노드는 2이다. 따라서 1 → 2으로 가는 최단거리를 10 으로 구할 것이다. 그런데 사실 1 → 2의 최단거리는 1 → 3 → 2 경로로 가는 20 + (-15) = 5 이다.
이처럼 다익스트라는 현재의 상황에서 가장 최단경로가 짧은 것을 고르는 그리디 알고리즘의 일종이므로 음의 간선이 있는 경우는 최적의 해에 도달하지 못한다.
✔️ 벨만 포드 알고리즘 로직
시작 노드 설정 ▶️ 최단 거리 테이블 초기화 (무한대) ▶️ 연결된 모든 edge를 고려하여 최단 거리 테이블 갱신 ▶️ V-1번 반복
이 때 "최단 거리 테이블 초기화 (무한대) ▶️ 연결된 모든 edge를 고려하여 최단 거리 테이블 갱신" 이 부분을 한 번 더 반복했을 때 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재한다는 것을 확인할 수 있다.
벨만 포드의 구현을 통해 수행 과정을 더 자세히 알아보자.
✔️ 벨만 포드 구현
백준 11657번의 조건을 따른 벨만 포드 구현이다.
코드를 입력하세요