Unit1 회고

[자료구조/알고리즘]기초

🔆 자료구조

자료구조🗂

자료구조란 여러 데이터의 묶음을 체계적으로 정리하여 저장하고 활용하는 방법을 정의한 것을 의미하는데 한마디로 말하자면 데이터를 효율적으로 다루는 방법을 정의한 것이다.

• 데이터: 문자, 숫자, 소리, 그림, 영상 등 실생활을 구성하고 있는 모든 값

• 자료구조의 분류
  

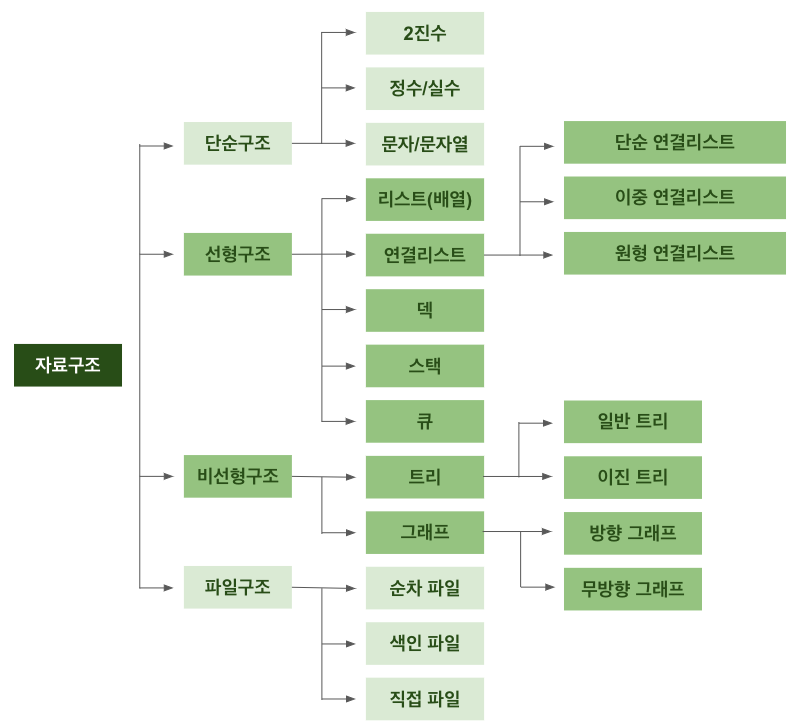
• 자료구조의 특징

  • 특정한 상황에 놓인 문제 해결에 용이
  • 다양한 자료구조를 알아두면 빠르고 정확한 문제 해결 가능

🔆 Stack과 Queue

Stack

Stack📚
: 데이터를 순서대로 쌓는 구조

Stack의 구조

• 끝이 막힌 골목길(Stack 자료구조)과 자동차(데이터)로 비유
• 입력과 출력이 한 방향으로 이루어지는 제한적 접근
• LIFO, FILO 구조
• Stack에 데이터를 넣는 것을 push, 데이터를 꺼내는 것을 pop이라고 함

Stack의 특징

1. LIFO(Last In First Out): 후입선출 구조
   • 데이터 저장 및 검색 프로세스가 빠름
   • 최상위 블록에서 데이터 저장 및 검색 가능
2. 데이터는 하나씩 넣고 꺼낼 수 있음
3. 하나의 입출력 방향
4. 저장되는 데이터는 유한하고 정적이어야 함
   • 스택에 저장되는 데이터는 일반적으로 로컬 변수, 포인터 및 함수 프레임
   • 함수 종료 시 최상위 블록이 지워지므로 해당 함수에 의해 스택에 들어간 모든 변수 삭제
   • 여기에 저장된 데이터가 정적 특성을 가져야만 컴파일 시간이 결정됨
5. 스택의 크기는 제한되어 있음

Stack의 사용 예제
<뒤로가기 앞으로가기>

1. 새로운 페이지로 접속 시 현재 페이지를 Prev Stack에 보관
2. 뒤로 가기 버튼을 클릭 시, 현재 페이지를 Next Stack에 보관하고 Prev Stack에 가장 나중에 보관된 페이지를 현재 페이지로 가져옴
3. 앞으로 가기 버튼을 클릭 시, Next Stack의 가장 마지막으로 보관된 페이지를 가져옴
4. 마지막으로 현재 페이지를 Prev Stack에 보관

Queue

Queue🚞
: 먼저 넣은 데이터가 먼저 나오는 자료구조

Queue의 구조

• 톨게이트(Queue 자료구조)와 자동차(데이터)로 비유
• FIFO, LILO 구조
• Queue에 데이터를 넣는 것을 enqueue, 데이터를 꺼내는 것을 dequeue라고 함
• 데이터가 입력된 순서대로 처리할 때 주로 사용

Queue의 특징

1. FIFO(First In First Out): 선입선출 구조
2. 데이터는 하나씩 넣고 꺼낼 수 있음
3. 두 개의 입출력 방향

Queue의 실사용 예제
<프린터로 문서 인쇄 작업 시>

1. 문서를 작성 후 출력 버튼 클릭 시 해당 문서는 인쇄 작업 (임시 기억 장치의) Queue에 들어감
2. 프린터는 인쇄 작업 Queue에 들어온 문서를 순서대로 인쇄

참고: Buffer🗄
여러 컴퓨터 장치들 사이에서 데이터를 주고 받을 경우 각 장치에 존재하는 속도나 시간 차이를 극복하기 위한 임시 기억 장치의 자료 구조로 Queue를 사용하며 이를 통틀어 Buffer라고 한다. 즉, Buffer란 불규칙적으로 발생한 이벤트를 규칙적으로 처리하기 위해 사용하는 영역이라고 할 수 있다.

🔆 Tree와 Graph

Tree

Tree🌲
: 그래프의 여러 구조 중 단방향 그래프의 한 구조로 계층적 자료구조

• 비선형 구조
• 사이클이 없는 하나의 연결 그래프

트리의 구조

• 노드(Node) : 트리 구조를 이루는 모든 개별 데이터
• 루트(Root) : 트리 구조의 시작점이 되는 노드
• 부모 노드(Parent node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 가까운 노드
• 자식 노드(Child node) : 두 노드가 상하관계로 연결되어 있을 때 상대적으로 루트에서 먼 노드
• 리프(Leaf) : 트리 구조의 끝 지점으로 자식 노드가 없는 노드

트리의 특징

• 깊이(Depth): 루트 노드(깊이:0)를 기준으로 하위 계층의 특정 노드까지의 깊이
• 레벨(Level): 같은 깊이를 가지고 있는 노드를 묶어 레벨로 표현하며 루트는 level1부터 시작하며 같은 레벨에 있는 노드는 형제 노드라 함
• 높이(Height): 리프 노트(높이:0)를 기준으로 루트까지의 높이
• 서브 트리(Sub tree): 큰 트리 내부에 트리 구조를 갖춘 작은 트리

트리의 실사용 예제
<컴퓨터 디렉터리 구조>
: 모든 폴더는 하나의 루트 폴더에서 시작되어 가지를 뻗어나가는 구조

Binary Search Tree

이진 트리(Binary Tree)🌿
: 자식 노드가 최대 두 개인 노드들로 구성된 트리

이진 트리의 종류

• 정 이진 트리(Full binary tree): 각 노드가 0개 혹은 2개의 자식 노드를 갖는 경우
• 포화 이진 트리(Perfect binary tree): 정 이진 트리이면서 완전 이진 트리인 경우
  • 모든 리프 노드 레벨 동일
  • 모든 레벨이 가득 채워짐
• 완전 이진 트리(Complete binary tree): 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하며 마지막 레벨의 왼쪽 노드는 반드시 채워져야 하는 경우

이진 탐색 트리(Binary Search Tree)🔎
: 이진 탐색(Binary search)과 연결 리스트(Linked list)를 결합한 이진 트리

이진 탐색 트리의 특징

• 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 구성
• 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 구성
• 좌우 서브 트리도 모두 이진 탐색 트리여야 함
• 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징

이진 탐색 트리의 탐색 과정
복잡도: O(최대 트리의 높이)

1. 루트 노드의 키와 찾고자 하는 값을 비교 후 찾고자 하는 값이라면 탐색을 종료
2. 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행
3. 찾고자 하는 값이 루트 노드의 키보다 크다면 오른쪽 서브 트리로 탐색을 진행
4. 트리 안에 찾고자 하는 값이 없더라도 최대 트리의 높이만큼 연산 및 탐색이 진행

Tree Traversal

트리순회🛸
: 특정 목적을 위해 트리의 모든 노드를 한 번씩 방문하는 것

트리 순회 방법

• 전위 순회: 부모 노드가 제일 먼저 방문되는 순회 방식
  • 부모 노드가 먼저 생성되어야 하는 트리를 복사할 때 사용
• 중위 순회: 부모 노드가 서브 트리의 방문 중간에 방문되는 순회 방식
  • 이진 탐색 트리의 오름차순으로 값을 가져올 때 쓰임
• 후위 순회: 루트를 가장 마지막에 순회하는 순회 방식
  • 트리를 삭제할 때 사용
• 레벨 순회: 루트 노드를 우선 탐색 후 다음 레벨의 노드를 탐색하는 순회 방식

Graph

Graph🌐
: 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조

그래프의 표현 방식

• 인접 행렬: 서로 다른 정점들이 인접한 상태인지 표시한 행렬로 2차원 배열의 형태로 표현
  • 인접 행렬 사용 상황
    • 두 정점 사이의 관계 유무 확인 시 용이
    • 가장 빠른 경로를 찾을 때 주로 사용
• 인접 리스트: 각 정점이 어떤 정점과 인접하는지를 리스트의 형태로 표현
  • 인접 리스트 사용 상황
    • 메모리를 효율적으로 사용하고 싶은 경우

그래프 관련 용어

• 정점 (vertex): 노드(node)라고도 하며 데이터가 저장되는 그래프의 기본 원소
• 간선 (edge): 정점 간의 관계를 나타내는 선
• 인접 정점 (adjacent vertex): 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점
• 가중치 그래프 (weighted Graph): 연결의 강도가 적혀져 있는 그래프를 뜻합니다.
• 비가중치 그래프 (unweighted Graph): 연결의 강도가 적혀져 있지 않는 그래프를 뜻합니다.
• 무(방)향 그래프 (undirected graph): 방향성이 존재하지 않는 양방향 그래프
• 진입차수 (in-degree) / 진출차수 (out-degree): 한 정점에 진입(들어오는 간선)하고 진출(나가는 간선)하는 간선의 개수
• 인접 (adjacency): 두 정점 간에 간선이 직접 이어져 있는 경우
• 자기 루프 (self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우
• 사이클 (cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있는 경우

BFS와 DFS

그래프의 탐색🔎
: 모든 정점들을 한 번씩 방문하는 것이 목적

그래프 탐색의 종류

• BFS(너비 우선 탐색)
  • 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 탐색 방법
  • 최단 경로 탐색 시 주로 사용
• DFS(깊이 우선 탐색)
  • 하나의 경로를 끝까지 탐색한 후, 찾는 값이 아니라면 다음 경로로 넘어가 탐색하는 탐색 방법
  • 한 정점에서 다음 경로로 넘어가기 전 해당 경로를 완벽하게 탐색할 때 사용

<오늘의 일기>
시간이 참 빠르게 지나 벌써 마지막 섹션에 들어섰다. 첫 유닛부터 자료구조와 알고리즘이라니.. 문제 풀다가 자괴감에 빠질 뻔 했는데 페어분께서 정신을 다잡아 주셔서 크게 좌절하지 않고 무사히 넘길 수 있었던 것 같다.
사실 이 분야에서 모든 게 처음인 나로서는 당연히 배울 것들이 많지만 특히 웹 개발에서는 아무리 잘하는 사람이더라도 공부에 끝이 없겠구나라는 생각을 많이 하게 된다.
그런 의미에서 더더욱 조급하게 생각하지 않고 내가 할 수 있는 선에서 적절한 속도로 최선을 다해야겠다.