지난 시간 복습

지난 6강에서는 TNN(Training Neural Network 첫번째 시간으로써 다양한 활성화 함수들을 배웠습니다. Sigmoid는 10여년 전에 신경망을 훈련할 때 꽤 인기가 있었던 활성화 함수로써 각광을 받았지만 입력값이 -∞ 또는 ∞로 갈수록 기울기 소실 문제가 발생한다는 점, zero-centered가 되지 않는다는 점, 지수함수적인 복잡한 계산 등의 문제로 인해 현재는 사용하지 않는 활성화 함수가 되었다는 점 다시 한번 살펴보게 되었습니다. tanh 함수도 마찬가지로 양 끝의 기울기 소실이 발생하죠. 이 두 가지 활성화 함수 대신에 이제 ReLU 함수를 기본적인 활성화 함수로써 선택을 하게 됩니다.

데이터 정규화에 대한 내용도 공부했었습니다. 데이터를 정규화해서 평균과 단위 분산이 0이 되도록 하는 방법에 대한 내용이었습니다.

그 중 zero-centered에 대한 내용을 첨언하였습니다. 이 빨간 점과 파란 점을 구분하는 선을 그리는 이진 분류에 대한 선형 그래프가 있습니다. 이 그래프를 통해 데이터 정규화를 왜 해야만 하는지를 다시 설명하고 있습니다.

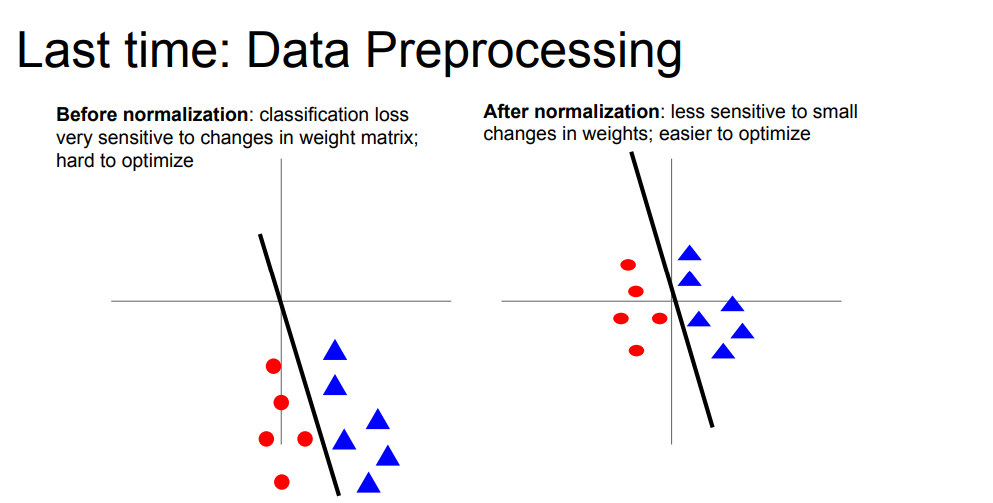
왼쪽 부분은은 데이터가 normalization이 안되어 있고, zero-centered가 되어 있지 않다는 것을 나타냅니다. 따라서 선이 조금만 틀어져도 분류를 잘못할 수 있습니다. w같은 파라미터의 조그만 변화에도 loss function이 굉장히 민감해질 수 있다는 뜻입니다.(robust하지 않다!!!)

반면 오른쪽의 경우는 파라미터의 변화에 덜 민감하다(robust하다!!!)고 할 수 있습니다. 즉, 오른쪽은 zero-centered가 되어 있기 때문에 optimization(최적화)이 가능하다는 것을 의미합니다.

이는 꼭 선형분류의 상황이 아니라 비선형 분류인 Neural Network에서도 적용이 됩니다. zero mean, zero - centered가 되어있지 않다면, 가중치 w 매트릭스의 작은 변화에도 해당 layer의 output에 큰 영향이 가해질 수 있는 것입니다.

Optimization

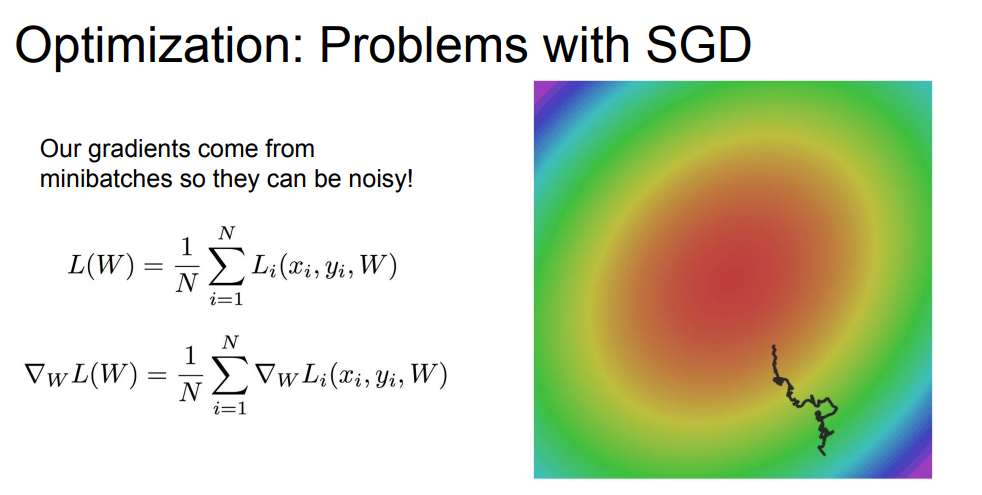
이 Optimization의 궁극적인 목표는 네트워크 가중치의 각 값에 대해 손실값이 얼마나 좋은지 나쁜지를 알려주는 손실 함수를 정의하는 것이라고 할 수 있습니다. 우측의 그림을 통해 optimization에 대해 이해해 볼 수 있습니다. 일단 우측의 그림은 x와 y 축이 가중치의 두 값으로 구성된 작은 2차원 문제에 대한 그림이며 w1, w2에 대해서만 최적화를 시키겠다는 뜻입니다. 플롯에 나와 있는 각기 다른 색상들은 손실값을 나타냅니다. 이 그래프에서 최소의 loss값을 갖는 w를 찾아서 빨간 지점에 도달하게끔 하는 것을 optimization을 시킨다고 설명하고 있습니다.

또한 왼편에 있는 식은 vanilla gradient descent를 하게 될 시 weights를 초기화를 해 주는 식이라고 합니다. 또한 batch 단위로 기울기가 음수이면 loss function의 최소점으로 이동함으로써 파라미터 업데이트를 반복하는 것을 SGD라고 합니다.
Gradient Descent 관련 참조 링크 : https://itrepo.tistory.com/23

SGD의 문제점

하지만 이 SGD는 문제점이 있습니다. 바로 taco shell problem이 있습니다. 현재 이 타원 궤도처럼 생긴 그림을 보면 빨간 점에서 최적점(이모티콘 모양이 있는 지점)으로 갈 때 x축 방향으로는 완만하고 y축 방향으로는 되게 크다(혹은 급하다라고 생각 가능)고 생각할 수 있습니다. 수평 방향인 x축 방향으로 이동하면 매우 느리고, 수직 방향인 y축 방향으로 가면 비교적 빠릅니다.

때문에 loss가 수직 방향으로만 sensitive해서 동일하게 이동하지 못하고, 위 그림과 같이 크게 방향이 튀면서 지그재그 형태로 이동하게 되는 현상이 발생합니다. 매우 느리고 불안정해 보입니다. high demension일수록 문제가 심각하다고 합니다. 위와 같이 지그재그 형태로 이동하게 되는 현상이 마치 taco의 shell처럼 보인다고 해서 taco shell problem이라고 합니다.

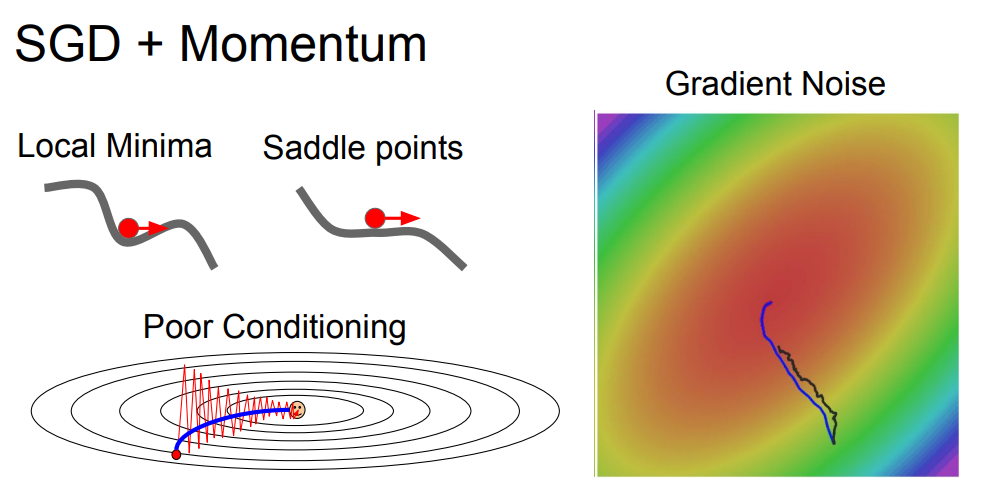
두 번째 문제점으로는 local minima와 saddle point에 빠지기 쉽다고 언급합니다. 위 슬라이드 중 위쪽 그래프가 local minima, 아래쪽 그래프가 saddle point를 나타냅니다.

local minima : 극댓값들 사이의 극솟값(기울기가 0이 되는 지점으로 빨간 점이 위치한 부분)에 안착하게 되는 경우를 말합니다. SGD 알고리즘은 기울기의 방향에 따라 이동하다가 기울기가 0인 점을 loss의 최솟값으로 찾는 알고리즘입니다. 이를 감안하고 위 그래프를 보게 되면 기울기가 0인 빨간 점의 위치를 찾았기 때문에 이 부분이 loss의 최솟값이구나라고 인지하게 되고 더 이상의 업데이트가 이루어지지 않게 됩니다.

saddle point : local minima와 마찬가지로 기울기가 0인 지점이 있는데 강의에서는 이 점을 안장점이라고 합니다(saddle point의 뜻). 이 saddle point는 골치 아픈 문제를 겪게 되는 부분이 있는데 바로 local minima에서보다 더 고차원일수록 잘 발생하고, 기울기가 0인 지점의 주변 부분의 기울기가 매우 작아져서 update가 굉장히 느려집니다.

세 번째 문제점은 SGD의 S에 해당하는 Stochastic이 문제를 일으킨다는 점입니다.
mini-batch를 쓰는 SGD 알고리즘은 배치마다 loss를 계산해서 전진해 나가는데, 이러한 방식이 expensive하다 혹은 비효율적이라고 합니다.
또한 미니배치마다 update를 위해 추정값을 이용하는데, 이것이 엄청나게 noise를 일으킵니다. 이 noise가 바로 위 그림에서 보이는 불규칙적인 형태의 선을 의미합니다. W를 쪼개서 추정값을 이용하는 방식이라 noise가 쌓이고 쌓여서 저런 선이 나타납니다.

해결책

SGD + Momentum

이 문제를 해결하기 위한 아이디어로 모멘텀(운동량)을 준다는 것을 내놓았습니다. 물리학적으로 가속도를 주는 개념입니다. 왼쪽은 SGD만 있는 식과 코드 구성이며 오른쪽이 SGD에 모멘텀을 부여한 식과 코드 구성입니다.

우측의 코드 구성 중 vx부분이 중요한데, 이는 기울기가 아닌 rho * vx로 step이 이루어져 있어서 기울기가 0인 지점에서도 가속도를 주며 update가 되도록 하는 알고리즘이기 때문입니다.
여기서 v는 가속도를 의미하며, rho는 보통 0.9, 0.99를 이용하여 가속도에 약간의 마찰값을 넣어주는 파라미터입니다.
매 step에서 old velocity에 friction으로 감소시키고, 현재의 gradient를 더해줍니다.

슬라이드의 공은 기울기가 0인 지점에서도 가속도로 step하기 때문에 update가 진행될 수 있습니다.

또한 taco shell 문제를 해결해 줄 수 있습니다. 기존 SGD는 빨간색 선처럼 지그재그 형태로 최적화 되었기 때문에 비효율적이고 느린 반면,
모멘텀 + SGD는 모멘텀이 수평방향으로 가속도록 유지하여 민감한 방향으로 총합을 줄여주어 noise들을 평균화시켜 줄 수 있습니다. 그리하여 파란색 곡선처럼 매끄럽게 최적화가 가능해 집니다.

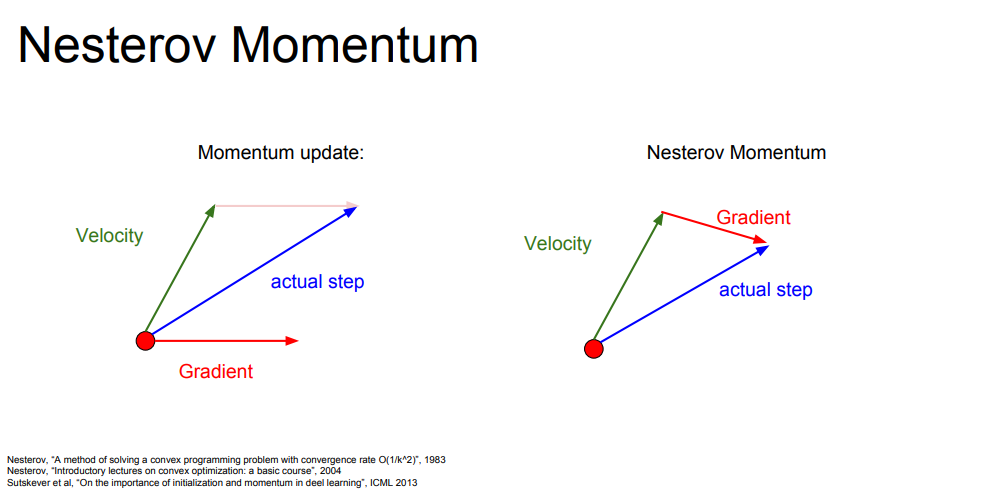
위 그림은 두 벡터의 방향이 average로 업데이트를 하는 모습을 나타내 주는 그림입니다. 이 중 왼쪽 그림에 좀 더 포커싱을 해서 보겠습니다. 빨간 점에서 velocity(속도) 뱡향으로 출발한 뒤, gradient를 계산합니다. 다시 원점으로 돌아와서 모멘텀 업데이트를 수행하고 actual step으로 최적화를 진행하는 내용입니다. 강의에서는 두 가지의 가중 평균에 따라 이동한다고 언급했습니다.
이 파란색 선, 즉 actual step으로 인해 gradient 추정값의 noise를 줄여줄 수 있습니다.
우측에는 Nesterov Momentum에 관련된 그림이 나오는데 우선 그림의 의미만을 놓고 볼 때는 velocity의 위치에서 방향을 예측한 후 gradient를 계산해서 actual step을 그리는 것이라는 것을 알 수 있습니다. 이를 error correction term이라고 합니다.

Nesterov Momentum

Nesterov Momentum에 대한 내용이 이어서 등장하는데, 이번에는 다소 복잡하게 보이는 식이 나와있습니다. 정리하자면 현재 v에서 step을 밟고 거기서 gradient를 계산하는 순서를 나타내는 것인데, 현재 지점에서 현재 velocity($v_{t+1}$)를 더하고 현재 v($v_{t+1}$)와 이전 v($v_{t}$)의 차이를 더해 줍니다. 코드로도 나와 있지만 코드보다는 옆의 식이 조금 더 이해하기 쉬울 수도 있습니다.

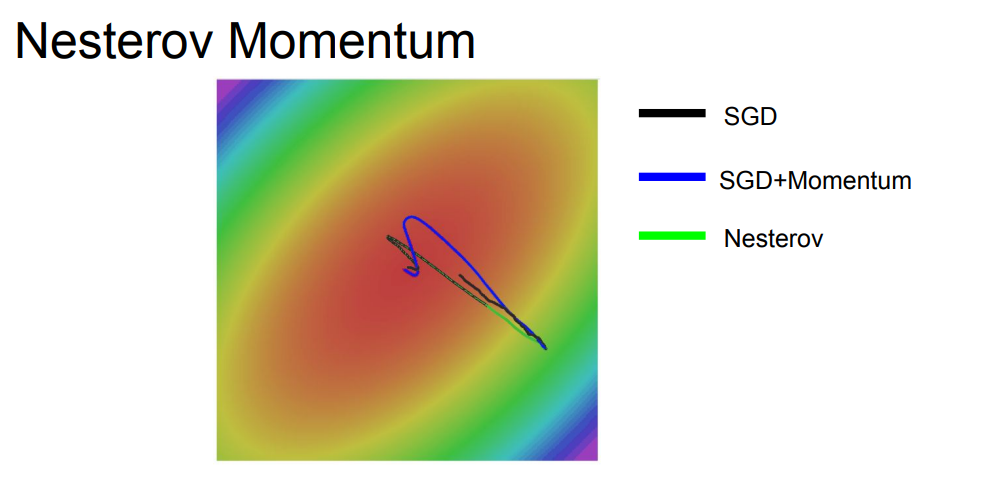
SGD는 느리고 모멘텀과 Nesterov는 약간 오버슈팅한 형태를 나타내는데, 이게 가속도가 있는 velocity 때문이라고 합니다.

모멘텀과 Nesterov(네스테로프)의 차이점은 네스테로프가 오버슈팅이 덜 일어난다는 점입니다.(위쪽 그림 참조)
현재 velocity와 old velocity 간의 차이를 더해준 error correction term 효과로 인한 것 같습니다.

수강생들이 질문한 내용들입니다.
Q1 : velocity의 initialization은 어떻게 시작되는가?
A1 : 이는 항상 0입니다. velocity는 하이퍼 파라미터가 아니기 때문입니다. 오히려 하이퍼 파라미터는 rho(마찰값)입니다.

Q2 : minima가 굉장히 sharp하고 narrow한 basin이라면 어떤가?(최종적인 최적점의 지점이 찾기 힘든 굉장히 좁은 지점이라면?)
A2 : 이 경우는 그리 좋지 않은 minima일 가능성이 높습니다. 이런 minima는 오버핏의 위험성이 큽니다. 데이터를 조금 더 수집한다면 사라질 것이며 flat한 minima로 수렴하길 원하는 이유는 더 더욱 강건하기때문입니다. SGD 모멘텀은 그런 sharp minima를 잘 스킵하기 때문에 오버핏의 위험성을 조금 줄일 수 있습니다.

이 외에도 우리가 생각해 볼 수 있는 방식으로는 AdaGrad, RMS Prop, 그리고 우리가 Optimization을 시키기 위한 코드를 작성할 때 무조건 한 번이상 봤었던 Adam에 대한 내용도 있습니다. 이에 관한 내용은 다음 시간에 ~~~

참조 링크 : https://inhovation97.tistory.com/24