알고리즘

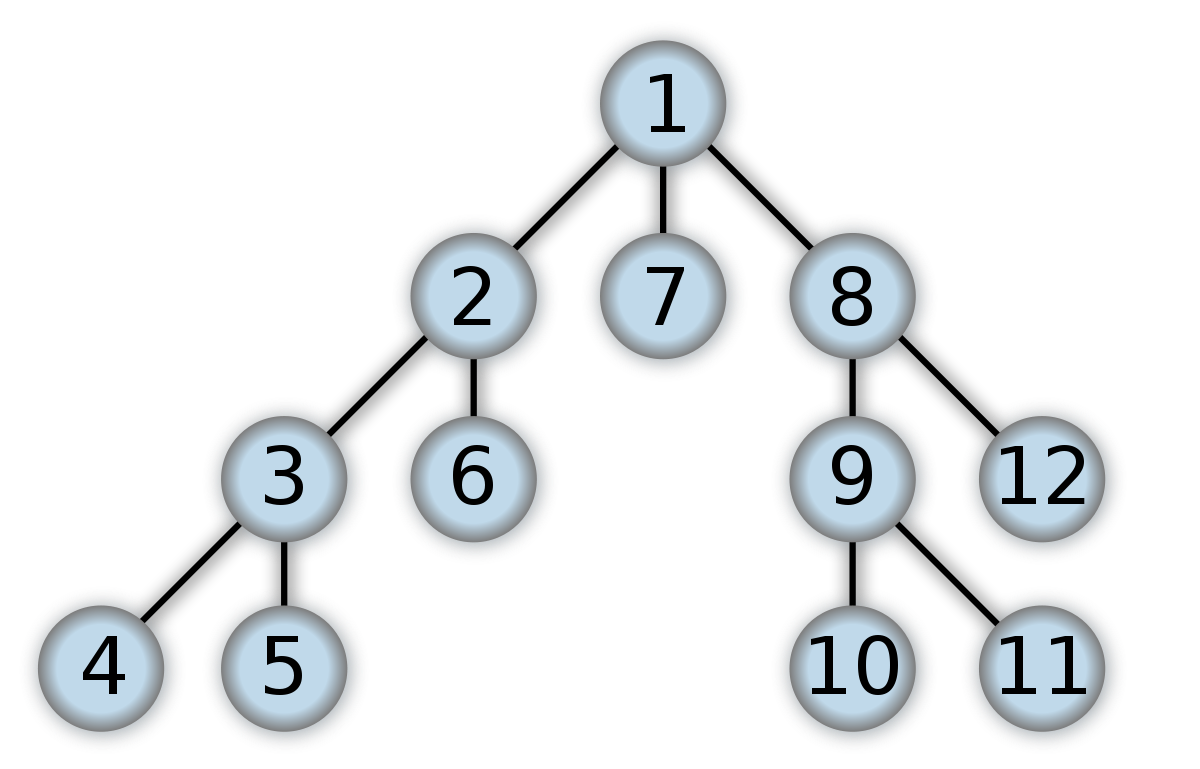
DFS 알고리즘을 어떻게 사용하는지와 언제 사용 가능한지를 정리하는 글이다. DFS > 재귀함수를 알고 있다는 가정으로 시작한다. > DFS는 깊이 우선 탐색이다. 밑에 그림을 보고 이해하는게 빠르다. 위와 같은 이진트리가 있다면 DFS는 깊이를 먼저 탐색하는

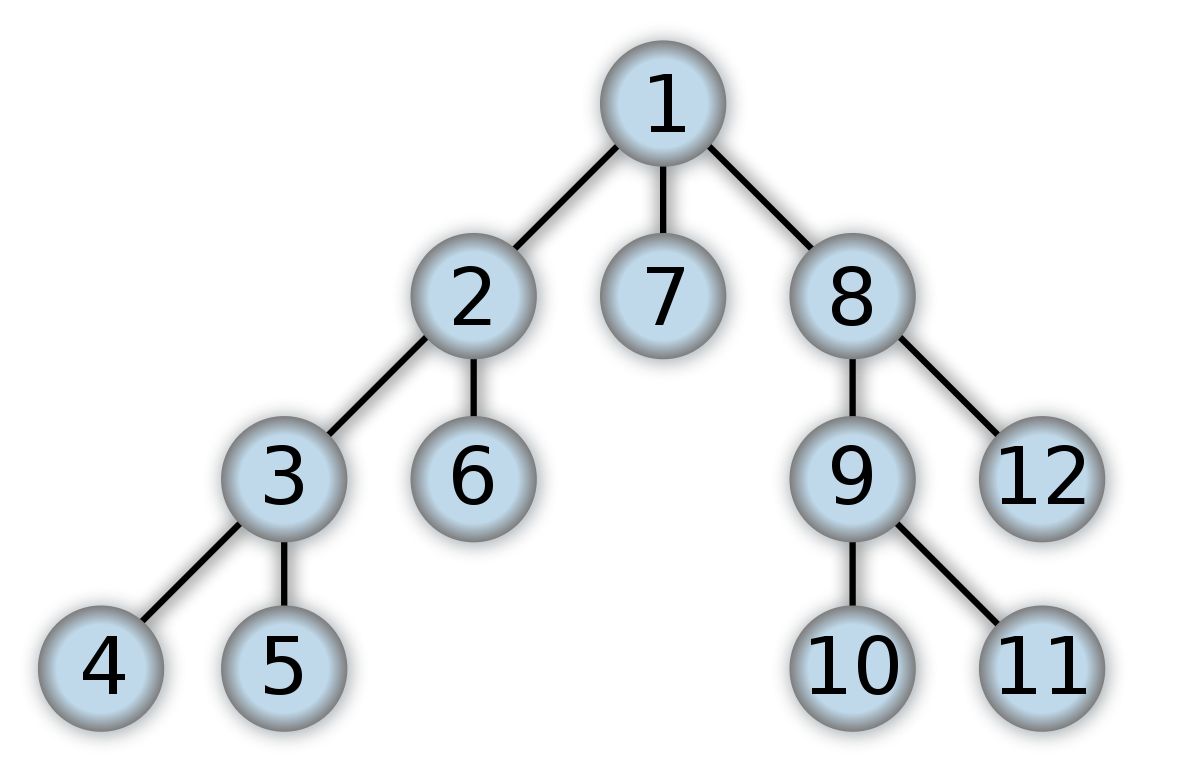
BFS 탐색이 무엇이고 어떤 문제에 활용할 수 있을지를 정리한 글이다. 개념 위 트리를 보고 너비 우선탐색으로 탐색을 하면 1 > 2 > 3 > 4 > 5 > 6 > 7로 탐색을 하는 방법이다. > 보통 BFS는 탐색을 할 때 최단거리를 찾을 때 주로 사용한다고

단순히 DFS와 BFS의 개념을 알고 있는지와 입력 받은 여러줄의 문자열을 잘 가공해서 사용할 수 있는지를 물어보는 문제라고 느껴졌다.입력 받은 노드간의 연결을 이중 배열에 넣어서 배열의 인덱스마다 양방향 노드의 도착 노드의 값을 넣어서 자료에 접근할 수 있도록 만들었

전형적인 미로 찾기 문제이다. 최단 거리를 구하는 문제이기 때문에 DFS와 BFS로 모두 푸는게 가능하다.하지만 DFS 같은 경우는 모든 경우의 수를 모두 탐색해서 그 중에 최소값을 찾는 방법이라 시간 복잡도가 BFS에 비해서 오래 걸리기 때문에 최단 거리를 구할 때는

그래프의 모든 경우의 수를 탐색하면 되는 문제 이기 때문에 DFS로 풀었다.근데 잘 풀고 나서 모든 반례를 대입해도 값은 나오는데 문제가 틀렸다고 나왔다. 그 원인은 각 노드별로 시작을 인덱스로 놓고 도착점을 값으로 넣기만 했는데 자세히 보니 양방향 노드이기 때문에 끝

그래프를 탐색해서 구하는 전형적인 DFS, BFS 문제이다.최단 거리를 구하는거가 아니고 모든 경우의 수를 탐색해서 구하는 문제 이기 때문에 DFS를 사용해서 문제를 풀었다.이차원 배열을 (0,0) 부터 (n-1,n-1) 지점까지 모두 돌면서 각 지점이 1인지를 판단하