BFS 탐색이 무엇이고 어떤 문제에 활용할 수 있을지를 정리한 글이다.

개념

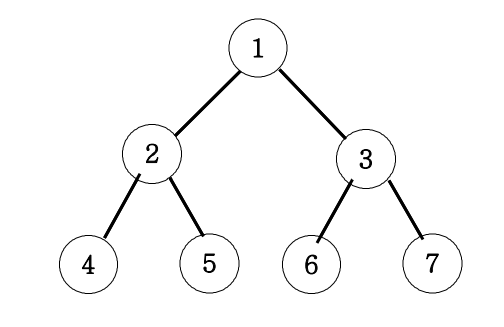
위 트리를 보고 너비 우선탐색으로 탐색을 하면 1 > 2 > 3 > 4 > 5 > 6 > 7로 탐색을 하는 방법이다.

보통 BFS는 탐색을 할 때 최단거리를 찾을 때 주로 사용한다고 보면 된다.

function solution() {
  let answer = "";
  let queue = [];
  queue.push(1);
  while (queue.length) {
    let v = queue.shift();
    answer += v + " ";
    for (let nv of [v * 2, v * 2 + 1]) {
      if (nv > 7) continue;
      queue.push(nv);
    }
  }
  return answer;
}

코드를 보면 queue 자료형을 사용하고 처음엔 출발 지점을 queue에 넣어 출발점에서 갈 수 있는 모든 지점을 queue 자료형에 순서대로 push 해주는 식으로 작성을 한다. 그러면 level 별로 level 2에서 조건에 충족하면 최단거리는 level 2로 답을 내도록 설계하기 때문에 최단 거리의 문제를 풀 때 BFS 문제를 사용하면 편리한걸 이 특징으로 파악할 수 있다.

예제

예제1)

현수는 송아지를 잃어버렸다. 다행히 송아지에는 위치추적기가 달려 있다. 현수의 위치와 송아
지의 위치가 수직선상의 좌표 점으로 주어지면 현수는 현재 위치에서 송아지의 위치까지 다음
과 같은 방법으로 이동한다. 송아지는 움직이지 않고 제자리에 있다.
현수는 스카이 콩콩을 타고 가는데 한 번의 점프로 앞으로 1, 뒤로 1, 앞으로 5를 이동할 수
있다. 최소 몇 번의 점프로 현수가 송아지의 위치까지 갈 수 있는지 구하는 프로그램을 작성
하세요.

이 문제는 현재 위치에서 송가지 위치까지를 이동하는 최단거리를 구하는 문제이기 때문에 BFS로 구하면 쉽게 구할 수 있다.

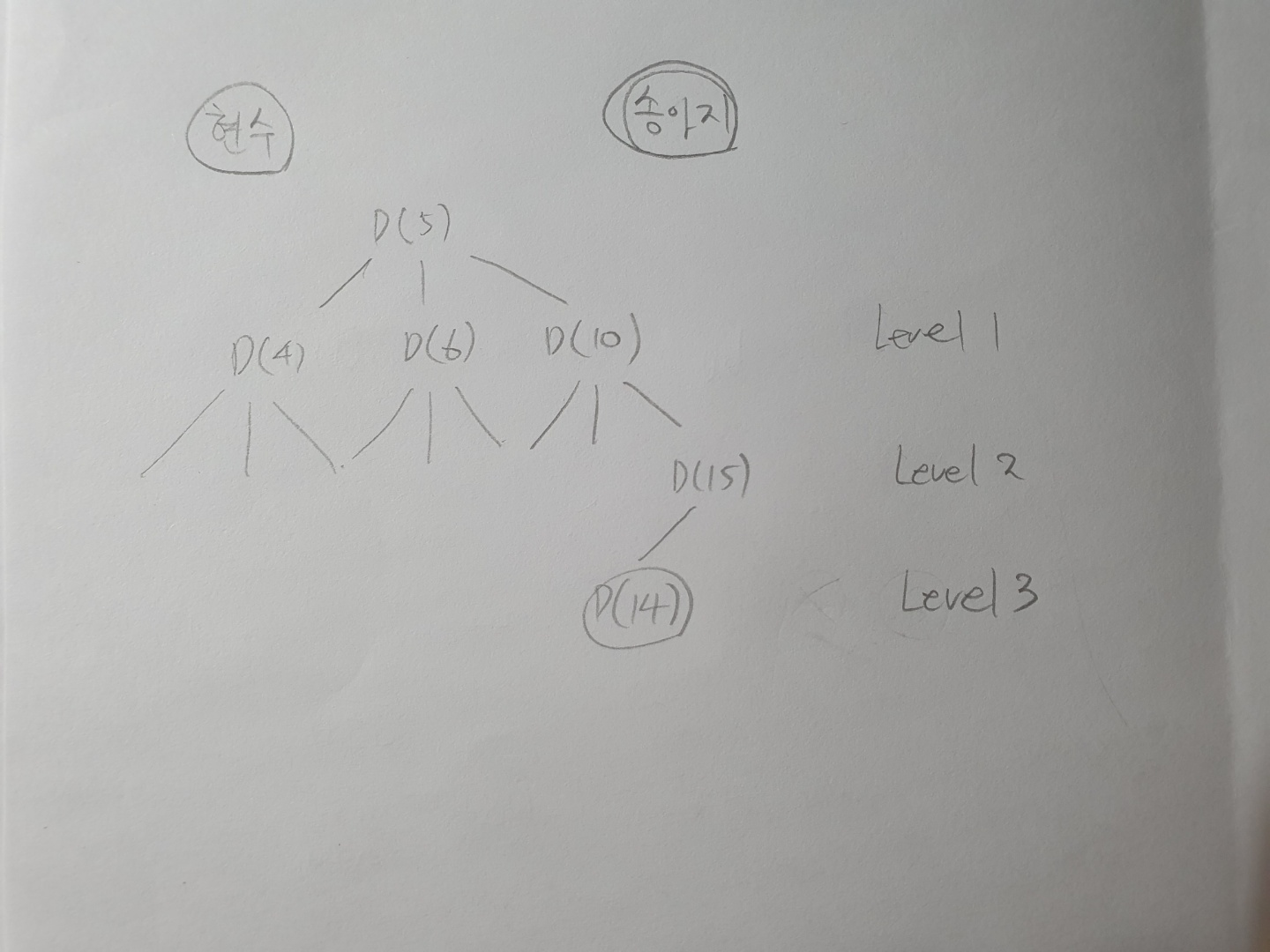
출발점을 처음에 queue에 넣고 -1, 1, 5의 경우의 수를 하니씩 돌면서 송아지의 위치와 같은게 있는지 비교하고 없다면 마찬가지로 기존 값에서 -1, 1, 5를 해주면서 처음으로 찾아지는 값을 그대로 출력해주면 된다.

여기서 문제는 각 node에 level을 어떻게 구현해서 출력하는지가 관건인데 따로 배열을 두개 만들어 해당 값의 인덱스의 거리를 그 전에 노드에 +1을 해주면서 거리를 기억하고 있다가 m과 같은 값이 나오는 순간 그 전에 pop한 값의 거리 값에 +1을 해줘서 출력하는식으로 구현해볼 수 있다.

function solution(s, m) {
  let answer = 0;
  let ch = Array.from({length: 10001}, () => 0);
  let dis = Array.from({length: 10001}, () => 0);
  let queue = [];
  queue.push(s);
  ch[s] = 1;
  dis[s] = 0;
  while (queue.length) {
    let v = queue.shift();
    for (let nx of [v - 1, v + 1, v + 5]) {
      if (nx === m) return dis[v] + 1;
      if (nx > 0 && nx < 10000 && ch[nx] === 0) {
        queue.push(nx);
        ch[nx] = 1;
        dis[nx] = dis[v] + 1;
      }
    }
  }
  return answer;
}