[쇼핑 데이터 분석] chpt5

선형회귀모형

X: 부모의 키, Y: 자녀의 키

이 때, 부모의 키를 통해 자녀의 키를 어떻게 예측 할 수 있을까?

data=pd.read_excel('data3.xlsx')
data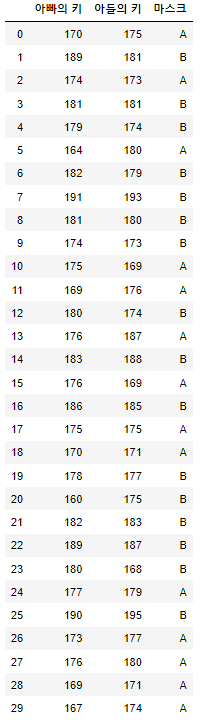

* Train data: 모형을 학습시키는데 사용되는 데이터
* Test data: 학습된 모형을 평가하는데 사용되는 데이터 
* 아래 코드를 이용해 Train data와 Test data를 분리 

train_data=data.iloc[0:20,:]
test_data=data.iloc[20:,:]

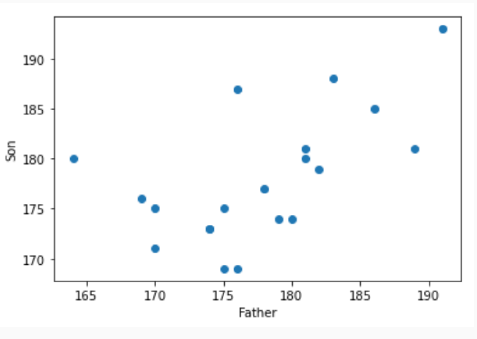
* 산점도를 그려보자

plt.scatter(x=train_data.iloc[:,0], y=train_data.iloc[:,1])
plt.xlabel('Father')
plt.ylabel('Son')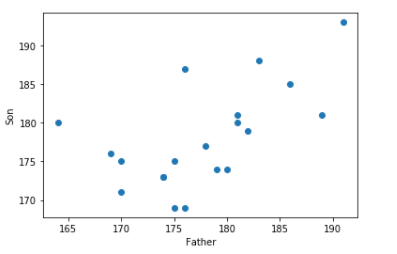

• 아빠의 키를 통해(독립변수 X) -> 자녀의 키 구함(종속변수 Y)
• Train data D={(x1,y1),...,(xn,yn)}, Xi : 독립변수, Yi: 종속변수
• 이 때,
  
  
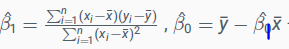
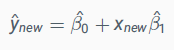
  으로 구할 수 있다.

즉, 아빠의 키 x=170일 때 자녀의 키는? B0+B1*170 =Y으로 구할 수 있다.

* B1^의 분자를 계산해보자

a1=0
for i in range(0,20):
    
    a1 = a1 + ( train_data.iloc[i,0] - train_data.iloc[:,0].mean() )*  ( train_data.iloc[i,1] - train_data.iloc[:,1].mean() )    
a1

[output]
487.0

*B1^의 분모를 계산해보자

a2=0
for i in range(0,20):
    
    a2= a2 + ( train_data.iloc[i,0] - train_data.iloc[:,0].mean()) * ( train_data.iloc[i,0] - train_data.iloc[:,0].mean() )
a2
[output]
878.5499999999997

beta1= a1/a2
beta1
[output]
0.5543224631495078

*B0^을 계산해보자

beta0=train_data.iloc[:,1].mean()-beta1*train_data.iloc[:,0].mean()
beta0

[output]
79.52461442148993

* 부모의 키가 170,180일 떄의 아들의 키를 예측해보자. 

beta0+170*beta1
[output]
173.75943315690625


beta0+180*beta1
[output]
179.30265778840135

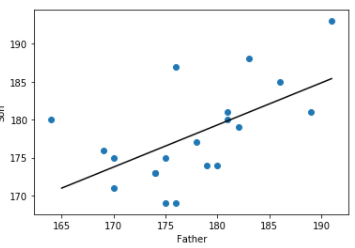
* 산점도와 회의직선모형을 같이 그려보자.

plt.plot([t for t in range(165,192)],[beta0 + t*beta1 for t in range(165,192) ] ,color='black' )
plt.scatter(x=train_data.iloc[:,0], y=train_data.iloc[:,1])
plt.xlabel('Father')
plt.ylabel('Son')

* 이제껏 train data로 선형회귀모형을 만들어봤으니 test data로 모형을 평가해보자
- 모형의 성능 평가

test_data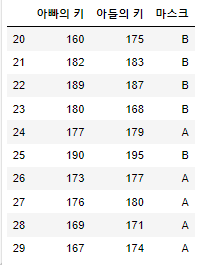

 * test_data에서 아버지의 키를 바탕으로 아들의 키를 예측해보자
 
 pred_son=[]
for i in range(0,10):
    
    pred_son.append(beta0+test_data.iloc[i,0]*beta1)
    
pred_son

[output]

[168.2162085254112,
 180.41130271470035,
 184.2915599567469,
 179.30265778840135,
 177.63969039895284,
 184.8458824198964,
 175.42240054635477,
 177.0853679358033,
 173.20511069375675,
 172.09646576745774]
 
 > 요것이 모델이 예측한 아들의 키 

• 모형평가: 실제 값과 예측 값이 비슷하다면 모형(모델)이 좋다고 할 수 있다.
• 모형 판단 기준
  
  ex) (168-175)^2+(180-183)^2+...
• 위에서 정의된 square error가 작을수록 모형간의 비교에서 모형이 좋다고 할 수 있다. (즉, 실제값과 예측값의 차이가 작을 수록)
• n: test data 개수

* 그렇다면 square error를 바탕으로 우리가 만든 모형을 평가해보자. 

error=0

for i in range(0,10):
    error = error + (pred_son[i]-test_data.iloc[i,1])*(pred_son[i]-test_data.iloc[i,1])

error

[output]
312.2333028484637

* train data에서 이상치를 조사해보자 
아래의 데이터를 보게 되면 이상치로 의심되는 데이터가 존재한다. 

plt.scatter(x=train_data.iloc[:,0], y=train_data.iloc[:,1])
plt.xlabel('Father')
plt.ylabel('Son')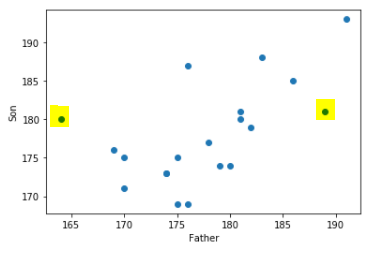

* 이상치로 의심되는 데이터 두개를 제거한 후 모형을 다시 훈련시키자

data.iloc[5,:]
data.iloc[13,:]

a1=0
for i in range(0,20):
    
    if i != 5  | i !=13 : 
        a1 = a1 + ( train_data.iloc[i,0] - train_data.iloc[:,0].mean() )*  ( train_data.iloc[i,1] - train_data.iloc[:,1].mean() )    
        
a1

a2=0
for i in range(0,20):
    
    if i != 5  | i !=13 :
        a2= a2 + ( train_data.iloc[i,0] - train_data.iloc[:,0].mean()) * ( train_data.iloc[i,0] - train_data.iloc[:,0].mean() )
        
a2

beta1= a1/a2
beta1
[output]
0.6238342293766359

ymean= ( sum(train_data.iloc[:,1]) - 180-187 )/18
xmean= (sum(train_data.iloc[:,0]) -  164-176)/18

beta0 = ymean - beta1*xmean
beta0
[output]
66.03447894515938

* 바뀐 데이터로 산점도와 선형회귀모형을 다시 그려보자.

xdata=train_data.iloc[:,0].tolist()
del xdata[5]
del xdata[13]

ydata=train_data.iloc[:,1].tolist()
del ydata[5]
del ydata[13]

plt.plot([t for t in range(165,192)],[beta0 + t*beta1 for t in range(165,192) ] ,color='black' )
plt.scatter(x=xdata, y=ydata)
plt.xlabel('Father')
plt.ylabel('Son')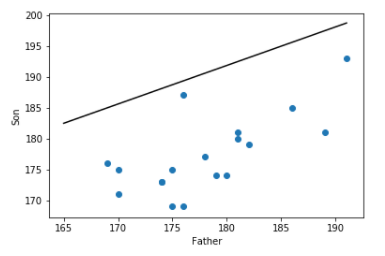

* 새롭게 훈련된 모형을 평가해보자. 


pred_son=[]
for i in range(0,10):
    
    pred_son.append(beta0+test_data.iloc[i,0]*beta1)
    
error=0

for i in range(0,10):
    
    error = error + (pred_son[i]-test_data.iloc[i,1])*(pred_son[i]-test_data.iloc[i,1])
    
error

[output]
368.0851702938408

plt.plot([t for t in range(165,192)],[beta0 + t*beta1 for t in range(165,192) ] ,color='black' )
plt.scatter(x=train_data.iloc[:,0], y=train_data.iloc[:,1])
plt.scatter(x=test_data.iloc[:,0],y=test_data.iloc[:,1])
plt.xlabel('Father')
plt.ylabel('Son')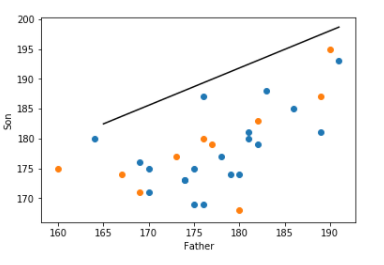

(주황색 점: test data)

• 이상치 제거전 square error = 312 제거후 square error = 368
• 주어진 train data에만 잘 예측하고, test data에 대한 예측력은 떨어질 때 모형이 과적합(overfitting)되었다고 말한다.
• 이상치를 제거한 결과, 모형이 train data에 과적합현상이 발생되어 test data에 대한 예측력이 오히려 안 좋아짐
• 따라서, 항상 "이상치"를 제거하는것이 좋다고 할 순 없다.
  => 상황에 따라 다르게!

선형회귀모형 - 범주형

• 이번엔 예측하는 데이터가 숫자가 아닐 때를 살펴보자.
• 즉, 아빠의 키에 따라서 마스크 A를 사는지, B를 사는지에 대하여 알아보자.

마스크 A를 구매 1, 마스크 B 구매를 0 인 수치형 데이터로 바꿔보자. 

zero_one=[]

for i in range(0,20):
    
    if train_data.iloc[i,2] == 'A':
        
        zero_one.append(1)
        
    else:
        
        zero_one.append(0)
        
pd.DataFrame(zero_one)
[output]
  	0
0	1
1	0
2	1
3	0
4	0
5	1
6	0
7	0
8	0
9	0
10	1
11	1
12	0
13	1
14	0
15	1
16	0
17	1
18	1
19	0
  
* x data = input data를 아빠의 키
  y data = output data를 마스크 A,B에 대한 0,1 데이터로 두었을 때
 선형회귀모형을 적합시켜보자. 
 
a1=0
for i in range(0,20):

        a1 = a1 + ( train_data.iloc[i,0] - train_data.iloc[:,0].mean() )*  ( zero_one[i] - np.mean(zero_one) )   
        
a2=0
for i in range(0,20):

        a2= a2 + ( train_data.iloc[i,0] - train_data.iloc[:,0].mean()) * ( train_data.iloc[i,0] - train_data.iloc[:,0].mean() 
        
beta1= a1/a2
beta1
[output]
-0.05674122133060159

beta0 = np.mean(zero_one) - beta1*train_data.iloc[:,0].mean()
beta0
[output]
10.530077969381372

* 학습된 모형을 바탕으로 y 예측값이 0보다 크면 "1" = 마스크 A 구매
0보다 작으면 "0" = 마스크 B 구매 

classification=[]

for i in range(0,10):
    
    print(beta0+beta1*test_data.iloc[i,0])
    if beta0+beta1*test_data.iloc[i,0] >0 :
        
        classification.append(1)
        
    else: 
        classification.append(0)
        
1.451482556485118
0.20317568721188195
-0.19401286210232804
0.31665812987308506
0.4868817938648906
-0.2507540834329305
0.7138466791872968
0.543623015195493
0.940811564509703
1.0542940071709062

test_data
[output]
  아빠의 키	아들의 키  마스크
20	160	    175	        B
21	182	    183			B
22	189	    187			B
23	180		168			B
24	177		179			A
25	190		195			B
26	173		177			A
27	176		180			A
28	169		171			A
29	167		174			A

classification
[output]
[1, 1, 0, 1, 1, 0, 1, 1, 1, 1]

* 1: 마스크 A, 0:마스크 B
* 즉 10개의 test data 중 7개르 맞추었다. 

위의 모형을 조금 개선해보자.

현재 모형이 키가 189, 190 인 데이터들은 잘 구별하는 반면에 
그 아래의 키를 잘 구분하지 못하는 것으로 보인다

이에 따라 약간의 regulization term을 이용해보자.

train_data
[output]
  아빠의 키	아들의 키  마스크
0	170		175			A
1	189		181			B
2	174		173			A
3	181		181			B
4	179		174			B
5	164		180			A
6	182		179			B
7	191		193			B
8	181		180			B
9	174		173			B
10	175		169			A
11	169		176			A
12	180		174			B
13	176		187			A
14	183		188			B
15	176		169			A
16	186		185			B
17	175		175			A
18	170		171			A
19	178		177			B

* 위의 test_data와 마찬가지로 조정을 그대로 진행해보면

classification=[]

for i in range(0,20):
    print(beta0+beta1*train_data.iloc[i,0])
    if beta0+beta1*train_data.iloc[i,0]  >0 :
        
        classification.append(1)
        
    else: 
        classification.append(0)

[output]
0.8840703431791024
-0.19401286210232804
0.6571054578566962
0.2599169085424844
0.3733993512036875
1.2245176711627117
0.20317568721188195
-0.30749530476353115
0.2599169085424844
0.6571054578566962
0.6003642365260937
0.940811564509703
0.31665812987308506
0.543623015195493
0.14643446588128128
0.543623015195493
-0.023789198110524268
0.6003642365260937
0.8840703431791024
0.43014057253428994

train_label=[]

for i in range(0,20):
    
    if  train_data.iloc[i,2] == 'A' :
        
        train_label.append(1)
        
    else:
        
        train_label.append(0)
        
train_label
[output]
[1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0]
 
classification
[1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1]

> train data에 대한 정확도는 20개 중 12개를 맞추는 상황
> 아빠의 키가 189,190와 같이 비교적 큰 키에 대한 예측은 잘하지만, 
180와 같은 데이터는 예측을 잘 못하는 것으로 보임

* -0.33 으로 제약을 주자. 

classification=[]

for i in range(0,20):
    print(beta0+beta1*train_data.iloc[i,0] -0.33)
    if beta0+beta1*train_data.iloc[i,0] -0.33 >0 :
        
        classification.append(1)
        
    else: 
        classification.append(0)
 
 [output]
0.5540703431791023
-0.5240128621023281
0.32710545785669615
-0.07008309145751562
0.043399351203687486
0.8945176711627116
-0.12682431278811807
-0.6374953047635312
-0.07008309145751562
0.32710545785669615
0.2703642365260937
0.610811564509703
-0.013341870126914956
0.21362301519549304
-0.18356553411871873
0.21362301519549304
-0.3537891981105243
0.2703642365260937
0.5540703431791023
0.10014057253428993

train_label=[]

for i in range(0,20):
    
    if  train_data.iloc[i,2] == 'A' :
        
        train_label.append(1)
        
    else:
        
        train_label.append(0)
        
train_label
[output]
[1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 1, 0]

classification
[output]
[1, 1, 0, 1, 1, 0, 1, 1, 1, 1]

> 20개중 17개를 맞추게 되었다.(모델향상)

* test data에 대한 예측 진행 

test_label=[]

for i in range(0,10):
    
    if  test_data.iloc[i,2] == 'A' :
        
        test_label.append(1)
        
    else:
        
        test_label.append(0)

test_label
[output]
[0, 0, 0, 0, 1, 0, 1, 1, 1, 1]

classification=[]

for i in range(0,10):
    
    print(beta0+beta1*test_data.iloc[i,0] -0.33)
    if beta0+beta1*test_data.iloc[i,0] -0.33 >0 :
        
        classification.append(1)
        
    else: 
        classification.append(0)
[output]    
1.1214825564851179
-0.12682431278811807
-0.5240128621023281
-0.013341870126914956
0.1568817938648906
-0.5807540834329306
0.3838466791872968
0.21362301519549304
0.610811564509703
0.7242940071709061

classification
[output]
[1, 0, 0, 0, 1, 0, 1, 1, 1, 1]

> 10개 중 9개를 맞추었고 성능이 대폭 향상

군집화(clustering)

군집화란? label(y값)이 없는 데이터를 서로 관련있는 데이터끼리 묶는 것
대표적인 알고리즘 예시로는 k-means(k-평균) clustering이 있다.

* 아래와 같은 데이터가 있다. 

x=[1,2,2,7,5,6,5,6,7]
y=[1,2,1,8,8,9,2,3,3]
plt.scatter(x,y,color=['black'])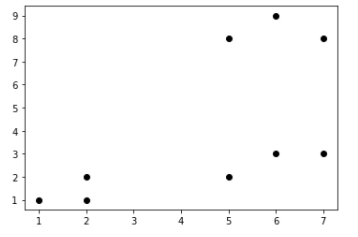

* 주어진 데이터 3개(k=3)를 군집으로 군집화할 때, 주어진 데이터에서 랜덤으로 3개를 선택한다. 

plt.scatter(x,y,color=['red','black','black','red','black','black','red','black','black'])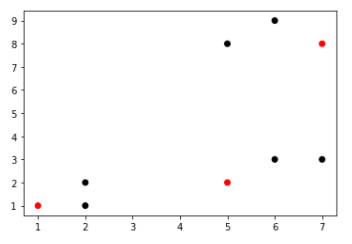

* 선택된 데이터와 거리가 가장 가까운 데이터들을 모두 모은다. (각 군집으로 분류된 것)

plt.scatter(x,y,color=['pink','pink','pink','blue','blue','blue','green','green','green'])

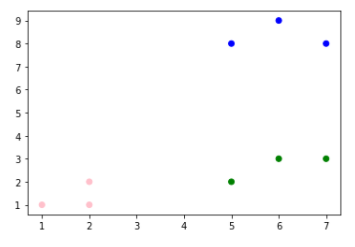
* 각 군집에서의 평균값에 해당되는 점을 만들고, 이 점들과 가장 가까운 점들을 다시 군집

* 이 작업을 계속 반복한다. 

x=[1,2,2,1.7,5,7,5,6,5,6,7,6]
y=[1,2,1,1.3,8,8,9,8.3,2,3,3,2.3]

plt.scatter(x,y,color=['pink','pink','pink','black','blue','blue','blue','black','green','green','green','black'])

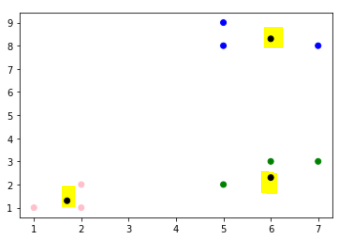
* 노란 부분이 각 군집의 평균 


* 아래 코드를 이용해 데이터를 불러오자. (전처리도 진행)
customer_data=pd.read_csv('marketing_campaign.csv')
customer_data

cust_data=[]

for i in range(0,2240):
    
    a=customer_data.iloc[i,:][0].split('\t')
    cust_data.append(a)
    
cust_data=pd.DataFrame(cust_data)
cust_data.columns=customer_data.columns[0].split('\t')

cust_data

[output]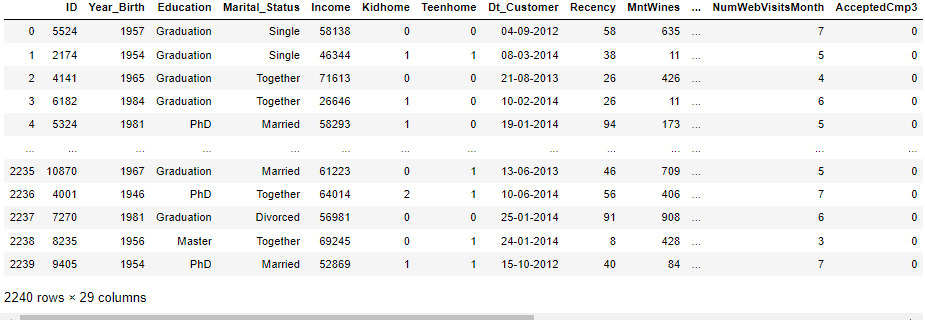

cust_data.iloc[0,:]
[output]

ID                           5524
Year_Birth                   1957
Education              Graduation
Marital_Status             Single
Income                      58138
Kidhome                         0
Teenhome                        0
Dt_Customer            04-09-2012
Recency                        58
MntWines                      635
MntFruits                      88
MntMeatProducts               546
MntFishProducts               172
MntSweetProducts               88
MntGoldProds                   88
NumDealsPurchases               3
NumWebPurchases                 8
NumCatalogPurchases            10
NumStorePurchases               4
NumWebVisitsMonth               7
AcceptedCmp3                    0
AcceptedCmp4                    0
AcceptedCmp5                    0
AcceptedCmp1                    0
AcceptedCmp2                    0
Complain                        0
Z_CostContact                   3
Z_Revenue                      11
Response                        1
Name: 0, dtype: object

* 위의 cust_data에서 Dt_customer data를 제거하자.

cust_data=cust_data.drop('Dt_Customer',axis=1)

cust_data_new=cust_data.iloc[:,1:]
cust_data_new.index=cust_data.iloc[:,0]

cust_data_new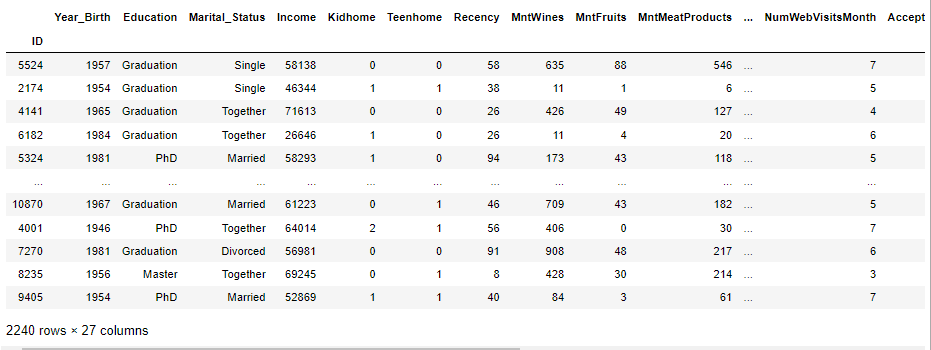

* 이번에는 Year_brith, Education, Marital_status 를 제외하고 나머지 Data를 이용하여 군집화(Clustering)을 진행해보자.
* income data가 missing인 데이터들 제거

clustering_data=cust_data_new.iloc[:,3:]
clustering_data.loc[clustering_data['Income'] == '']
clustering_data=clustering_data.loc[clustering_data['Income'] != '']

* 데이터 전체 타입(type)을 정수(int)로 바꾸어서 사직연산이 가능하게 하자. 

clustering_data=clustering_data.astype(int)

* K-means는 단위에 민감하므로, 표준화로 데이터 전처리를 진행해보자.
* 총합을 각각 나눠줌 > 비율로 만들어주기 위해

sum1=[]

for i in range(0,24):
    
    sum1.append(clustering_data.iloc[:,i].sum())
    

for i in range(0,24):
    
    clustering_data.iloc[:,i] = clustering_data.iloc[:,i] / sum1[i]
    
clustering data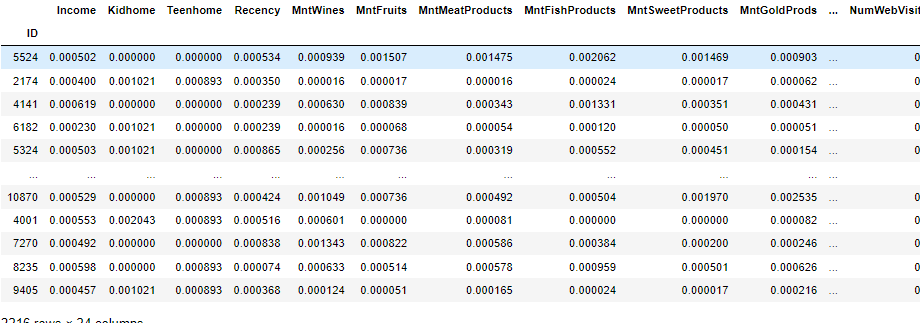

* k-means 군집화 패키지 이용

from sklearn.cluster import KMeans
km=KMeans(n_clusters=5)
km.fit(clustering_data)

* k-means 군집화를 통한 군집된 데이터의 class를 의미

label=pd.DataFrame(km.labels_)
label.columns=['label']
label.index=clustering_data.index
label

	label
ID	
5524	2
2174	2
4141	2
6182	2
5324	2
...	...
10870	2
4001	0
7270	2
8235	2
9405	2

* 원래 데이터에서 각 데이터가 군집된 class를 추가

cluster_label_data=pd.concat([cust_data_new, label],axis=1)
cluster_label_data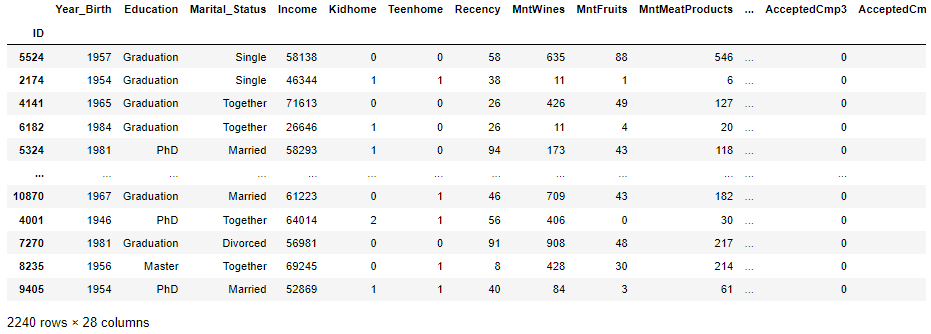

* 각 그룹 0부터 4까지 조사
* class 0으로 분류된 데이터들 저장

group0=cluster_label_data.loc[cluster_label_data.iloc[:,-1] == 0]
group0

* group0에 모여있는 데이터들의 특성

group0.iloc[:,0].astype(int).mean()
[output]
1971.0212765957447

group0.iloc[:,1].value_counts()
Graduation    67
PhD           35
Master        20
2n Cycle      13
Basic          6
Name: Education, dtype: int64

group0.iloc[:,2].value_counts()
Married     54
Single      35
Together    31
Divorced    17
Widow        3
Alone        1
Name: Marital_Status, dtype: int64

group0.iloc[:,3].astype(int).mean()
46773.21985815603

* class 1으로 분류된 데이터들 저장
group1=cluster_label_data.loc[cluster_label_data.iloc[:,-1] == 1]

group1.iloc[:,0].astype(int).mean()
1968.858319604613

group1.iloc[:,1].value_counts()
Graduation    912
PhD           388
Master        308
2n Cycle      165
Basic          48
Name: Education, dtype: int64

group1.iloc[:,2].value_counts()
Married     700
Together    473
Single      386
Divorced    194
Widow        63
Alone         2
YOLO          2
Absurd        1
Name: Marital_Status, dtype: int64

group1.iloc[:,3].astype(int).mean()
49405.962657880285

등 으로 각 그룹에 대한 특성을 파악할 수 있다.