최근 VELOG 회고록
프로젝트가 끝나고
알고리즘에 대해서 고민을 하다보니 알고리즘을 풀 때
데이터 처리를 하기 위해서 어떤 자료구조를 접근해서 시간복잡도를 효율적으로 줄이는 것이 관건이라고 생각했다.
접근방식을 알아보니 생각보다 많은 개념방식들이 있었고
한 문제를 다 다르게 접근할 수 있다는 것을 알게 되었는데
오늘의 문제가 바로 그 부분을 깨달게 된 점이였던 것 같다.
백준 2747번 피보나치 수는 2가지 방식으로 풀 수 있다.
1. Dynamic Programming (동적)
Dynamic Programming이란?
문제들을 매번 재계산하지 않고 값을 저장해두었다가 재사용하는 기법이다.
최적화 이론의 한 기술이며, 특정 범위까지의 값을 구하기 위해서 그것과 다른 범위까지의 값을 이용하여 효율적으로 값을 구하는 알고리즘 설계 기법이다.
배열을 선언 한 후 for문으로 돌면서 값을 넣어주면 코드가 완성이 된다.
C++로 풀었기때문에 문제의 시간이나 메모리를 많이 잡아 먹지 않았다.
그리고 찾아보니 DP로 풀면 메모리가 덜 잡아먹어서 시간을 최적화 할 수 있다고 한다.
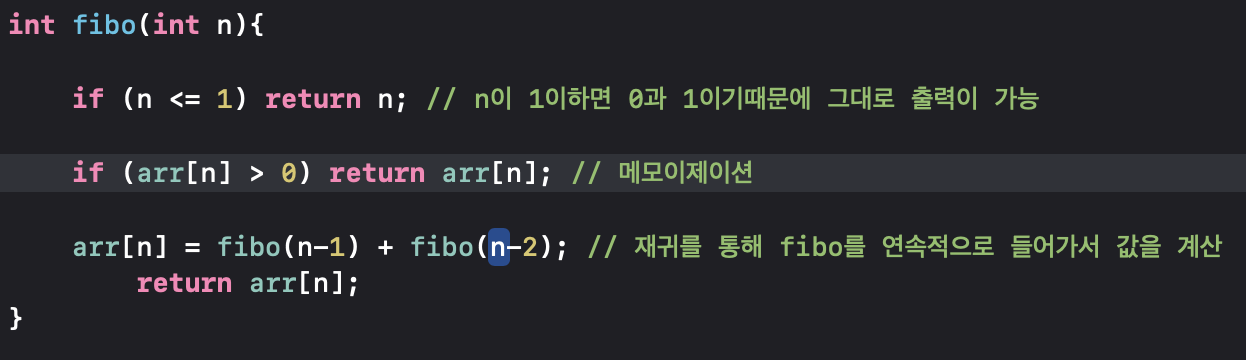
2. Recursive (재귀)
Recursive란?
함수 안에 자신의 함수를 다시 호출하는 함수를 의미한다. 이러한 재귀함수는 자신의 로직을 내부적으로 반복하다가, 일정한 조건이 만족되면 함수를 이탈하여 결과를 도출한다.
재귀로 문제를 풀면서 바로 이부분에서 새로운 개념을 알게 되었는데 그게 바로
Memoization이다.
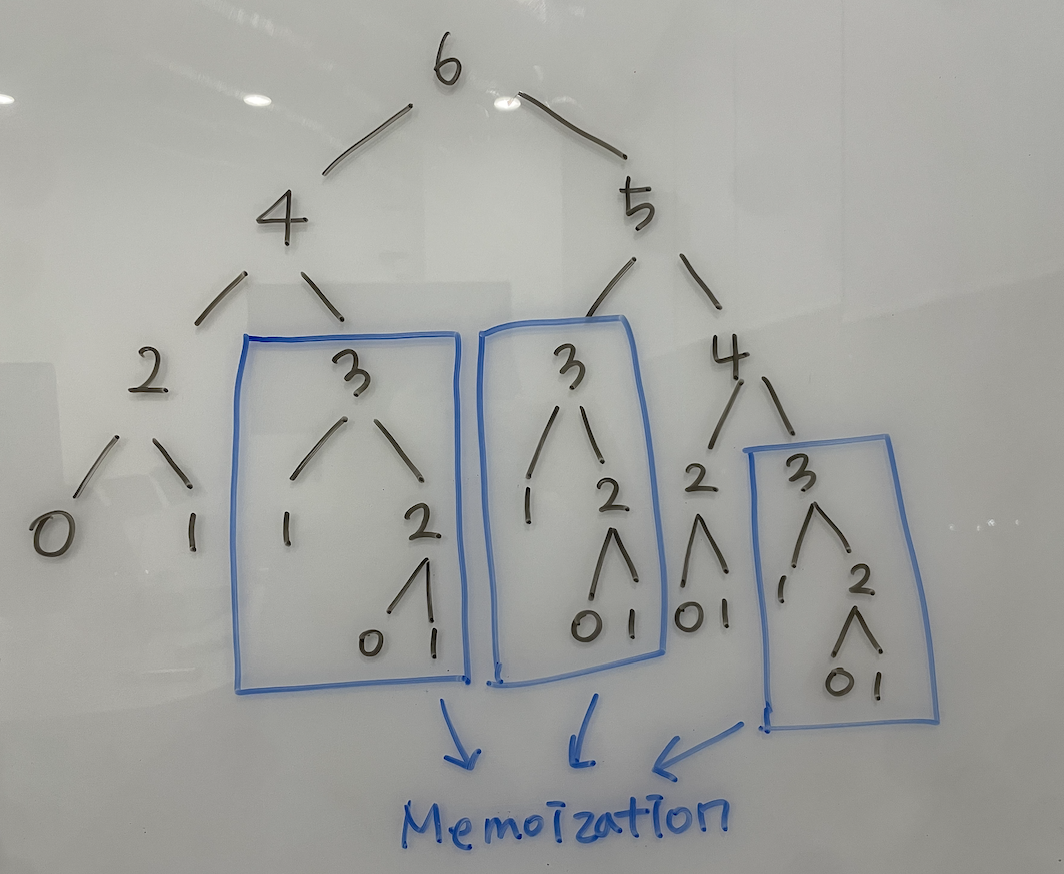
Memoization
이해를 돕기 위해 그림과 함께 설명을 하자면
중복적으로 데이터를 처리해야되는 부분을 처리하는 것을 메모이제이션이라고한다.
이런 중복적인 데이터들을 값에 저장해서 불러오는 방식으로 처리를 하면 시간복잡도에서 엄청 줄어드는 것을 알 수 있다.