C2W1A1 Initialization

좋은 신경망을 만드려면 초기화를 잘 해야한다.
Zero, random, He 초기화를 해보고, 각각 어떤 결과를 내는지 살펴보자

---

준비

import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from public_tests import *
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec

%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

# load image dataset: blue/red dots in circles
train_X, train_Y, test_X, test_Y = load_dataset()

---

다음은 3층 신경망 모델이다.
초기화 방법을 바꾸기 위해, initialization = "zeros"/"random"/"he" 중 하나를 설정한다.

def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):
    """
    Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.
    
    Arguments:
    X -- input data, of shape (2, number of examples)
    Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples)
    learning_rate -- learning rate for gradient descent 
    num_iterations -- number of iterations to run gradient descent
    print_cost -- if True, print the cost every 1000 iterations
    initialization -- flag to choose which initialization to use ("zeros","random" or "he")
    
    Returns:
    parameters -- parameters learnt by the model
    """
        
    grads = {}
    costs = [] # to keep track of the loss
    m = X.shape[1] # number of examples
    layers_dims = [X.shape[0], 10, 5, 1]
    
    # Initialize parameters dictionary.
    if initialization == "zeros":
        parameters = initialize_parameters_zeros(layers_dims)
    elif initialization == "random":
        parameters = initialize_parameters_random(layers_dims)
    elif initialization == "he":
        parameters = initialize_parameters_he(layers_dims)

    # Loop (gradient descent)

    for i in range(num_iterations):

        # Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.
        a3, cache = forward_propagation(X, parameters)
        
        # Loss
        cost = compute_loss(a3, Y)

        # Backward propagation.
        grads = backward_propagation(X, Y, cache)
        
        # Update parameters.
        parameters = update_parameters(parameters, grads, learning_rate)
        
        # Print the loss every 1000 iterations
        if print_cost and i % 1000 == 0:
            print("Cost after iteration {}: {}".format(i, cost))
            costs.append(cost)
            
    # plot the loss
    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()
    
    return parameters

---

Zero Initialization

# GRADED FUNCTION: initialize_parameters_zeros 

def initialize_parameters_zeros(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    parameters = {}
    L = len(layers_dims)            # number of layers in the network
    
    for l in range(1, L):
        parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1]))
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
        
    return parameters

매개변수를 모두 0으로 초기화한다.
위 함수의 실행 결과 매개변수 값들은 다음과 같다

W1 = [[0. 0. 0.]
      [0. 0. 0.]]
b1 = [[0.]
      [0.]]
W2 = [[0. 0.]]
b2 = [[0.]]

아래 코드블럭을 실행해 15000번 반복 훈련시킨다

parameters = model(train_X, train_Y, initialization = "zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

훈련 결과는 아래와 같다. 반복해도 비용이 전혀 줄어들지 않는다.

On the train set:
Accuracy: 0.5
On the test set:
Accuracy: 0.5

초기화된 가중치와 편향이 모두 0이라면, 입력 데이터에 가중치를 곱한 결과는 0 벡터가 된다. 이를 ReLU 활성화 함수에 넣으면 결과는 항상 0이다.

$a = ReLU(z) = max(0, z) = 0$

분류층에서는 시그모이드를 사용하므로, 입력과 관계없이 항상 y_pred=0.5로 예측한다.

$\sigma(z) = \frac{1}{ 1 + e^{-(z)}} = \frac{1}{2} = y_{pred}$

모든 샘플에서 0.5의 확률로 True를 예측하고, 손실함수 계산 시 실제값과 예측값이 모두 0.5로 동일해진다. 따라서 손실함수로 가중치를 학습시키지 못하게 된다.

손실함수:
$\mathcal L(a, y) = - y \ln(y_{pred}) - (1-y) \ln(1-y_{pred})$

y=1, y_pred=0.5인 경우:
$\mathcal{L}(0, 1) = - (1) \ln(\frac{1}{2}) = 0.6931471805599453$

y=0, y_pred=0.5인 경우:
$\mathcal{L}(0, 0) = - (1) \ln(\frac{1}{2}) = 0.6931471805599453$

이처럼 실제값 y에 상관없이 같은 Loss 값이 계산된다. 그러므로 w가 업데이트되지 못하고 같은 값에 머무른다.
❗신경망의 가중치가 모두 동일한 값을 가지면, 각 유닛이 동일한 방식으로 학습되어 동일한 값을 출력하게 된다. (대칭성)

✅ 대칭성을 깨기 위해, $W^{[l]}$은 무작위로 초기화해야 한다
✅ $b^{[l]}$는 0으로 초기화해도 된다

---

Random initialization

# GRADED FUNCTION: initialize_parameters_random

def initialize_parameters_random(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    np.random.seed(3)               # This seed makes sure your "random" numbers will be the as ours
    parameters = {}
    L = len(layers_dims)            # integer representing the number of layers
    
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * 10
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
        
    return parameters

이번에는 매개변수를 무작위로 초기화해보자
아까와 같이 15000번 반복하여 신경망을 학습시킨 결과는 다음과 같다

parameters = model(train_X, train_Y, initialization = "random")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)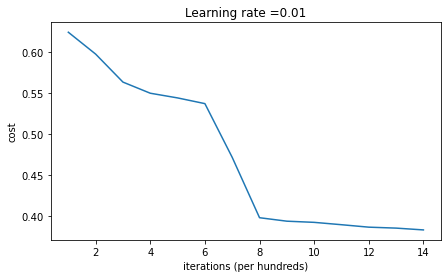

On the train set:
Accuracy: 0.83
On the test set:
Accuracy: 0.86

이번에는 대칭성을 깼으므로 더 정확한 결과가 나왔다.
예측값들도 모두 0인 문제도 해결되었다.

plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

✅ 가중치를 너무 큰 값으로 초기화하면 학습이 잘 되지 않는다.
그렇다면 얼마나 작은 값으로 초기화해야할까?
numpy.random.rand()은 균일분포(Uniform distribution, 0~1 값들이 동일한 확률로 발생)
numpy.random.randn()은 정규분포(Normal/Gaussian distribution)에서 숫자를 생성한다.

randn을 사용하면 가중치가 극단값에 가까워지는 것을 피할 수 있다.
(예를 들어, 시그모이드 함수에서 0이나 1 근처의 기울기는 너무 작기 때문에 학습이 매우 느리게 진행된다. 이와 같은 상황을 피할 수 있다.)

---

He Initialization

Xavier initialization은
sqrt(1./layers_dims[l-1])

이와 비슷하게, He initialization은
sqrt(2./layers_dims[l-1])를 사용한다.

# GRADED FUNCTION: initialize_parameters_he

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims) - 1 # integer representing the number of layers
     
    for l in range(1, L + 1):    
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1]) * np.sqrt(2./layers_dims[l-1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
  
    return parameters

Random initialization에서 가중치를 초기화할 때 randn()에 10을 곱했었다
이번에는 np.sqrt(2./layers_dims[l-1])를 곱한다

parameters = model(train_X, train_Y, initialization = "he")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)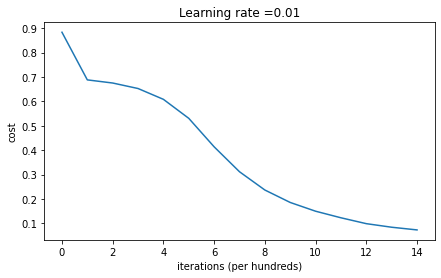

On the train set:
Accuracy: 0.9933333333333333
On the test set:
Accuracy: 0.96

He 초기화를 사용한 모델은 파란 점과 빨간 점을 매우 잘 구분했다.

plt.title("Model with He initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)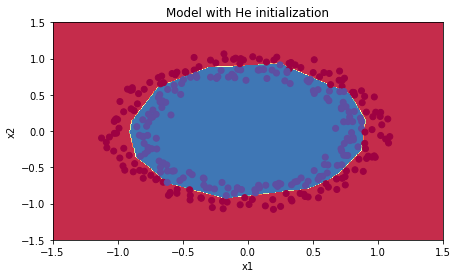

---

결론

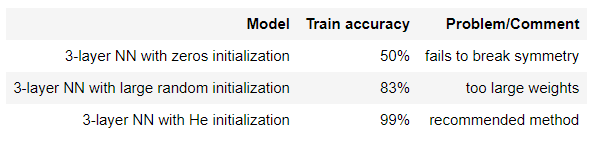
어떻게 초기화하느냐에 따라 매우 다른 결과가 나온다
무작위로 초기화하면 대칭성을 깰 수 있고, 각 유닛이 다르게 학습할 수 있게 된다
너무 큰 값으로 초기화하면 안된다