[제로베이스] 데이터 사이언스 15기 - (05-18 기초 수학 스터디노트)

오늘 수강한 강의 - 기초 수학 문제풀이 (31 ~ 45)

31 약수와 소수 ~ 45 확률

약수와 소수

• 100부터 1000사이의 난수에 대해서 약수, 소수, 그리고 소인수를 출력하는 프로그램

import random

rNum = random.randint(100, 1000)
print('rNum: {}'.format(rNum))

for num in range(1, rNum+1):
    soinsuFlag = 0

    if rNum % num == 0:
        print('[약수]: {}'.format(num))
        soinsuFlag += 1

    if num != 1:
        flag = True
        for n in range(2, num):
            if num % n == 0:
                flag = False
                break
        if(flag):
            print('[소수]: {}'.format(num))
            soinsuFlag += 1

    if soinsuFlag >= 2:
        print('[소인수]: {}'.format(num))

소인수와 소인수 분해

• 100부터 1000사이의 난수를 소인수 분해를 하고 각각의 소인수에 대한 지수를 출력하는 프로그램

import random

rNum = random.randint(100, 1000)
print('rNum: {}'.format(rNum))
soinsuList = []

n = 2
while n <= rNum:
    if rNum % n == 0:
        print('소인수: {}'.format(n))
        soinsuList.append(n)
        rNum /= n
    else:
        n += 1
print('soinsuList: {}'.format(soinsuList))

tempNum = 0
for s in soinsuList:
    if tempNum != s:
        print('{}\'s count: {}'.format(s, soinsuList.count(s)))
        tempNum = s

최대공약수

• 100부터 1000사이의 2개의 난수에 대해서 공약수와 최대공약수를 출력하고, 서로소인지 출력하는 프로그램

import random
rNum1 = random.randint(100, 1000)
rNum2 = random.randint(100, 1000)
print('rNum1: {}'.format(rNum1))
print('rNum2: {}'.format(rNum2))

maxNum = 0
for n in range(1, (min(rNum1, rNum2)+1)):
    if rNum1 % n == 0 and rNum2 % n == 0:
        print('공약수: {}'.format(n))
        maxNum = n

print('최대공약수: {}'.format(maxNum))

if maxNum == 1:
    print('{}과 {}는 서로소'.format(rNum1, rNum2))

최소공배수

• 100부터 1000사이의 2개의 난수에 대해서 최대공약수와 최소공배수를 출력하는 프로그램

최소공배수 = (rNum1 * rNum2) // 최대공약수

import random
rNum1 = random.randint(100, 1000)
rNum2 = random.randint(100, 1000)
print('rNum1: {}'.format(rNum1))
print('rNum2: {}'.format(rNum2))

maxNum = 0
for n in range(1, (min(rNum1, rNum2)+1)):
    if rNum1 % n == 0 and rNum2 % n == 0:
        print('공약수: {}'.format(n))
        maxNum = n

print('최대공약수: {}'.format(maxNum))

minNum = (rNum1 * rNum2) // maxNum
print('최소공배수: {}'.format(minNum))

진법

• 사용자가 입력한 수를 이용해서, 다음 내용에 따라 진법 변환하는 코드를 작성해보자
  

dNum = int(input('10진수 입력: '))

• 10진수 -> 2, 8, 16진수

print('2진수: {}'.format(bin(dNum)))
print('8진수: {}'.format(oct(dNum)))
print('16진수: {}'.format(hex(dNum)))

• X진수 -> 10진수

print('2진수(0b10101) -> 10진수({})'.format(int('0b10101', 2)))
print('8진수(0o135) -> 10진수({})'.format(int('0o135', 8)))
print('16진수(0x5f) -> 10진수({})'.format(int('0x5f', 16)))

• X진수 -> X진수

print('2진수(0b10101) -> 8진수({})'.format(oct(0b10101)))
print('2진수(0b10101) -> 10진수({})'.format(int(0b10101)))
print('2진수(0b10101) -> 16진수({})'.format(hex(0b10101)))

print('8진수(0o675) -> 2진수({})'.format(bin(0o675)))
print('8진수(0o675) -> 10진수({})'.format(int(0o675)))
print('8진수(0o675) -> 16진수({})'.format(hex(0o675)))

print('16진수(0x45d) -> 2진수({})'.format(bin(0x45d)))
print('16진수(0x45d) -> 8진수({})'.format(oct(0x45d)))
print('16진수(0x45d) -> 10진수({})'.format(int(0x45d)))

등차수열

• 다음 수열의 일반항을 구하고 n번째항의 값과 합을 구하는 프로그램
  

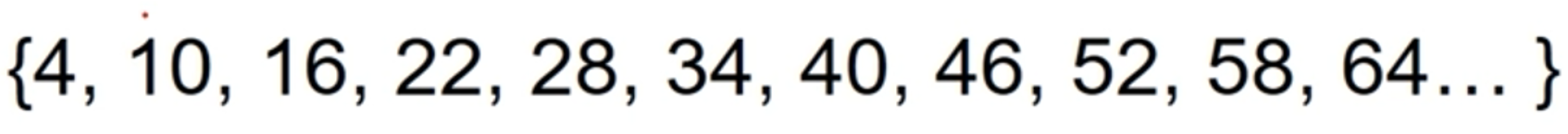
반복문 사용

inputA1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('{}번째 항의 값: {}'.format(n, valueN))
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    valueN += inputD
    sumN += valueN
    print('{}번째 항의 값: {}'.format(n, valueN))
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))
print('{}번째 항까지의 합: {}'.format(inputN, sumN))

등차 수열(일반항) 공식: an = a1 + (n-1) * d

valueN = inputA1 + (inputN-1) * inputD
print('{}번째 항의 값: {}'.format(inputN, valueN))

등차 수열(합) 공식: sn = n(a1 + an) / 2

sumN = inputN * (inputA1 + valueN) / 2
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))

등비수열

• 다음 수열의 일반항을 구하고 n번째항의 값과 합을 구하는 프로그램
  

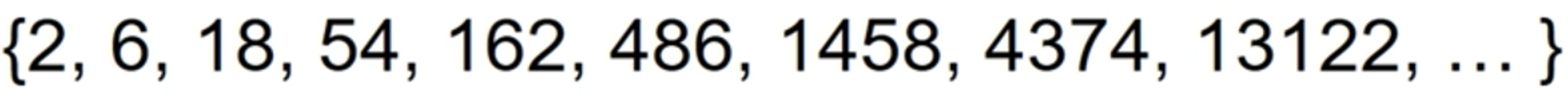
반복문 사용

inputA1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('{}번째 항의 값: {}'.format(n, valueN))
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    valueN *= inputR
    sumN += valueN
    print('{}번째 항의 값: {}'.format(n, valueN))
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))
print('{}번째 항까지의 합: {}'.format(inputN, sumN))

등비 수열(일반항) 공식: an = a1 * r^(n-1)

valueN = inputA1 * (inputR ** (inputN-1))
print('{}번째 항의 값: {}'.format(inputN, valueN))

등비 수열(합) 공식: sn = a1 * (1 - r^n) / (1-r)

sumN = inputA1 * (1 - (inputR ** inputN)) / (1 - inputR)
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))

시그마

• 첫 째날 쌀 두톨을 받고 둘째 날부터는 하루 전의 2배의 해당하는 쌀을 받는다고 할 때, 30일째 되는 날 받게 되는 쌀의 개수를 수열과 시그마로 나타내고 이를 출력하는 프로그램을 만들어 보자
  

반복문 사용

inputA1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputA1
        sumN += valueN
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    valueN *= inputR
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1

print('{}번째 항까지의 합: {}'.format(inputN, format(sumN, ',')))

등비 수열(합) 공식: sn = a1 * (1 - r^n) / (1-r)

sumN = inputA1 * (1 - (inputR ** inputN)) / (1 - inputR)
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))

계차수열

• 다음 수열의 일반항을 구하고, n항의 값을 출력하는 프로그램
  

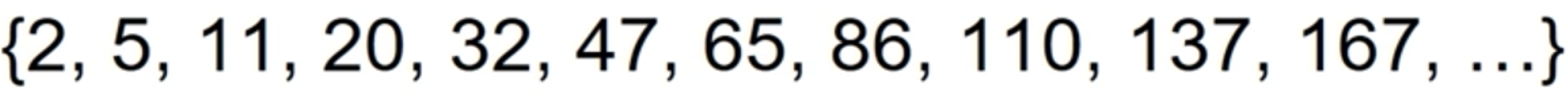
(3n^2 - 3n + 4)/2 = an

inputA1 = int(input('a1 입력: '))
inputN = int(input('an 입력: '))

valueN = ((3 * inputN ** 2) - (3 * inputN) + 4) / 2
print('an의 {}번째 항의 값: {}'.format(inputN, int(valueN)))

피보나치 수열

• 피보나치 수열에서 n항의 값과 n항까지의 합을 출력하는 프로그램

inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
valuePreN2 = 0
valuePreN1 = 0

n = 1
while n <= inputN:
    if n == 1 or n == 2:
        valueN = 1
        valuePreN2 = valueN
        valuePreN1 = valueN
        sumN += valueN
        n += 1
    else:
        valueN = valuePreN2 + valuePreN1
        valuePreN2 = valuePreN1
        valuePreN1 = valueN
        sumN += valueN
        n += 1

print('{}번째 항의 값: {}'.format(inputN, valueN))
print('{}번째 항까지의 합: {}'.format(inputN, sumN))

팩토리얼

• 팩토리얼 프로그램을 만들되, 반복문을 이용한 함수와 재귀 함수를 이용해서 구현해보고 또한, 파이썬에서 제공하는 모듈도 사용해 보자

반복문

def facFun1(n):
    fac = 1
    for n in range(1, (n + 1)):
        fac *= n
    return fac

num = int(input('input number: '))
print('{}!: {}'.format(num, facFun1(num)))

재귀 함수

def facFun2(n):
    if n == 1:
        return n
    return n * facFun2(n-1)

num = int(input('input number: '))
print('{}!: {}'.format(num, facFun2(num)))

math 모듈

import math

num = int(input('input number: '))
print('{}!: {}'.format(num, math.factorial(num)))

군 수열

• 다음 수열을 보고 수열의 합이 최고 100을 초과하는 n번째 항의 값과 n을 출력하는 프로그램
  

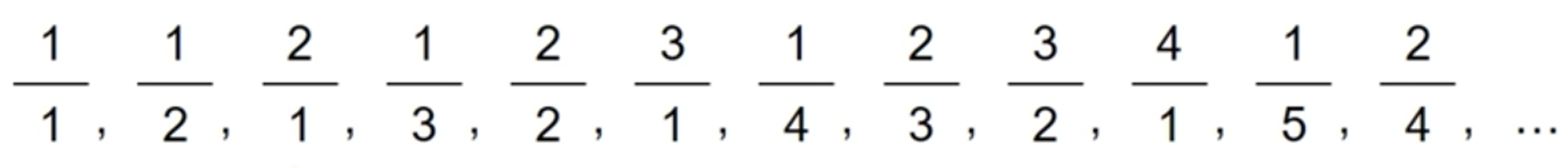
flag = True
n = 1
nCnt = 1
searchNC = 0
searchNP = 0
sumN = 0

while flag:
    for i in range(1, (n + 1)):
        print('{}/{} '.format(i, (n - i + 1)), end='')
        sumN += (i / (n - i + 1))
        nCnt += 1

        if sumN > 100:
            searchNC = i
            searchNP = n - i + 1
            flag = False
            break
    print()
    n += 1

print('수열의 합이 최초 100을 초과하는 항, 값, 합: {}항, {}/{}, {}'.format(nCnt, searchNC, searchNP, sumN))

순열

• 파이썬을 이용하여 다음 순열들의 값을 구하는 프로그램
  

numN = int(input('numN 입력: '))
numR = int(input('numR 입력: '))
result = 1

for n in range(numN, (numN - numR), -1):
    print('n : {}'.format(n))
    result = result * n

print('result: {}'.format(result))

• 카드 7장을 일렬로 나열하되 2, 4, 7번 카드가 서로 이웃하도록 나열하는 모든 경우의 수를 구하는 프로그램
  

2, 4, 7을 하나로 보고 5! x 3!

fNum1 = int(input('factorial1 입력: '))
result1 = 1

for n in range(fNum1, 0, -1):
    result1 *= n
print('result1: {}'.format(result1))

fNum2 = int(input('factorial2 입력: '))
result2 = 1

for n in range(fNum2, 0, -1):
    result2 *= n
print('result: {}'.format(result2))

print('모든 경우의 수: {}'.format(result1 * result2))

조합

• 파이썬을 이용해서 다음 조합들의 값을 구하는 프로그램
  

numN = int(input('numN 입력: '))
numR = int(input('numR 입력: '))
resultP = 1
resultR = 1
resultC = 1

for n in range(numN, (numN - numR), -1):
    resultP *= n
print('resultP: {}'.format(resultP))

for n in range(numR, 0, -1):
    resultR *= n
print('resultR: {}'.format(resultR))

resultC = int(resultP / resultR)
print('resultC: {}'.format(resultC))

• 카드 7장 중 3장을 선택했을 때 3, 4, 5가 동시에 선택될 수 있는 확률
  

numN = int(input('numN 입력: '))
numR = int(input('numR 입력: '))
resultP = 1
resultR = 1
resultC = 1

for n in range(numN, (numN - numR), -1):
    resultP *= n
print('resultP: {}'.format(resultP))

for n in range(numR, 0, -1):
    resultR *= n
print('resultR: {}'.format(resultR))

resultC = int(resultP / resultR)
print('resultC: {}'.format(resultC))

%

result = (1/resultC) * 100
print('{}%'.format(round(result, 2)))

확률

• 박스에 '꽝'이 적힌 종이가 6장 있고, '선물'이 적힌 종이가 4장이 있을 때, 파이썬을 이용하여 '꽝' 3장과 '선물' 3장을 뽑는 확률을 출력
  

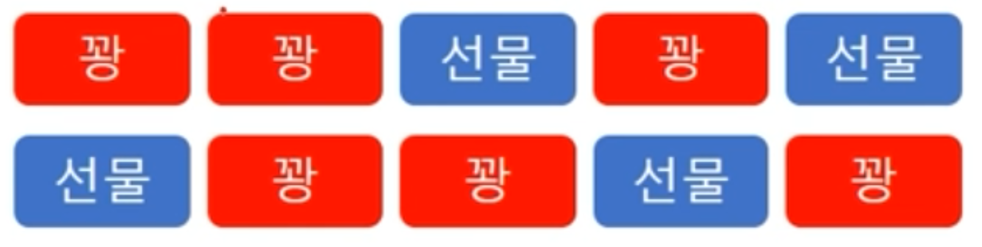
• (순서가 상관없으므로 조합)
  10C6 -> 전체 경우의 수
  6C3 -> 꽝 6장 중 3개 선택 경우의 수
  4C3 -> 선물 4개중 3개 선택 경우의 수
  6C3 x 4C3 / 10C6

def proFun():
    numN = int(input('numN 입력: '))
    numR = int(input('numR 입력: '))
    resultP = 1
    resultR = 1
    resultC = 1

순열(P)

    for n in range(numN, (numN - numR), -1):
        resultP *= n
    print('resultP: {}'.format(resultP))

R(f)

    for n in range(numR, 0, -1):
        resultR *= n
    print('resultR: {}'.format(resultR))

조합(C)

    resultC = int(resultP / resultR)
    print('resultC: {}'.format(resultC))
    return resultC

sample = proFun()
print('sample: {}'.format(sample))
event1 = proFun()
print('event1: {}'.format(event1))
event2 = proFun()
print('event1: {}'.format(event2))

probability = (event1 * event2) / sample
print('probability: {}%'.format(round(probability * 100, 2)))

재미있었던 부분

기초수학 강의에서 들을때는 이해가 안가던 군 수열이 문제풀이를 하면서 조금 이해가 되었고 순열, 조합 부분을 이용한 확률 부분이 가장 재미있었다

어려웠던 부분

계차수열 부분이 항상 파이썬을 이용할때 헷갈리고 막상 혼자 코드를 만들어 보려고 하면 막힐때가 있어서 어려웠다

느낀점 및 내일 학습 계획

강의에서도 이해를 위해 반복문을 사용한다고 하니
공식부분은 계속 보고 외워야겠다
내일은 자료구조 강의를 볼 예정이다