[제로베이스] 데이터 사이언스 15기 - (05-16 기초 수학 스터디노트)

오늘 수강한 강의 - 기초 수학 (01 ~ 20)

01 약수와 소수 ~ 06 최대 공약수

약수

• 어떤 수를 나누어 떨어지게 하는 수

소수

• 1과 자신만을 약수로 가지는 수 (1 제외)

(실습) 1부터 30까지의 숫자 중 5로 나눈 몫과 나머지가 모두 소수인 숫자들을 찾아보자

1) 몫으로 나올 수 있는 소수를 찾는다
2, 3, 5
2) 5 x 몫에 5보다 작은 소수를 더한다
2 x 5 + 2, 2 x 5 + 3
3 x 5 + 2, 3 x 5 + 3
5 x 5 + 2, 5 x 5 + 3
3) 결과
12, 13, 17, 18, 27, 28

(실습) 1부터 30까지의 숫자 중 소수를 찾아보자

1) 2를 제외한 2의 배수 제거
2) 3를 제외한 3의 배수 제거
3) 5를 제외한 5의 배수 제거
4) 7를 제외한 7의 배수 제거
5) 11을 제외한 11의 배수 제거
6) 13을 제외한 11의 배수 제거
7) 결과
2, 3, 5, 7, 11, 13, 17, 19, 23, 29

파이썬을 이용한 약수와 소수

• 파이썬을 이용해서 사용자가 입력한 숫자의 약수를 출력해보자

inputNumber = int(input('0보다 큰 정수 입력: '))

for number in range(1, (inputNumber + 1)):
    if inputNumber % number == 0:
        print('{}의 약수: {}'.format(inputNumber, number))

• 파이썬을 이용해서 사용자가 입력한 숫자까지의 소수를 출력해보자

inputNumber = int(input('0보다 큰 정수 입력: '))

for number in range(2, (inputNumber + 1)):
    flag = True
    for n in range(2, number):
        if number % n == 0:
            flag = False
            break

    if (flag):
        print('{} : 소수!!'.format(number))
    else:
        print('{} : 합성수!!'.format(number))

소인수

• 약소(인수) 중에서 소수인 숫자를 소인수라고 한다

소인수분해

• 1보다 큰 정수를 소인수의 곱으로 나타낸 것을 소인수분해라고 한다

소인수분해와 약수

• 소인수분해를 이용해서 약수를 정확하고 쉽게 구할 수 있다

파이썬을 이용한 소인수와 소인수분해

• 파이썬을 이용하여 사용자가 입력한 수를 소인수분해하자

inputNumber = int(input('1보다 큰 정수 입력: '))

n = 2
while n <= inputNumber:
    if inputNumber % n == 0:
        print('소인수: {}'.format(n))
        inputNumber /= n
    else:
        n += 1

• 72에 x를 곱하면 y의 제곱이 된다고 할때, x에 해당하는 가장 작은 정수를 구하자

inputNumber = int(input('1보다 큰 정수 입력: '))

n = 2
searchNumbers = []
while n <= inputNumber:
    if inputNumber % n == 0:
        print('소인수: {}'.format(n))
        if searchNumbers.count(n) == 0:
            searchNumbers.append(n)
        elif searchNumbers.count(n) == 1:
            searchNumbers.remove(n)
        inputNumber /= n
    else:
        n += 1

print('searchNumbers: {}'.format(searchNumbers))

공약수

• 두 개 이상의 수에서 공통된 약수를 공약수라고 한다

최대공약수

• 공약수 중 가장 큰 수를 최대 공약수라고 한다
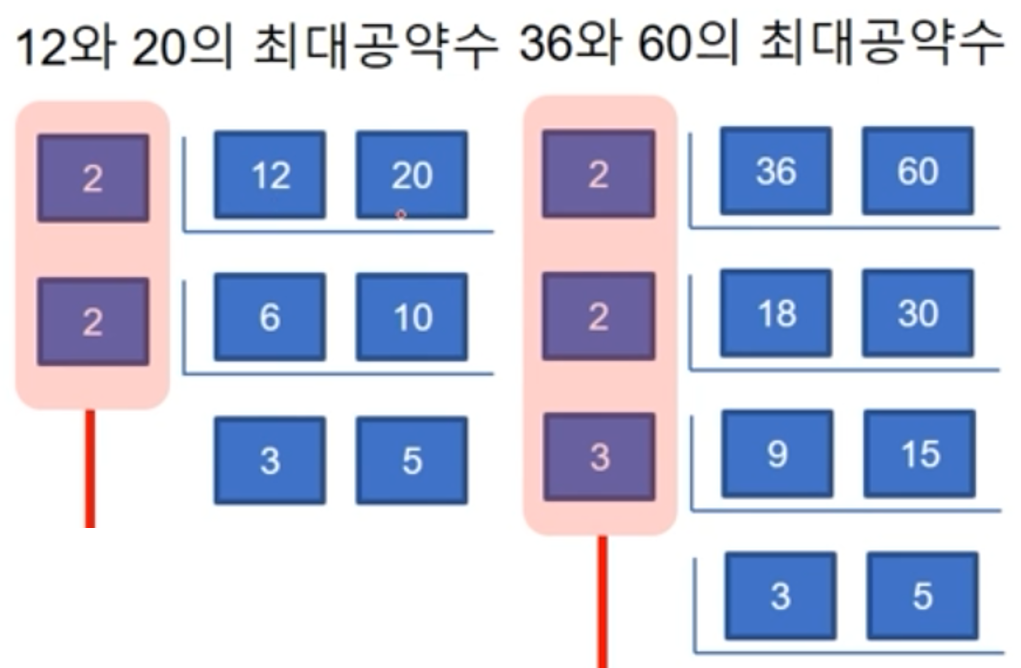
• 공통인 소인수의 거듭제곱에서 지수가 작은 수를 모두 곱한다
  ex) 12 = 2^2 x 3, 20 = 2^2 x 5 -> 최대공약수 : 2^2 = 4, 공약수 : 4의 약수 (1, 2, 4)
• 좀 더 편리하게 최대공약수 구하는 방법(소수로 나눗셈)
  

파이썬을 이용한 최대공약수

• 두 개의 수를 입력하면 공약수와 최대공약수를 출력하는 코드를 작성하자

num1 = int(input('1보다 큰 정수 입력: '))
num2 = int(input('1보다 큰 정수 입력: '))
maxNum = 0

for i in range(1, (num1 + 1)):
    if num1 % i == 0 and num2 % i == 0:
        print('공약수: {}'.format(i))
        maxNum = i

print('최대공약수: {}'.format(maxNum))

• 유클리드 호제법을 이용해서 최대공약수를 구할 수 있다(x, y의 최대공약수는 y, r(x%y)의 최대공약수와 같다.)
  

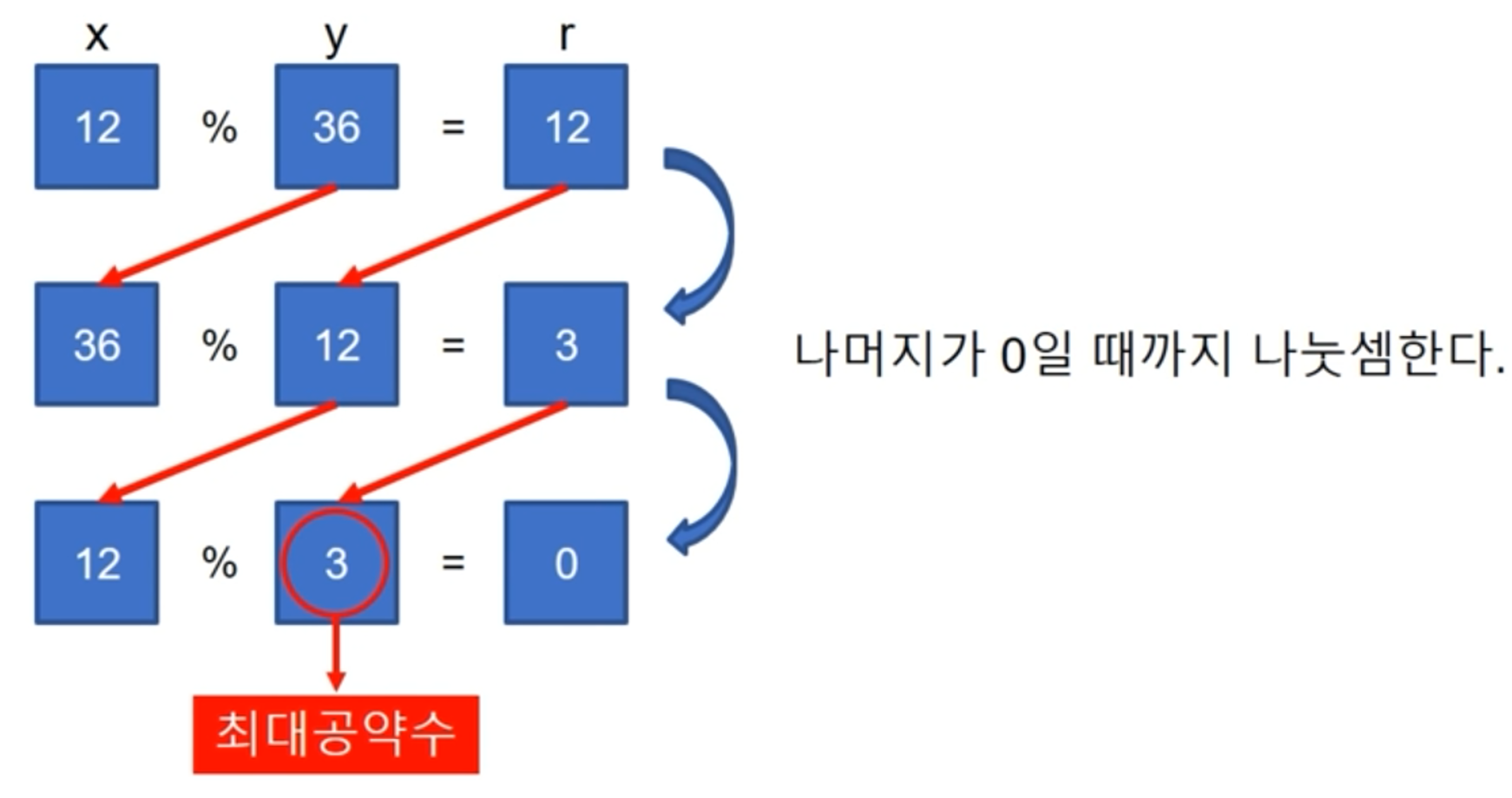
num1 = int(input('1보다 큰 정수 입력: '))
num2 = int(input('1보다 큰 정수 입력: '))

temp1 = num1; temp2 = num2

while temp2 > 0:
    temp = temp2
    temp2 = temp1 % temp2
    temp1 = temp

print('{}, {}의 최대공약수: {}'.format(num1, num2, temp1))

07 최소공배수 ~ 10 진법

공배수

• 두 개 이상의 수에서 공통된 배수를 공배수라고 한다

최소공배수

• 공배수 중 가장 작은 수를 최소공배수라고 한다

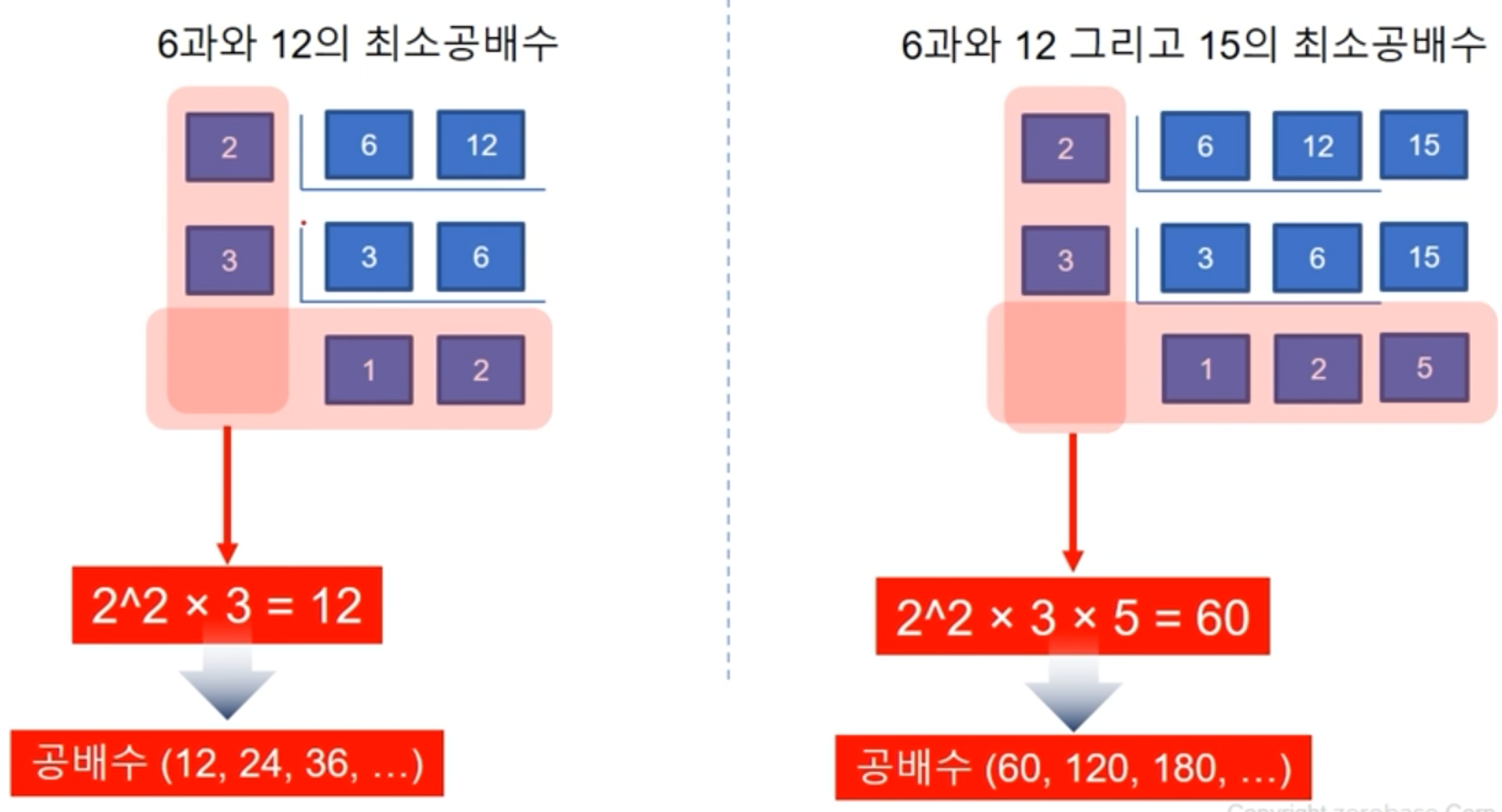
• 소인수분해를 이용하면 최소공배수 및 공배수를 구할 수 있다
  1) 공통인 소인수의 거듭제곱에서 지수가 크고 공통아닌 수를 모두 곱한다
  ex) 4 = 2^2 , 12 = 2^2 x 3 -> 2^2 x 3 = 12
  2) 공배수 = 최소 공배수의 배수
  ex) 12, 24, 36, ...

• 좀 더 편리하게 최소공배수 구하는
  방법
  

파이썬을 이용한 최소공배수

• 두 개의 수를 입력하면 최소공배수를 출력하는 코드를 작성하자

num1 = int(input('1보다 큰 정수 입력: '))
num2 = int(input('1보다 큰 정수 입력: '))
maxNum = 0

for i in range(1, (num1 + 1)):
    if num1 % i == 0 and num2 % i == 0:
        print('공약수: {}'.format(i))
        maxNum = i

print('최대공약수: {}'.format(maxNum))
minNum = (num1 * num2) // maxNum
print('최소공배수: {}'.format(minNum))

• 모든 배가 입항하는 날짜를 계산해 보자

ship1 = 3
ship2 = 4
ship3 = 5

maxDay = 0
for i in range(1, (ship1 + 1)):
    if ship1 % i == 0 and ship2 % i == 0:
        maxDay = i

print('최대공약수: {}'.format(maxDay))
minDay = (ship1 * ship2) // maxDay
print('{}, {}의 최소공배수: {}'.format(ship1, ship2, minDay))

newDay = minDay
for i in range(1, (newDay + 1)):
    if newDay % i == 0 and ship3 % i == 0:
        maxDay = i

print('최대공약수: {}'.format(maxDay))
minDay = (newDay * ship3) // maxDay
print('{}, {}, {}의 최소공배수: {}'.format(ship1, ship2, ship3, minDay))

진법

• 진법이란, 특정 숫자 몇 개를 사용하여 수를 표시하는 방법이다
  

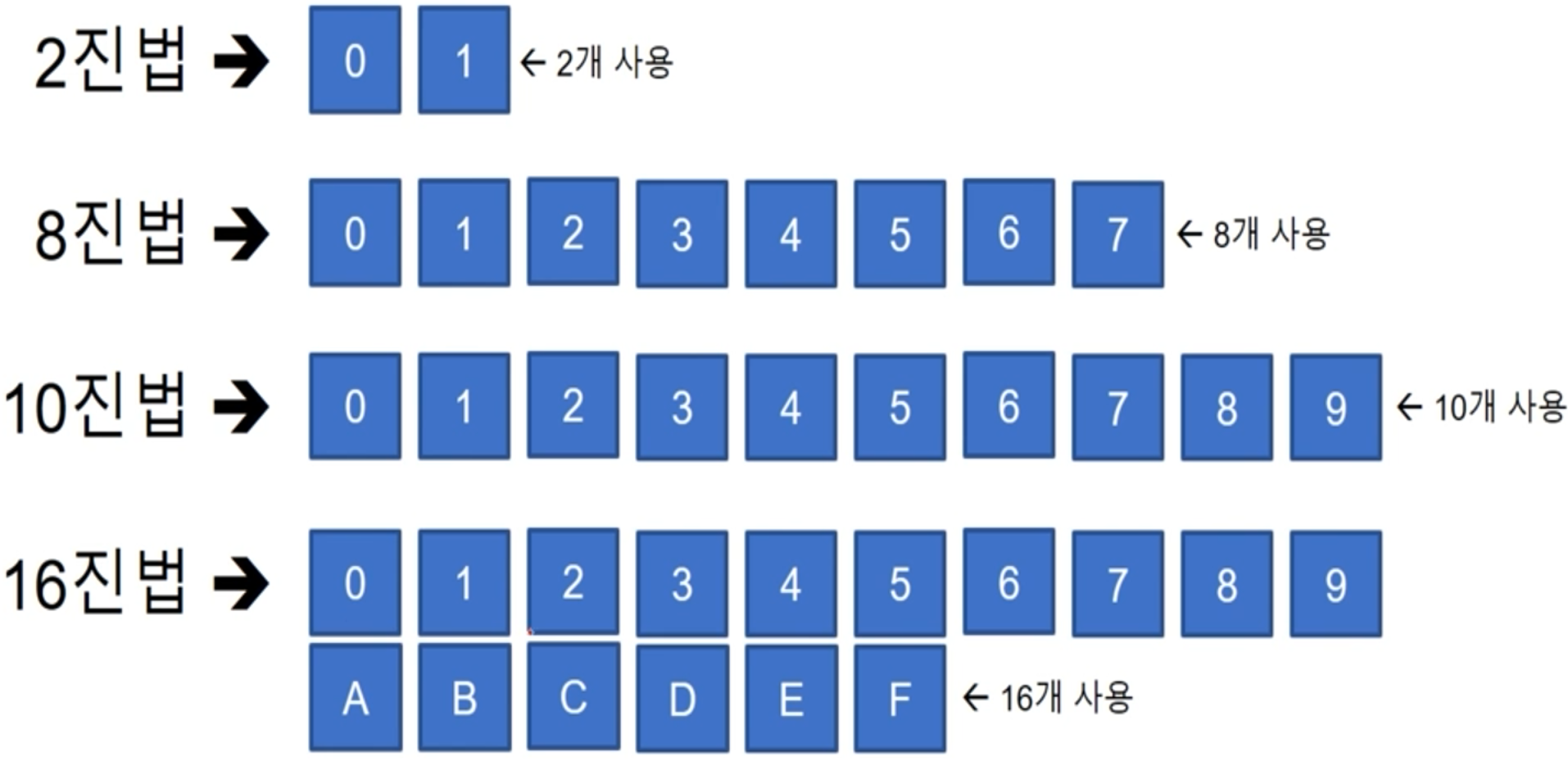
• 10진수 -> 2진수
  

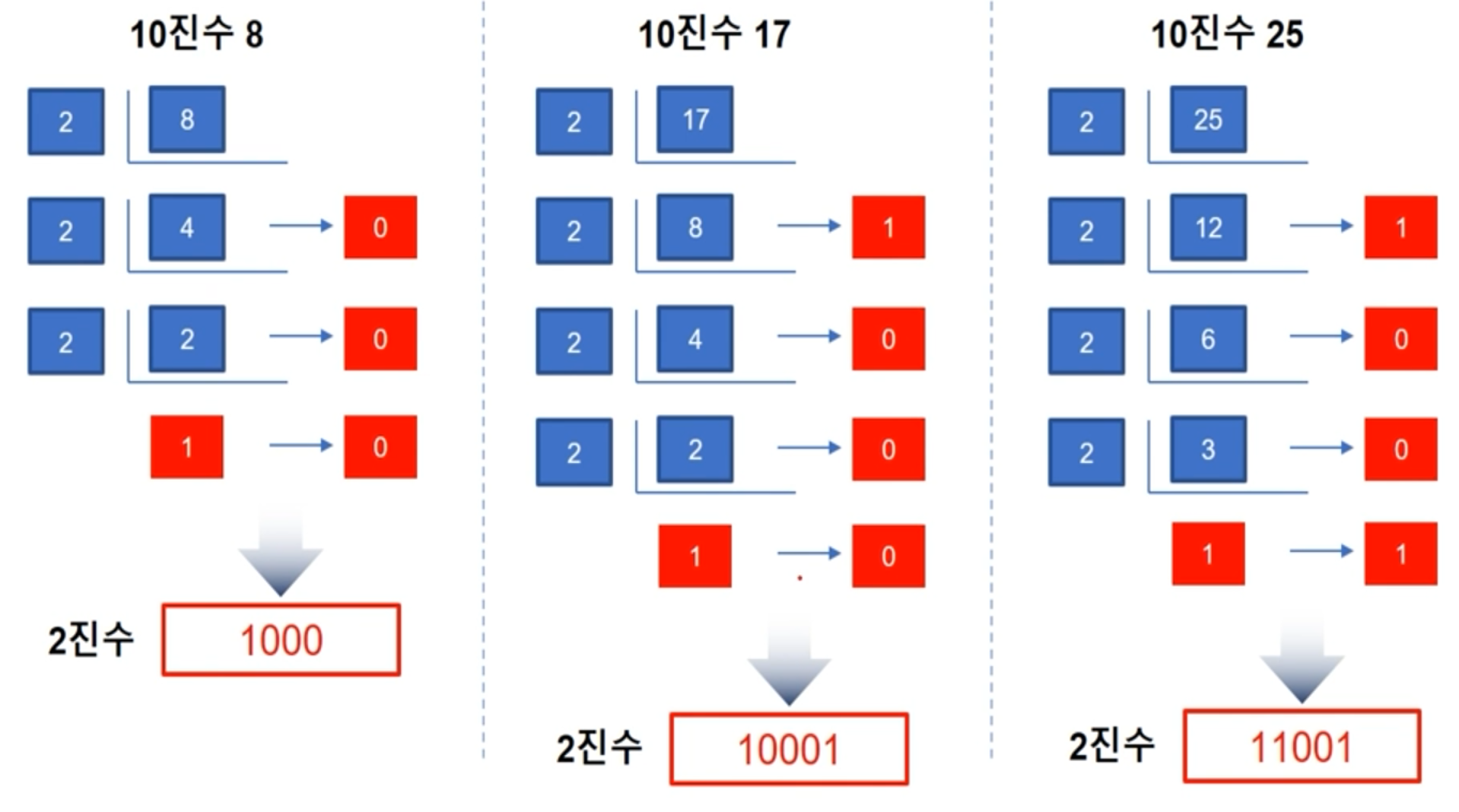
• 10진수 -> 8진수
  

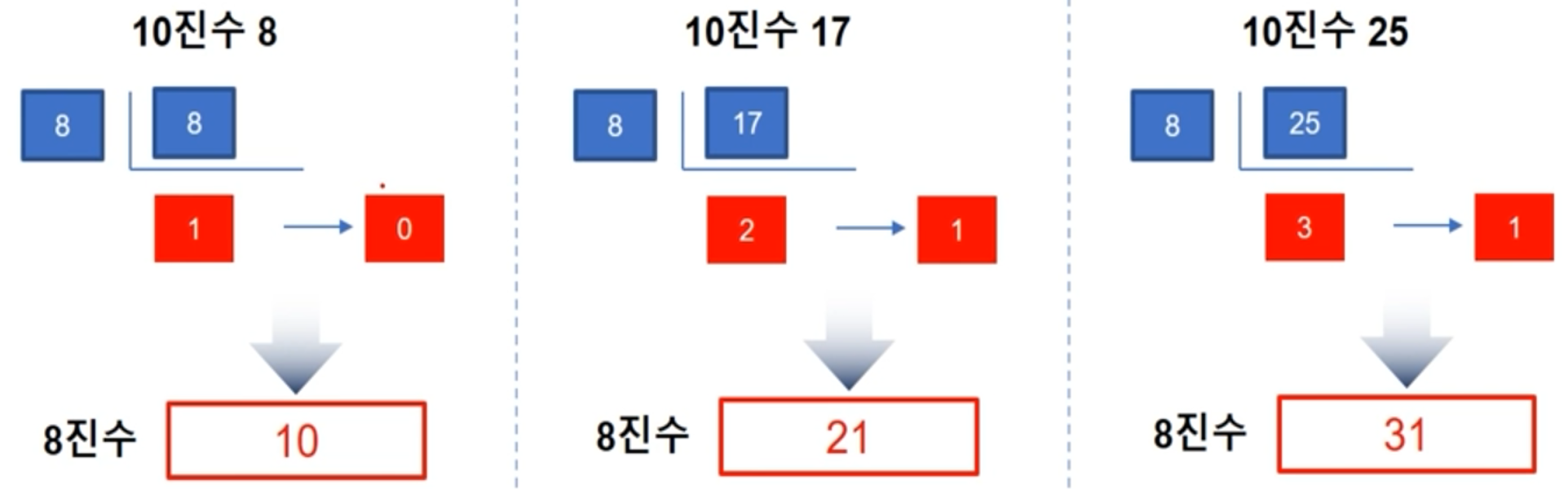
• 10진수 -> 16진수
  

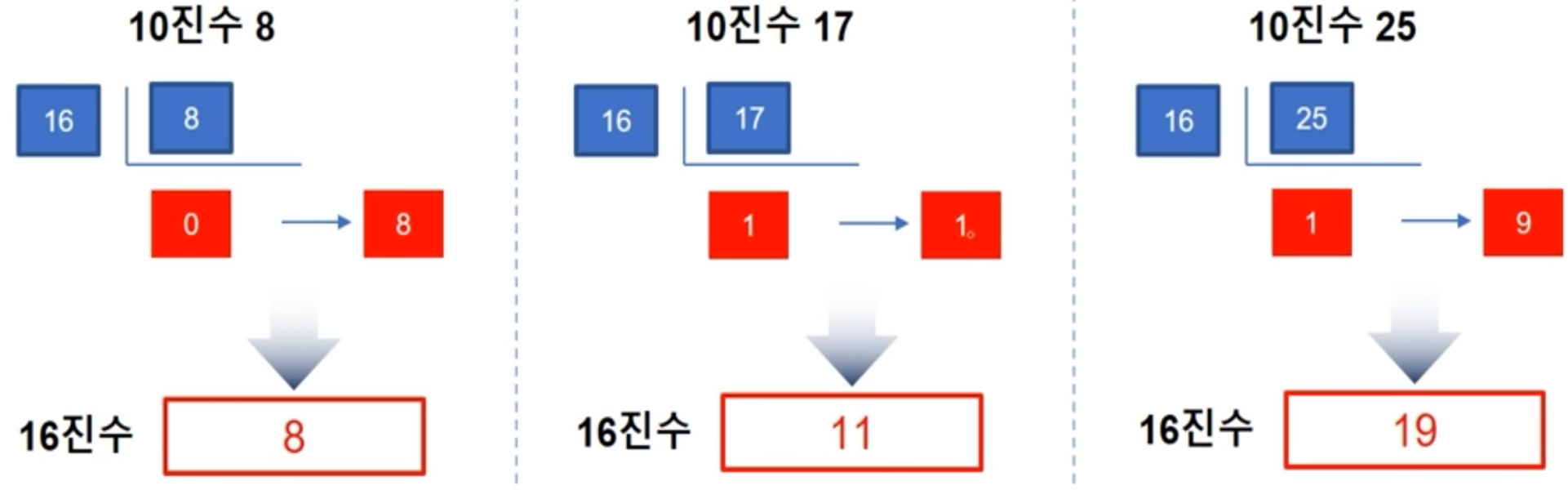
• 2진수 -> 10진수
  

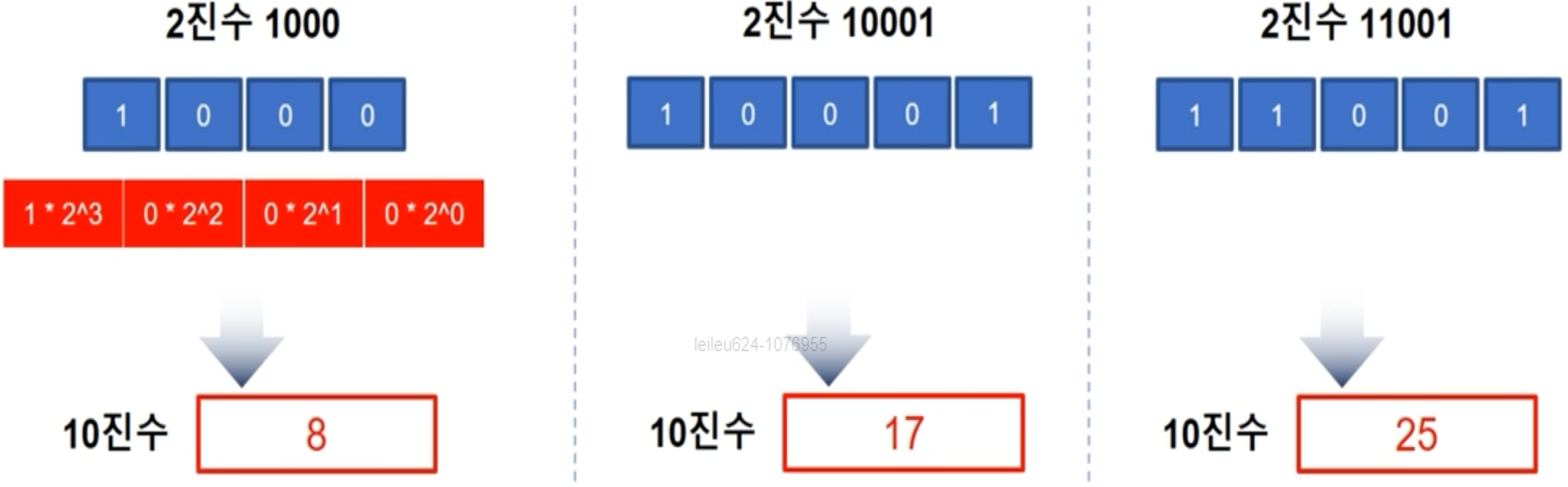
• 8진수 -> 10진수
  

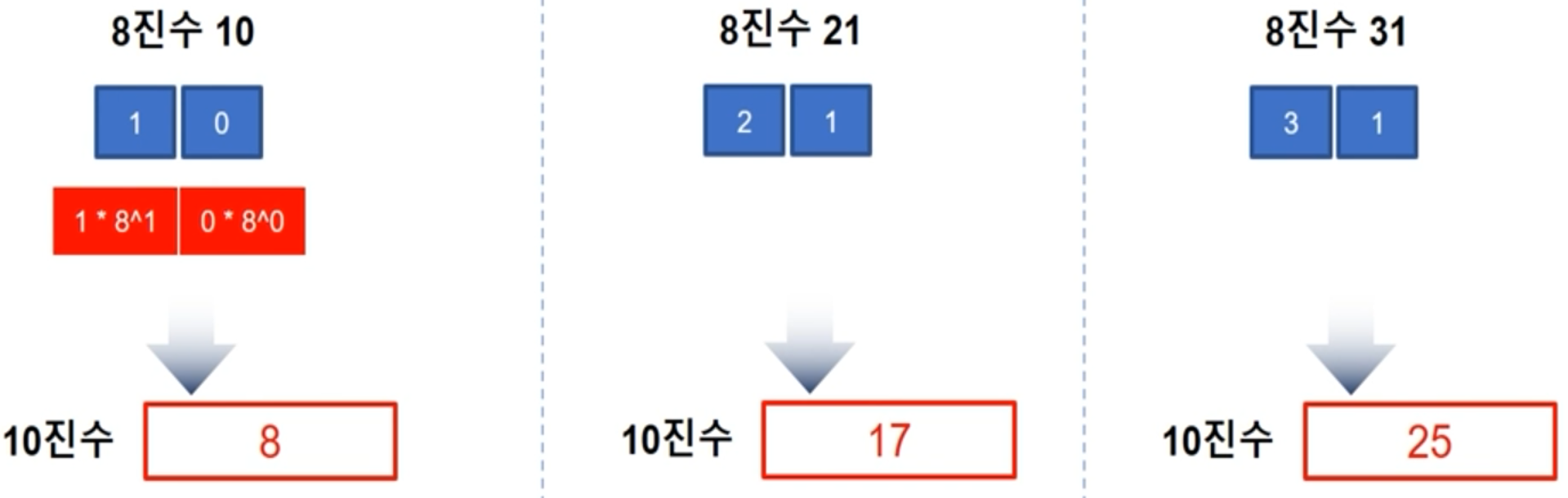
• 2진수 -> 8진수
  

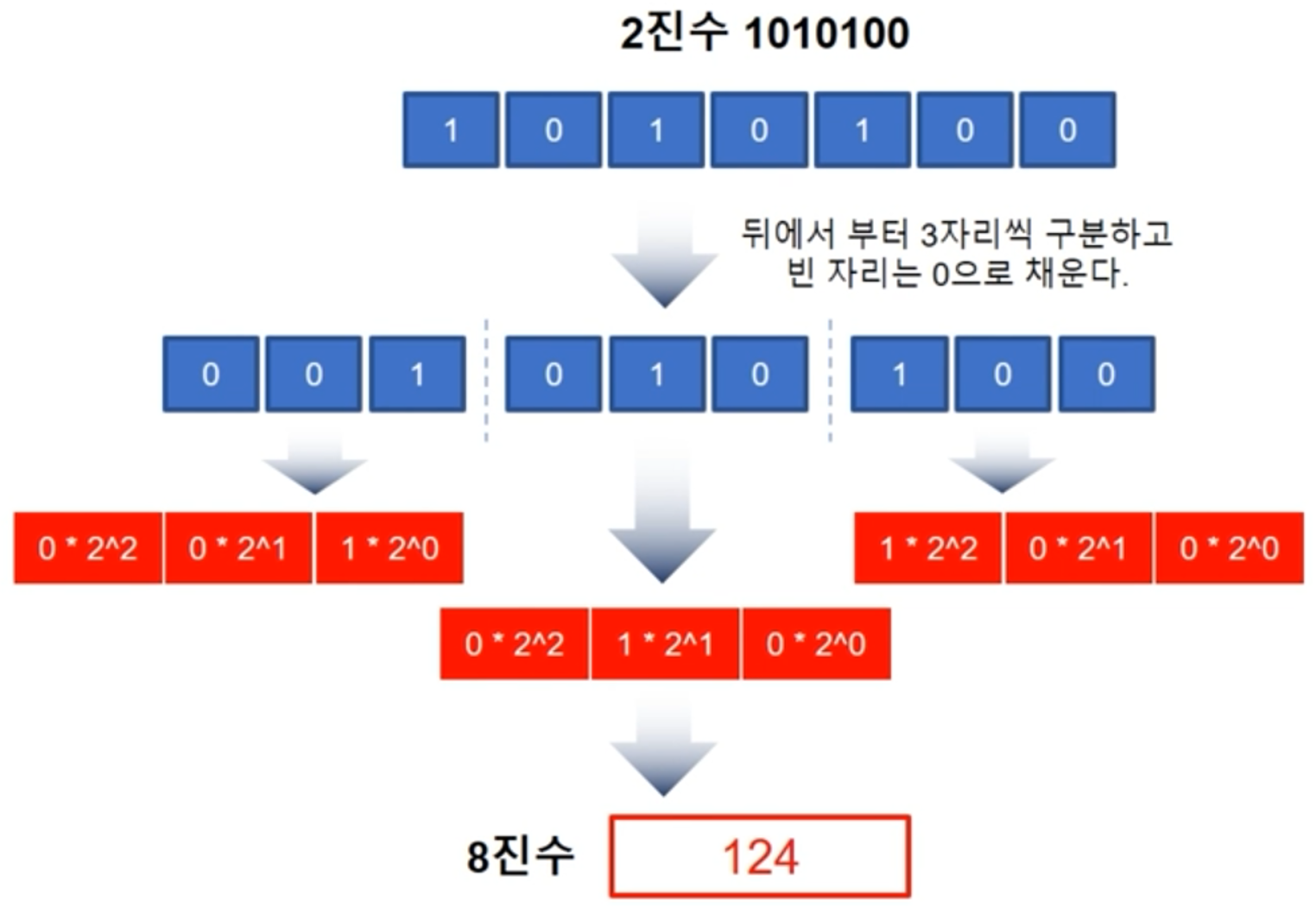
• 2진수 -> 16진수
  

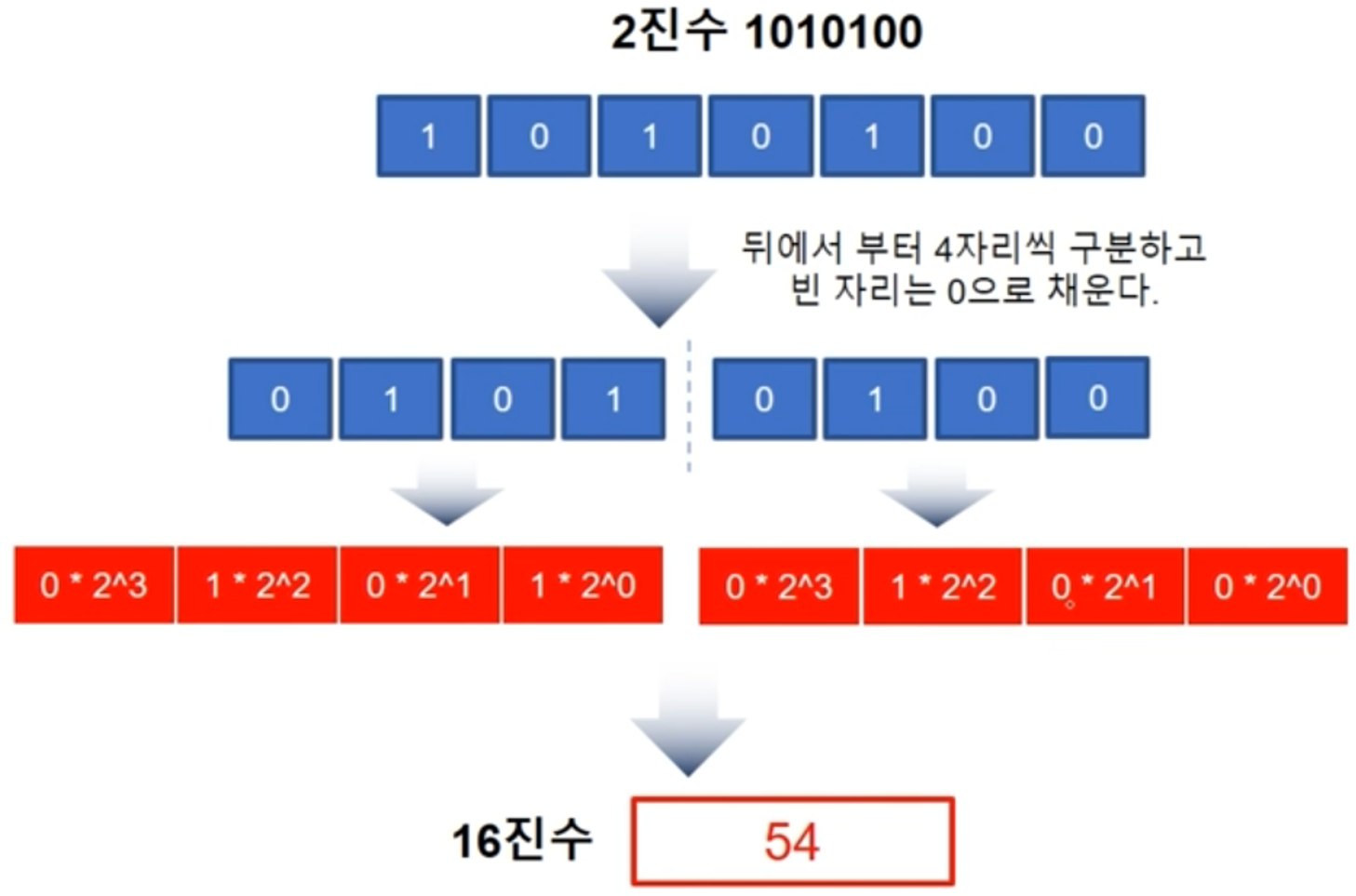
파이썬을 이용한 진법

• 10진수 -> 2진수, 8진수, 16진수
  

(변환 결과는 문자열)

dNum = 30

[10진수 -> X진수]

print('2진수: {}'.format(bin(dNum)))
print('8진수: {}'.format(oct(dNum)))
print('16진수: {}'.format(hex(dNum)))

[10진수 -> X진수(format()함수 이용)]

print('2진수: {}'.format(format(dNum, '#b')))
print('8진수: {}'.format(format(dNum, '#o')))
print('16진수: {}'.format(format(dNum, '#x')))
print('2진수: {0:#b}, 8진수: {0:#o}, 16진수: {0:#x}'.format(dNum))

• x진수 -> 10진수

print('2진수(0b11110) -> 10진수({})'.format(int('0b11110', 2)))
print('8진수(0o36) -> 10진수({})'.format(int('0o36', 8)))
print('16진수(0x1e) -> 10진수({})'.format(int('0x1e', 16)))

• x진수 -> x진수

print('2진수(0b11110) -> 8진수({})'.format(oct(0b11110)))
print('2진수(0b11110) -> 10진수({})'.format(int(0b11110)))
print('2진수(0b11110) -> 16진수({})'.format(hex(0b11110)))

print('8진수(0o36) -> 2진수({})'.format(bin(0o36)))
print('8진수(0o36) -> 10진수({})'.format(int(0o36)))
print('8진수(0o36) -> 16진수({})'.format(hex(0o36)))

print('16진수(0x1e) -> 2진수({})'.format(bin(0x1e)))
print('16진수(0x1e) -> 8진수({})'.format(oct(0x1e)))
print('16진수(0x1e) -> 10진수({})'.format(int(0x1e)))

11 수열 ~ 17 등비수열

수열

• 규칙성을 가지고 나열되어 있는 수들

항들의 합과 항의 관계

• 특정항은 특정항까지의 합에서 특정항 이전의 합까지의 합과 같다

등차 수열

• 연속된 두 항의 차이가 일정한 수열

등차 수열과 일반항

• 등차 수열 규칙성을 이용해서 일반항을 구할 수 있다

  

등차 중항

• 연속된 세 항에서 가운데 항

등차 수열의 합

• 규칙성을 이용해서 모든 항들의 총합을 구할 수 있다
  (첫항 + 마지막항) x (항의 개수) / 2

파이썬을 이용한 등차 수열

• 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자
  

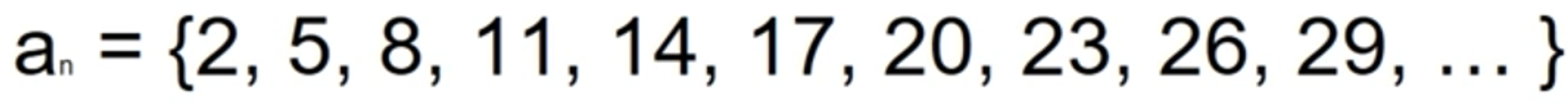
반복문 사용

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값: {}'.format(n, valueN))
        n += 1
        continue
    valueN += inputD
    print('{}번째 항의 값: {}'.format(n, valueN))
    n += 1
print('{}번째 항의 값: {}'.format(inputN, valueN))

등차 수열(일반항) 공식: an = a1 + (n-1) * d

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0

valueN = inputN1 + (inputN-1) * inputD
print('{}번째 항의 값: {}'.format(inputN, valueN))

• 다음 수열을 보고 n번째 항까지의 합을 출력하는 프로그램을 만들어보자
  

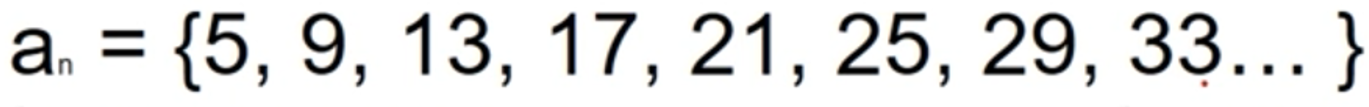
반복문 사용

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        sumN += valueN
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    valueN += inputD
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1
print('{}번째 항까지의 합: {}'.format(inputN, sumN))

등차 수열(합) 공식: sn = n(a1 + an) / 2

inputN1 = int(input('a1 입력: '))
inputD = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1

valueN = inputN1 + (inputN-1) * inputD
sumN = inputN * (inputN1 + valueN) / 2
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))

등비 수열

• 연속된 두 항의 비가 일정한 수열

등비 수열과 일반항

• 등비 수열 규칙성을 이용해서 일반항을 구할 수 있다

  

등비 중항

• 연속된 세 항에서 가운데 항

등비 수열의 합

• 규칙성을 이용해서 모든 항들의 총합을 구할 수 있다

  

파이썬을 이용한 등비 수열

• 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자
  

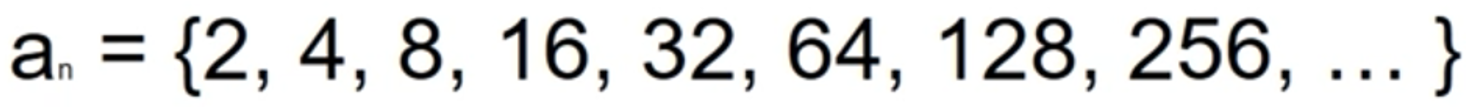
반복문 사용

inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        print('{}번째 항의 값: {}'.format(n, valueN))
        n += 1
        continue
    valueN *= inputR
    print('{}번째 항의 값: {}'.format(n, valueN))
    n += 1
print('{}번째 항의 값: {}'.format(inputN, valueN))

등비 수열(일반항) 공식: an = a1 * r^(n-1)

inputN1 = int(input('a1 입력: '))
inputR = int(input('공차 입력: '))
inputN = int(input('n 입력: '))

valueN = 0

valueN = inputN1 * (inputR ** (inputN-1))
print('{}번째 항의 값: {}'.format(inputN, valueN))

• 다음 수열을 보고 n번째 항까지의 합을 출력하는 프로그램을 만들어보자
  

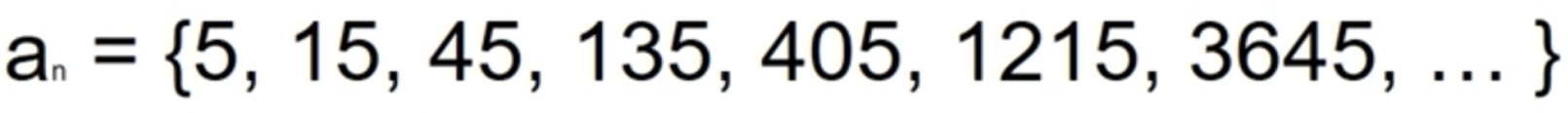
반복문 사용

inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1

while n <= inputN:
    if n == 1:
        valueN = inputN1
        sumN += valueN
        print('{}번째 항까지의 합: {}'.format(n, sumN))
        n += 1
        continue
    valueN *= inputR
    sumN += valueN
    print('{}번째 항까지의 합: {}'.format(n, sumN))
    n += 1
print('{}번째 항까지의 합: {}'.format(inputN, sumN))

등비 수열(합) 공식: sn = a1 * (1 - r^n) / (1-r)

inputN1 = int(input('a1 입력: '))
inputR = int(input('공비 입력: '))
inputN = int(input('n 입력: '))

valueN = 0
sumN = 0
n = 1

sumN = inputN1 * (1 - (inputR ** inputN)) / (1 - inputR)
print('{}번째 항까지의 합: {}'.format(inputN, int(sumN)))

18 시그마 ~ 20 계차 수열

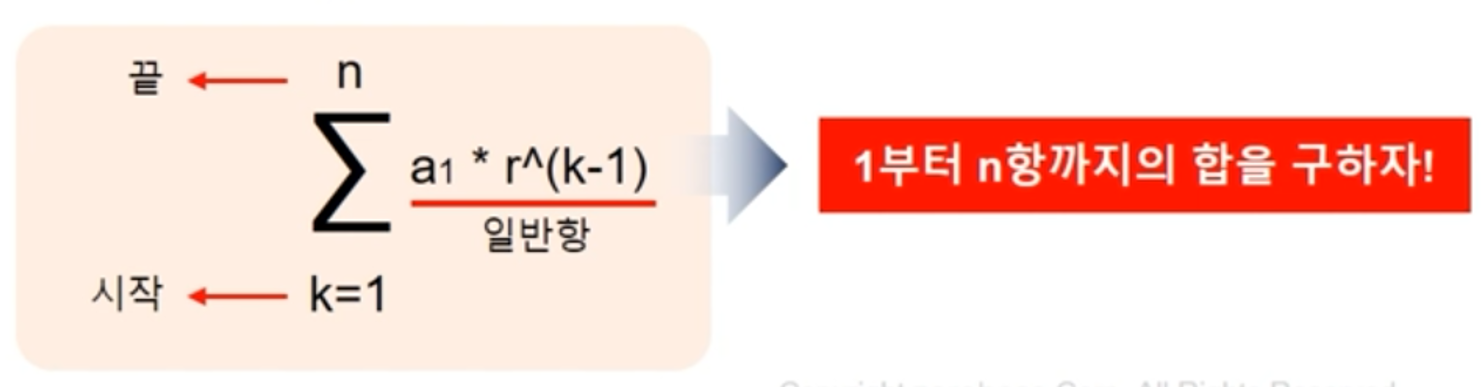
시그마

• Σ란 수열의 합을 나타내는 기호이다
  

계차 수열

• 어떤 수열의 인접하는 두 항의 차로 이루어진 또 다른 수열
  

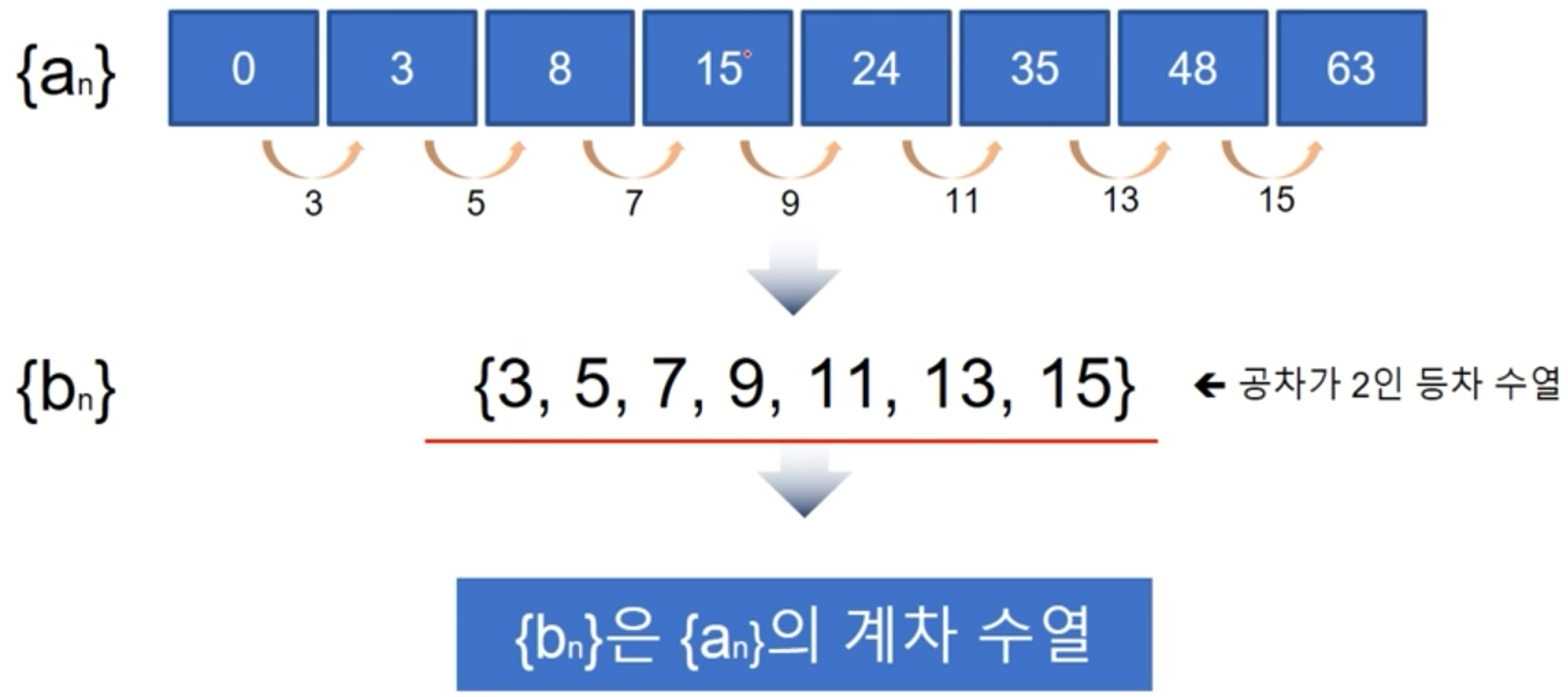
계차 수열과 일반항

• 계차 수열을 이용해서 수열 an의 일반항을 구할 수 있다
  

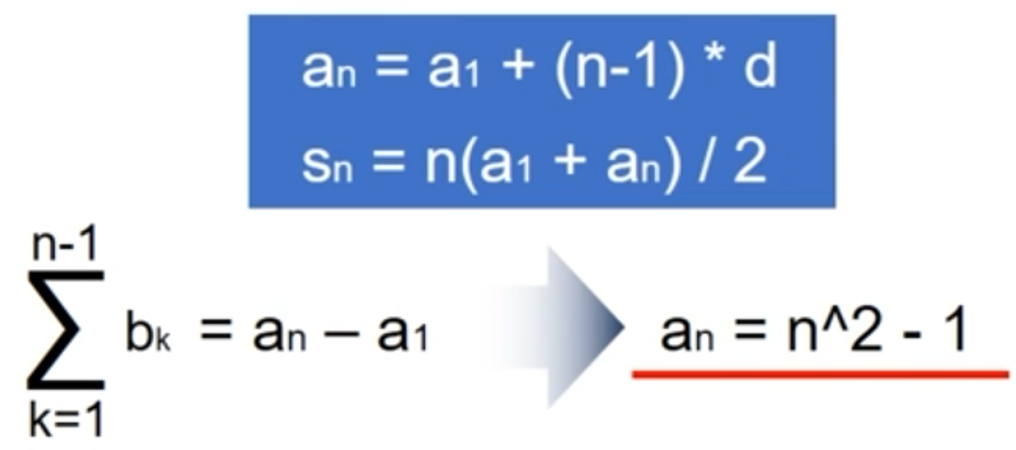
파이썬을 이용한 계차 수열

• 다음 수열을 보고 n번째 항의 값을 출력하는 프로그램을 만들어보자
  

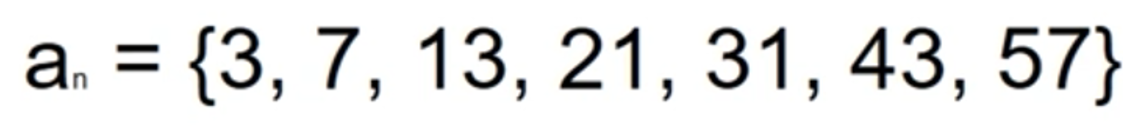
 an = {3, 7, 13, 21, 31, 43, 57}
        4   6   8   10  12  14

반복문 사용

inputAN1 = int(input('a1 입력: '))
inputAN = int(input('an 입력: '))
inputBN1 = int(input('b1 입력: '))
inputBD = int(input('bn 공차 입력: '))

valueAN = 0
valueBN = 0
n = 1

while n <= inputAN:
    if n == 1:
        valueAN = inputAN1
        valueBN = inputBN1
        print('an의 {}번째 항의 값: {}'.format(n, valueAN))
        print('bn의 {}번째 항의 값: {}'.format(n, valueBN))
        n += 1
        continue
    valueAN += valueBN
    valueBN += inputBD
    print('an의 {}번째 항의 값: {}'.format(n, valueAN))
    print('bn의 {}번째 항의 값: {}'.format(n, valueBN))
    n += 1
print('an의 {}번째 항의 값: {}'.format(inputAN, valueAN))
print('bn의 {}번째 항의 값: {}'.format(inputAN, valueBN))

n^2 + n + 1 = an

inputAN1 = int(input('a1 입력: '))
inputAN = int(input('an 입력: '))

valueAN = inputAN ** 2 + inputAN + 1
print('an의 {}번째 항의 값: {}'.format(inputAN, valueAN))

총평

재미있었던 부분

오랜만에 중고등학교때 배웠던 수학들을 보니 기억이 새록새록 다시 나면서 파이썬에 대입해 수학을 배우니 훨씬 기억에도 잘 남았고 재미있었다

어려웠던 부분

복습으로 한 파이썬 중급 문제풀이 마무리 부분은 진짜 지옥이었다
너무 어려웠고 역시나 한번보고 이해가는 문제는 손에 꼽을정도였다

느낀점 및 내일 학습 계획

파이썬 중급 문제풀이 부분은 계속 다른 공부 하면서 병행을 하던지, 다시 되돌아가서 여러번 공부해야겠다
그렇지 않고서는 머리에 잘 안남겠다고 확신했다 ㅋㅋ.. 내일은 기초 수학 다음부분을 공부 할 예정이다