📐 막간 - 미분
✅ 고전역학의 대부분은 시간의 연속적인 변화에 따라 나타나는 연속적인 변화를 다룬다. 따라서 우리는 연속적인 변화에 수학적으로 대처하기 위해 미적분이라는 수학을 사용한다.
극한의 개념과 도함수
극한
-
어떤 수열이 증가함에 따라 어떤 값 에 점점 더 가까이 다가가면, 이 수열의 극한은 이다.
→ 그 어떤 항도 과 같지는 않지만, 점점 더 에 가까워진다. -
매개변수 에 따라 그 값이 변하는 함수 에 대해서 만약 가 에 가까워질 수록 가 어떤 값 에 점점 더 가까이 다가가면, 가 에 다가갈 때의 의 극한이 이다.
⇒ 는 가 변함에 따라서 그 함숫값이 함께 변화한다. 미분법은 이러한 함수의 변화율을 다룬다.
도함수
-
변화율 : 의 변화에 대한 의 변화의 비율
-
가 어떤 시간 만큼 변화하면, 이 시간동안 함수 는
-
이때 이 시간간격 를 아주 작게, 0에 가까이 극한을 보냈을 때 변화율의 극한값을 정의할 수 있다.
- , 모두 0으로 수렴하지만, 이들의 비율은 어떤 극한값으로 나타난다.
- 이를 에 대한 의 도함수라고 한다.
-
위 과정을 거쳐서 다양한 함수의 도함수를 계산할 수 있다.
🎾 입자의 운동
입자?
점 입자는 이상적인 개념이다.
- 현실세계에서 그 어떤 물체도 ‘점’이라고 할 만큼 작지 않다.
- 하지만 물리학에서 상대적으로 작은 것들을 점으로 간주하고는 한다.
ex) 태양 주위를 공전하는 지구에 대한 궤도를 계산할 때, 지구의 크기를 무시
입자의 위치
위치의 표현
- 입자의 위치는 3개의 공간 좌표값을 부여하여 정해진다.
- 에 대한 3개의 축에 대한 함수
- 벡터 표현법
- 각 성분을 로 가지는 벡터
- 이때, 입자의 경로는 로부터 정해진다.
입자의 속도
속도의 정의
- 가 어떤 시간 만큼 변화하면, 이 시간동안 시간에 따른 함수인 or 는 변화한다.
- 순간적인 속도 - 시간에 따른 위치의 변화율
*물리량의 표현
-
뉴턴 표기법 : 어떤 양 위에 위치된 점()은 시간 도함수를 취한다는 약속된 표기법
ex) -
압축된 표기법
- 3개의 위치에 대한 좌표
- 속도 성분
- 3개의 위치에 대한 좌표
속력
- 속도 벡터의 크기
- 방향과 상관없이 입자가 얼마나 빨리 움직이는지를 나타낸다.
입자의 가속도
가속도의 정의
- 시간에 따른 속도의 변화율
- 속도의 도함수
- 위치에 대한 2차 시간 도함수
(뉴턴표기법)
🪂 운동의 예
자유낙하 운동
축을 따라 중력가속도()만큼 가속되는 낙하하는 입자의 운동 (다른 두 방향으로는 운동이 없다)
위치의 방정식
- 방향으로는 움직이지 않음 (정지상태)
- 축을 따라서 움직인다.
속도의 방정식
속도 : 시간에 따른 위치의 변화율
- 성분은 항상 0
- 성분의 속도의 방정식은 초기 속도 로 구성되는데, 시간이 에서 증가함에 따라 결국 상수인 은 gt항에 따라잡히게 되어 운동방향은 방향으로 변화한다.
가속도의 방정식
가속도 : 시간에 따른 속도의 변화율
- 성분은 항상 0
- 축방향의 가속도는 음수인 상수로 이다.
⇒ 위에서 설명한 방정식에서 만약 축이 높이를 나타낸다면, 이 운동은 일정 높이 ()에서 낙하하는 물체와 동일한 방식으로 운동하게 될 것이다.
단순 조화 운동
x축을 따라 앞뒤로 움직이며 진동하는 입자의 운동 (다른 두 방향으로는 운동이 없다)
단순한 진동운동의 방정식 표현에는 삼각함수를 이용한다.
위치의 방정식
는 상수로, 이 값이 클수록 입자는 더 급속으로 진동한다. (주기가 짧다)
그래프
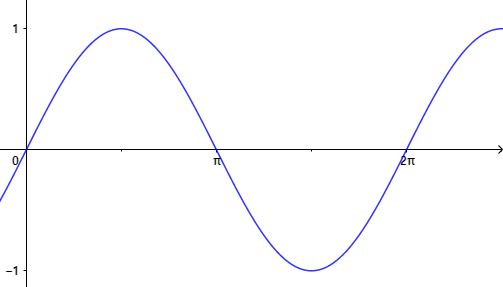
속도와 가속도의 방정식
-
위치와 속도의 위상차는 이다.
위치 가 최댓값이나 최솟값을 가질 떄, 그 속도는 0
↔ 위치가 0일 떄 그 속도는 최대이거나 최소 -
위치와 가속도의 위상차는 이다.
- 가속도의 방정식과 위치의 방정식 모두 에 비례하지만, 가속도는 위치와 반대방향으로 작용한다.
- 가 양수이면 는 음수, 가 음수이면 는 양수이다.
- 입자가 어디에 위치하든간에, 원점 방향으로 되돌아가게 가속도가 작용한다.
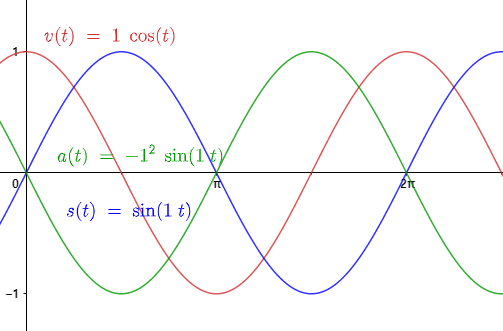
, 두 그래프는 만큼 축상의 차이가 존재
두 그래프는 만큼 축상의 차이가 존재
+값에 따른 그래프 변화
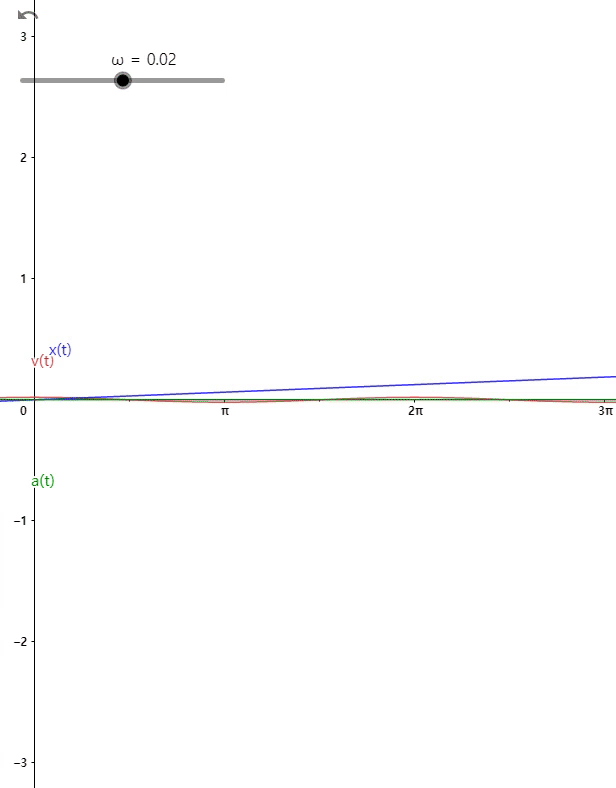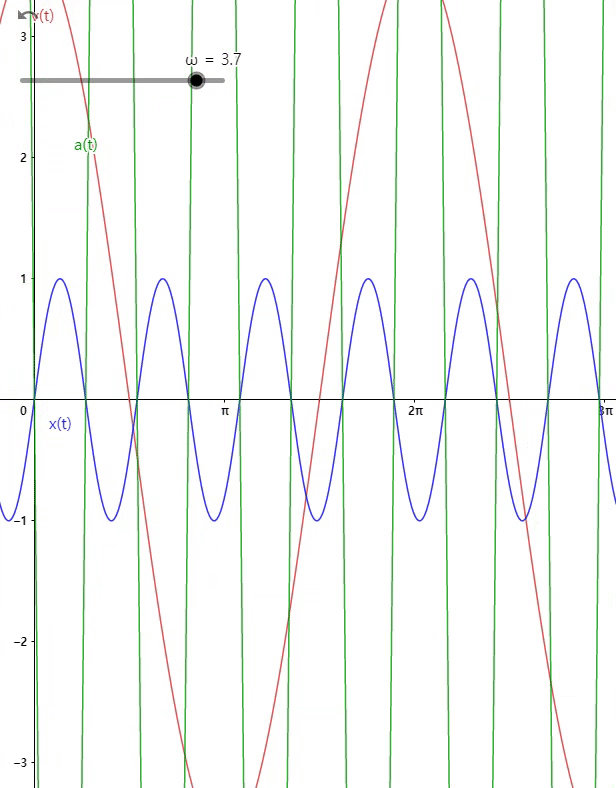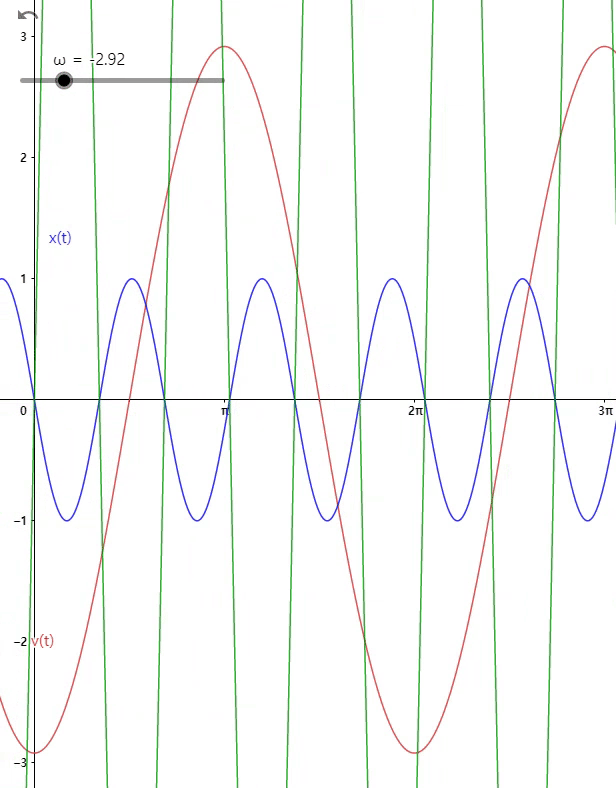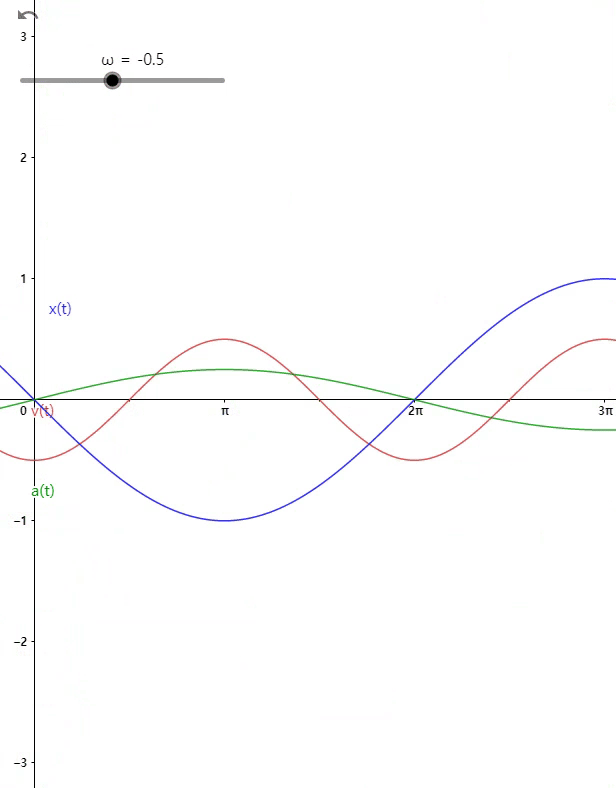
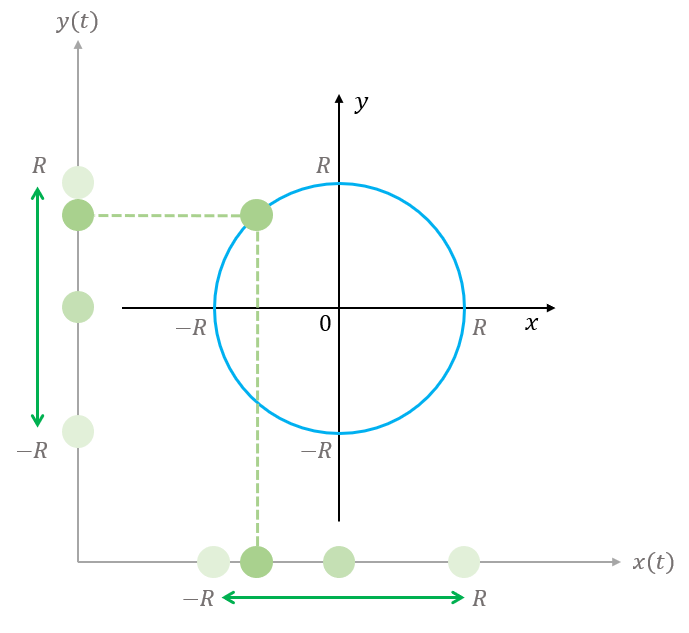
원운동
평면에서 원점을 중심으로 일정한 속력으로 원을 따라 움직이는 입자의 운동 (축 방향은 무시)
평면상의 운동을 표현하기 위해, 에 대한 위치의 함수 와 가 있어야 한다.
단순 조화운동으로 생각한 원운동 - 위치의 방정식
축 축에 대해 각각 위상차가 도인 단순 조화운동을 하는 입자의 운동
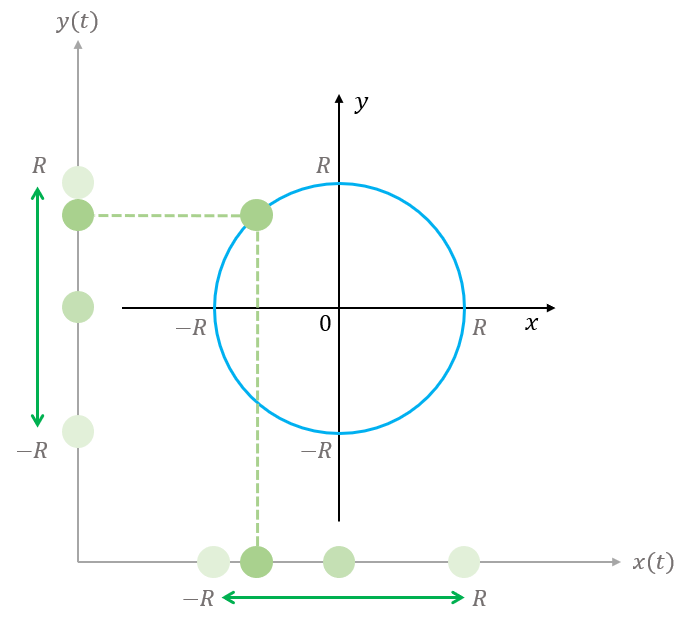
축, 축에 투영한 원운동의 그림
- 궤도 반지름을 이라고 할 때, 평면상에서 일어나는 원운동을 각각의 축에 투영시켜 생각하자.
- 입자는 축 상에서 과 사이를 진동하고, 축에서 또한 과 사이를 진동한다.
- 단 축상에서의 좌표와 축 상에서의 좌표에는 의 위상차가 나타난다.
- 가 최대()이면 는
- 가 최대()이면 는
각진동수
- 는 각진동수로, 단위시간당 각이 진행한 라디안으로 정의된다.
- 주기 와 관련있다.
속도, 가속도의 방정식
-
원운동에서 가속도벡터는 위치벡터와 평행하지만 그 방향은 반대이다.
→ 가속도벡터는 원점을 향해 안쪽으로 작용한다.
-
위치벡터와 속도벡터는 수직이다.
공식 정리


📐 막간. 적분법
⚡ 미분법은 변화율과 관계가 있고 적분법은 수많은 미세한 증가량들의 합과 관계있다. → 둘은 분명 관계가 있다.
정적분의 정의
적분법의 핵심적인 문제는 어떤 함수의 곡선 아래의 넓이를 계산하는 것이다.
-
특정 구간을 적분하기 위해 임의의 두 값 a와 b를 생각한다. [적분한계]
-
해당 구간에서 가지는 넓이의 영억을 여러개의 동일한 가로길이를 가지는 직사각형들로 쪼개서 생각한다.
-
이러한 직사각형들을 모두 더한 값은, 그래프 아래의 영역과 어느정도 비슷-근사- 하다고 볼 수 있다.
⇒ 만약 각각의 직사각형의 폭을 0으로 아주 작게 줄여 선으로 생각할 수 있다면, 이는 해당 영역의 넓이와 같다고 생각할 수 있다.
한도 와 사이의 함수의 정적분은 그렇게 정의된다.
(적분기호가 시그마를 대체하고, 는 로 대체된다.)
부정적분과 미적분학의 기본정리
부정적분
- 정적분에서 적분 한도 둘 중 하나를 정해진 값인 상수가 아니라, 변수로 생각한 것
- 고정된 값에서 변수까지 적분한 것
- 주로 적분한계없이 표현한다
미적분학의 기본정리
fundamental therem of calculus
수학에서 가장 단순하면서도 가장 아름다운 결과
- 적분과 미분 사이에 깊은관계가 존재함을 보이는 정리
과정 설명
- 부정적분을 정의할 때 사용했던 변수 에서 아주 작은 증가분 만큼이 더해진 에 대한 부정적분을 생각해보자.
- 이는 폭이 인 직사각형을 1개 더 추가한 셈이기 때문에, 에 대한 부정적분과 에 대한 부정적분의 차이는 추가된 직사각형 넓이인 와 같다.
- 위 성질을 이용하여 수식으로 표현한 것을 도함수의 기본정의 꼴 (로 나누고 인 극한을 취함)로 표현하면, 미적분과 적분을 연결하는 기본 정리를 찾아낼 수 있다.
적분과 미분의 과정은 역관계이다.
- 이는 어떤 함수의 도함수로부터 기존함수을 얻어낼 수 있다는 의미이다. → 이를 이용하여 여러 함수의 부정적분을 구할 수 있다.
- 부정적분의 결과에 추가되는 상수 C는 두 적분한계가 동일한 경우 그 적분값이 0이 된다는 사실을 이용해서 구할 수 있다.
미적분학의 기본정리
적분 방법
부분적분
🌊 만약 혼자서 알지 못하는 적분을 해결하고자 하려면, 교과서에 나오는 가장 오래된 해결법은 부분적분이다.
(곱의 미분을 적분으로 표현한 것)
공식 정리

본 포스팅은 레너드 서스킨드의 물리의 정석 - 고전 역학편을 기반으로 작성되었습니다.