1장. 고전 물리학의 본성

🚀 고전 물리학에서는 이론상으로,
현재 계의 상태와 상태를 변화하는지를 결정짓는 방정식을 알고있다면 미래를 예측할 수 있다.

⚡고전 물리학이란?

고전 물리학의 종류 - 입자에 대한 뉴턴의 운동방정식
- 전자기장에 대한 맥스웰 - 페러데이 이론
- 아인슈타인의 일반 상대성 이론
기타...

계와 상태 공간

계(system)

• 계 : 입자, 장(field), 파동 등 개체들의 집합
• 닫힌계 : 외부로 부터 고립된 계
• 고전역학에서 계의 특성 : 도약이나 중단 없이 연속적인 성질을 가진다. (↔ 양자역학에서 빈번히 일어나는 불연속적인 과정과 반대)

상태공간

• 어떤 계가 차지하는 모든 상태들의 집합
• 각각의 상태에 이름을 붙여서 이들을 원소로 가지는 수학적인 의미의 집합과 같다.
• 예시 : 앞 뒷면을 가지는 동전의 계
  • 계는 앞면과 뒷면인 2개의 상태를 가진다.
  • 앞면과 뒷면 각각에 이름을 붙여$(F, B)$ 이를 원소로 갖는 집합을 생각할 수 있다.
  • 상태공간 집합 : $\{ F, B \}$

동역학적 계

• 시간에 따라 변화하는 계
• 운동법칙(동역학 법칙)을 수반한다.

동역학 법칙

동역학 법칙 : 현재 상태가 주어지면, 그 다음 상태를 말해주는 규칙

동역학 법칙의 방정식 표현

• 자유도 : 어떤 계를 방정식의 형태로 기술하는 변수 $σ$
• 연속적인 시간의 흐름은 $t$ 로 기호화 (변화가 불연속일 때는 n을 사용 )
  ⇒ 시간 t에서의 상태 : $σ(t)$
• ex) 2개의 상태 $(σ=1,-1)$ 를 갖는 불연속적인 계에서 동역학 법칙의 방정식 표현
  • 그 다음 상태가 이전상태와 동일할 때 ($-1 → -1$ or $1 → 1$)
    $\sigma(n+1) = \sigma(n)$
  • 그 다음 상태가 다른 상태일 때 ($-1 → 1$ or $1 → -1$)
    $\sigma(n+1) = -\sigma(n)$

동역학 법칙의 종류

• 순환적 : 각 상태가 끊임없이 반복되는 패턴
• 독립적인 순환 패턴 여러개로 구성
  ⇒ 이때 하나의 순환에서 다른 순환으로 뛰어넘는 것을 동역학 법칙이 허용하지 않기 때문에, 순환은 보존된다.
  

동역학 법칙의 조건

1. 결정론적이다.  
2. 가역적이다.

결정론적

✅ 모든 미래의 상태는 그 이전의 상태에 따라서 결정되기 때문에, 고전역학은 미래가 정해져있다.
⇒ 따라서 고전역학의 모든 기본 법칙들은 결정론적이다.

• 순환적 : 상태가 변화하는 과정이 끊임없이 반복됨
• 독립적인 여러 패턴 : 어떤 패턴이 이루는 원소 중 하나의 상태에서 시작된다면 결코 다른 패턴이 가지는 원소에 이를 수 없다. → 다른 쪽으로 갈 수 없다.

가역적

• 법칙에 따라 변화하는 상태의 화살표를 반대로 뒤집었을 때도 결정론적이다.
• 동역학 법칙이 미래뿐만아니라 과거를 기준으로 했을 때도 결정론적이어야 한다.
• 비가역적인 계의 화살표를 반대로 뒤집은 계는, 미래로서 비결정론적인 계가 된다.

정보의 보존

결정론적이고 가역적임을 나타내는 법칙

1. 어디로 가야할지를 알려주는 유일한 하나의 화살표가 존재 (출발)
2. 어디에서 왔는지를 알려주는 유일한 하나의 화살표가 존재 (도착)

• 정보의 보존

  특정한 어떤 법칙; 동역학적 법칙에 의해 현재 상태에서 다른 상태로 변화할 수는 있지만, 결국 무수히 많은 상태를 가진 계를 거친 뒤에는 다시 원래 상태로 되돌아오게 된다. [순환]

불연속 계의 예시

다음과 같이 6개의 상태를 가진 불연속적인 계를 생각해보자.

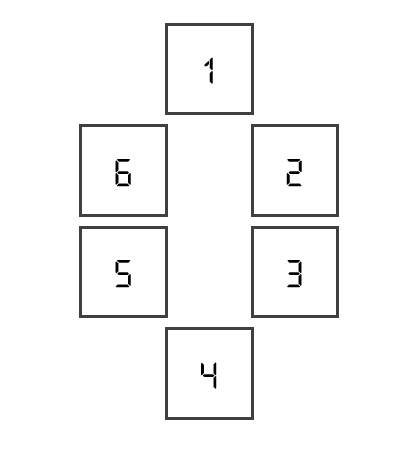
• 생각할 수 있는 다양한 동역학 법칙 패턴
  • 순환
    
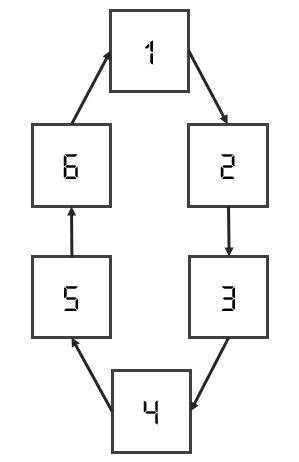
    초기상태가 1이라면, 그 다음 상태는 2가 될 것이고 3 → 4 → 5 → 6 → 다시 1로 계속해서 반복될 것이다.
    
    
  • 독립적인 순환 패턴 여러개
    
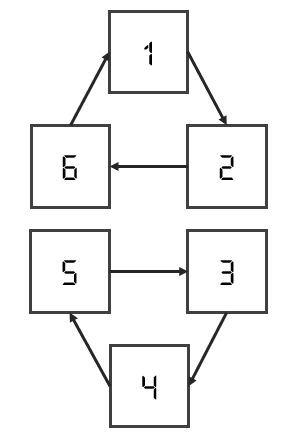
    • 초기상태가 1이라면, 그 다음 상태는 2 → 6 → 1로 반복되며, 3, 4, 5의 상태는 될 수 없다.
    • 초기상태가 3이라면, 그 다음 상태는 4 → 5 → 3으로 반복되며, 1, 2, 6의 상태는 될 수 없다.

• 가역과 비가역

  • 비가역적인 계
    

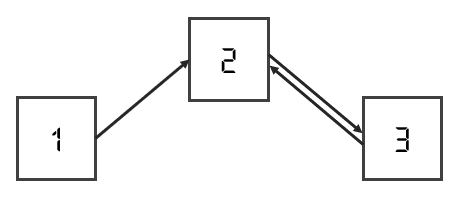
    • 만약 현재 상태가 1이라면, 그 이전의 상태는 존재하지 않는다.
    • 만약 현재 상태가 2라면, 그 이전의 상태는 1이 될 수도, 3이 될 수도 있다.

  • 가역적인 계
    

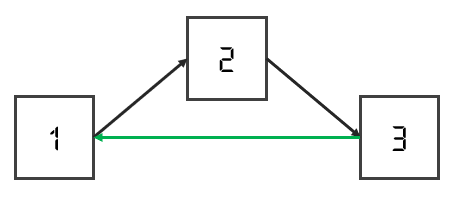
✅ 위에서 보여준 불연속적인 동역학적 계를 무한히 많은 상태가 존재하는 연속적인 계로 확장하면, 그것이 바로 우리가 실제 일상생활에서 확인할 수 있는 보다 현실적인 동역학적 계가 된다.

🔍고전 물리학의 모순

피에르 사몽 라플라스

18세기의 프랑스 물리학자인 피에르 사몽 라플라스는 다음과 같은 말을 남겼다.

우리는 우주의 현재 상태를 과거의 결과로 그리고 미래의 원인으로 간주할 수 있다. 어느 순간 자연을 움직이는 모든 힘과 자연을 구성하는 모든 항목들의 모든 위치를 아는 어떤 지적 존재가 있다고 하자. 게다가 그 지능이 이 모든 데이터를 분석해서 처리할 만큼 충분히 위대하다면, 우주에서 가장 큰 물체의 운동과 가장 미세한 원자의 운동까지도 하나의 공식 속에 아루르게 될 것이다. 그러한 지적 존재에게는 그 어떤 것도 불확실하지 않으며, 미래는 과거와 마찬가지로 눈앞에 펼쳐져 있을 것이다.


- 피에르 사몽 라플라스(Pierre Simon Laplace)

한계

라플라스의 주장이 실제로는 불가능한 가장 큰 이유는 바로 해상도 때문이다.

무한히 많은 상태가 존재하는 상태공간은 연속적인 공간이기 때문에, 아무리 우리가 해당 상태를 확대하여 관찰한다 하더라도 해상도는 유한하기 떄문에 그 상태에 대해서 정확한 값을 말할 수 없다.

따라서 이런 해상도의 문제때문에 우리는 초기조건에 대한 정확한 값을 알 수 없고, 이런 사소한 오차가 혼돈(Chaos)을 가져온다.

📐 막간 - 공간, 삼각법, 벡터

공간과 시간

좌표

• 어떤 공간상에 위치한 점을 명확하게 기술하기 위해서 필요하다.

• 좌표계 잡는 방법 *데카르트 좌표계

  • 원점을 지정한다.

  • 3개의 좌표축(서로 수직)을 지정한다.

    ⇒ 이떄 원점과 좌표축은 다소 ‘임의적’이다. 원점을 어디로 잡던지 상관없으나, 변하지만 않으면 되고 좌표축 또한 원점을 기준으로 어떤 방향으로 잡아도 상관없으나, 서로 수직임을 이루고 변화하지 않으면 된다.

시간

• 시간 또한 원점, 0에서 시작한다.
• 보통 미래를 양의 방향, 과거를 음의 방향으로 잡는다.
• 고전역학의 시간에 대한 가정
  • 시간은 균일하게 흘러간다.
  • 다른 위치에 있더라도, 시간을 비교할 수 있다. (다른 위치여도 시간은 동일)

기준좌표계

• 공간을 나타내는 $x, y, z$ 축과 시간을 나타내는 $t$축을 사용한 하나의 기준 좌표계
• $t$축에 해당하는모든 시간들에 대해 좌표계가 값을 가지고 이를 연속적으로 이으면 우리는 $t$에 대한 함수를 얻을 수 있다.

삼각법 (rad)

rad의 정의

어떤 원의 반지름과 똑같은 길이의 호에 대응되는 각도

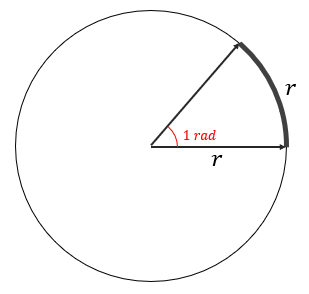
라디안과 도

$1°= { π \over 180 }\ rad$
$360° = 2π\ rad$

(+ 기초 삼각함수관련 내용은 생략 / 수식만 수식노트에 정리)

벡터

벡터

공간에서 길이와 방향을 모두 가지고 있는 개체

• 벡터의 표현

  • 시각화 : 길이와 방향을 가지는 화살표
  • 기호 : 문자위에 화살표 표현
    + 크기는 벡터 기호에 절댓값

• 벡터의 기저 벡터 분해

  • 벡터는 해당 벡터가 위치한 좌표계의 각 축의 성분의 형태로 기술할 수 있다.
  • 각 축을 따라 놓인 길이가 1인 벡터를 단위벡터라고 한다.
  • 벡터는 이런 각각의 성분으로 표현된 벡터들의 선형결합으로 표현할 수 있다.

📌 해당 차원의 좌표계에 위치한 모든 벡터는 그 좌표계를 이루는 기저 단위 벡터(basis)들의 선형결합으로 표현할 수 있다.

벡터의 연산

• 벡터의 스칼라 곱

  • 양수 스칼라 : 스칼라 값만큼 벡터의 길이가 늘어남
  • 음수 스칼라 : 스칼라 값의 절댓값 만큼 벡터의 길이가 늘어나고, 방향이 반대로 바뀜

• 벡터의 덧셈과 뺄셈

  • 평행사변형법
    

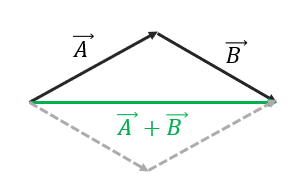
  • 벡터의 뺄셈은 음수 스칼라를 곱한 벡터를 더한다는 개념으로 생각

    $a - b ⇒ a + (-b)$

• 벡터의 내적

  • 벡터 내적의 결과는 스칼라 값이다.
    $A⋅B = |A||B|cosθ$
  • 각 벡터를 이루는 성분들끼리 곱한 결과의 합
  
  

본 포스팅은 레너드 서스킨드의 물리의 정석 - 고전 역학편을 기반으로 작성되었습니다.