거품 정렬, 선택 정렬 , 삽입 정렬 , (합병 정렬, 퀵 정렬, 힙 정렬) , 이분 탐색, dfs, bfs, 동적 계획법
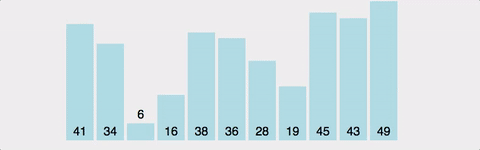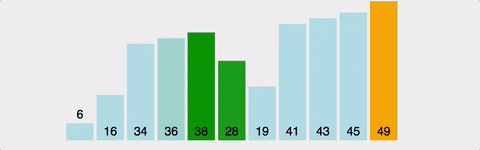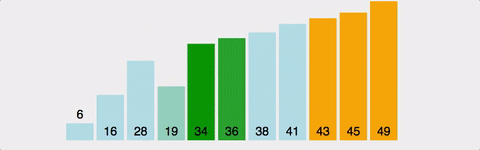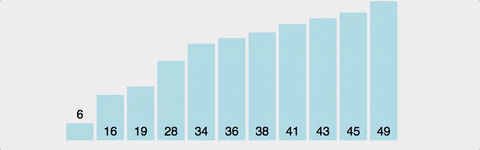
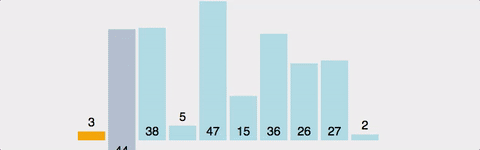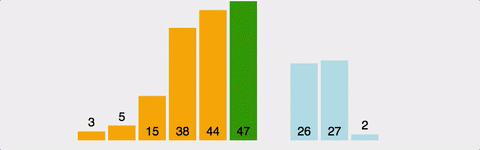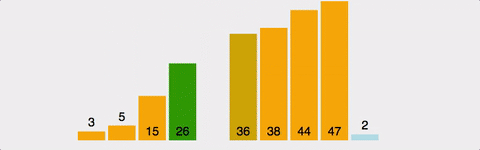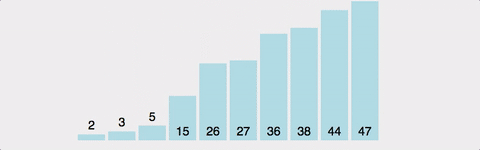
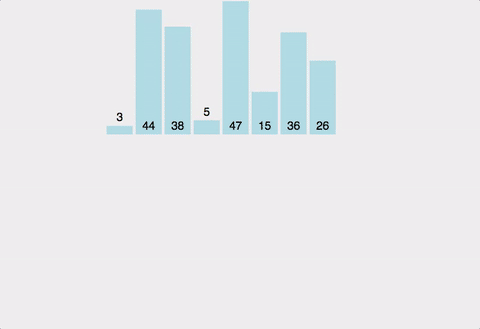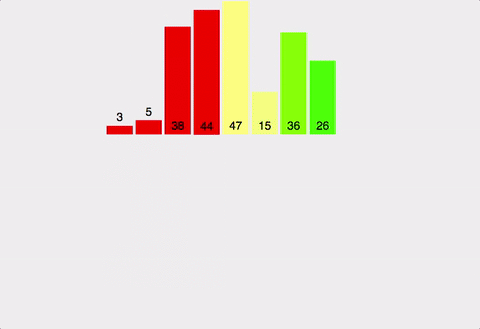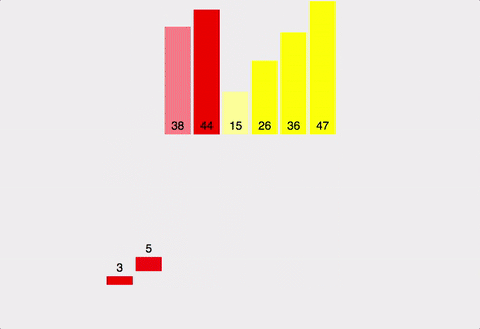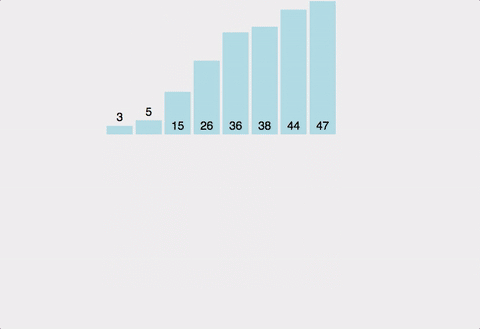
- 버블 정렬 Bubble Sort
- 정렬 알고리즘 중 가장 직관적
- Bubble Sort 는 Selection Sort 와 유사한 알고리즘으로 서로 인접한 두 원소의 대소를 비교하고, 조건에 맞않다면 자리를 교환하며 정렬하는 알고리즘
- 정렬 과정에서 원소의 이동이 거품이 수면으로 올라오는 듯한 모습을 보여 거품 정렬이라 불림
1-1. 정렬 방식
- 오름차순
- 1회전에 첫 번째 원소와 두 번쨰 원소를, 두 번째 원소와 세번째 원소를, n-1 번쨰 원소와 n번째 원소를 비교하여 조건에 맞지 않는다면 서로 교환
- 1회전을 수행하고 나면 가장 큰 원소가 맨 뒤로 이동하므로 2회전에서는 맨 끝에 있는 원소는 정렬에서 제외되고, 2회전을 수행하고 나면 끝에서 2번째 원소까지 정렬에서 제외되게 됨. 이렇게 정렬을 1회전 수행할 때마다 정렬에서 제외되는 데이터가 하나씩 늘어남
- bubble sort 방식
1-2. 시간 복잡도
- (n-1) + (n-2) + (n-3) + ... + 2 + 1 => n(n-1)/2 이므로, O(n^2)
- Bubble Sort는 정렬이 되어있건 안 되어있건 무조건 2개의 원소를 비교하기 때문에 최선, 평균, 최악의 경우 모든 시간 복잡도가 O(n^2)으로 동일 (개선된 bubble Sort 가 존재하긴 함)
1-3. 장점
- 구현이 매우 간단하고, 소스 코드가 직관적
- 정렬하고자 하는 배열 안에서 교환하는 방식이므로, 다른 메모리 공간을 필요로 하지 않음 (제자리 정렬)
- 안정 정렬
1-4. 단점
- 시간 복잡도가 최악, 최선, 평균 모두 O(n^2)로 굉장히 비효율적이라 할 수 있음
- 정렬 되어있지 않은 원소가 정렬 되었을 때의 자리로 가기 위해서 교환 연산이 많이 일어나게 됨 (swap 연산)
- 힙 정렬 Heap Sort
- 최대 힙 트리나 최소 힙 트리를 구성해 정렬하는 방법
- 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 됨
2-1. 정렬 과정
- 정렬해야 할 n개의 요소들로 최대 힙(완전 이진 트리 형태)를 만듦
- 내림차순을 기준으로 정렬
- 그 다음으로 한 번에 하나씩 요소들을 힙에서 꺼내서 배열의 뒤부터 저장
- 삭제되는 요소들(최댓값부터 삭제)은 값이 감소되는 순서로 정렬되게 됨
** 힙 : 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조로 최댓값, 최솟값을 쉽게 추출할 수 있는 자료구조
2-2. 정렬 방식
- 내림차순
- 힙은 1차원 배열로 쉽게 구현 가능
- 정렬해야 할 n개의 요소들을 1차원 배열에 기억한 후 최대 힙 삽입을 통해 차례대로 삽입
- 최대 힙으로 구성된 배열에서 최댓값부터 삭제
2-2 (1) 최대 힙의 삽입
- 힙에 새로운 요소가 들어오면 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입
- 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족 시킴 (부모 노드가 더 작을 시 교환하는 방식으로 진행)
2-2 (2) 최대 힙의 삭제
- 최대 힙에서 최댓값은 루트 노드이므로 루트 노드가 삭제됨
- 최대 힙에서 삭제 연산은 최댓값을 가진 요소를 삭제하는 것
- 삭제된 루트 노드에는 힙의 마지막 노드를 가져옴
- 힙을 재구성
2-3. 시간 복잡도
- 힙 트리의 전체 높이가 거의 log₂n(완전 이진 트리)이므로 하나의 요소를 힙에 삽입하거나 삭제할 때 힙을 재정비하는 시간이 log₂n만큼 소요됨
- 요소의 개수가 n개 이므로 전체적으로 O(log₂n)의 시간이 걸림
2-4. 장점 (유용한 순간)
- 가장 크거나 가장 작은 값을 구할 때 (최소 힙 or 최대 힙의 루트 값이기 때문에 한번의 힙 구성을 통해 구하는 것이 가능)
- 최대 k만큼 떨어진 요소들을 정렬할 때 (삽입 정렬보다 더욱 개선된 결과를 얻어낼 수 있음)
- 삽입 정렬 Insertion Sort
- Selection Sort와 유사하지만 좀 더 효율적인 정렬 알고리즘
- 2번쨰 원소부터 시작하여 그 앞(왼쪽) 원소들과 비교하여 삽입할 위치를 지정한 후, 원소를 뒤로 옮기고 지정된 자리에 자료를 삽입하여 정렬하는 알고리즘
3-1. 정렬 방식(오름차순)
- 첫 번째 원소 앞에는 어떤 원소도 갖고 있지 않기 때문에 두번째 위치(index)부터 탐색을 시작
- temp에 임시로 현재 해당 위치 (index)값을 저장하고, prev에는 해당 위치의 이전 위치 (index-1)을 저장
- prev가 음수가 되지 않고, prev를 인덱스로 갖는 값이 현재 값(temp)보다 크다면 서로 값을 교환해주고 prev를 더 이전 위치를 (prev--1) 가르키게 함
- 위 과정을 끝내면 prev는 현재 temp 값보다 작은 값들 중 제일 큰 값의 위치를 가르키게 됨
- prev+1의 위치에 temp 값을 삽입
3-2. 시간 복잡도
- 최악의 경우 selection sort와 마찬가지로 (n-1) + (n-2) + .... + 2 + 1 => n(n-1)/2 이므로 O(n^2)
- but 모두 정렬이 되어 있는 경우 (Optimal) 한 경우 한번씩 밖에 비교를 안 하므로 O(n)의 시간 복잡도를 가짐
- (이미 정렬되어 있는 배열에 자료를 하나씩 삽입/삭제 하는 경우, 탐색을 제외한 오버헤드가 매우 적기 때문에 최고의 정렬 알고리즘이라 할 수 있음)
3-3. 장점
- 알고리즘이 단순
- 대부분의 원소가 이미 정렬되어 있는 경우, 매우 효율적
- 정렬하고자 하는 배열 안에서 교환하는 방식으로 다른 메모리 공감을 필요로 하지 않음 (제자리 정렬)
- 안정 정렬
** 안정 정렬 : 정렬 시 중복된 값을 입력 순서와 동일하게 정렬하는 알고리즘 (반대의 경우 불안정)
3-4. 단점
- 평균과 최악의 시간 복잡도가 O(n*2)으로 비효율적
- bubble sort와 selection sort와 마찬가지로, 배열의 길이가 길어질 수록 비효율적
** k+1의 요소를 찾기 위해 나머지 모든 요소들을 탐색하는 selection sort와 비교했을 때 k+1번쨰 요소를 배치하는데 필요한 만큼의 요소만 탐색하는 insert sort가 훨 효율적으로 실행된다 볼 수 있음
- 합병 정렬 Merge Sort
- 대표적인 NlogN 정렬 알고리즘
- 항상 NlogN의 성능을 내는 알고리즘으로 힙 정렬과 같고 최악의 상황의 퀵(n^2)보다 안정적
- 평균적으로 퀵 정렬보다 느린 성능을 보이며 알고리즘 구현에 있어 힙 정렬보다 메모리를 더 많이 사용
- 일반적인 방법으로 구현했을 때 이 정렬은 안정 정렬에 속하며, 분할 정복 알고리즘의 하나
(안정 정렬, 분할 정복 알고리즘 정리하기)
4-1. 정렬 과정
- 리스트 길이가 0 또는 1이면 이미 정렬된 것으로 간주
- 그렇지 않은 경우, 정렬되지 않은 리스트를 절반으로 잘라 비슷한 크기의 두 부분 리스트로 나눔
- 각 부분 리스트를 재귀적으로 합병 절렬을 이용해 정렬
- 두 부분 리스트를 다시 하나의 정렬된 리스트로 합병
** 퀵 정렬과의 차이점 정리
4-2. 정렬 방식 (오름차순)
- 무작위로 저장된 2개의 배열을 처음부터 하나씩 비교하여 더 작은 값을 새로운 리스트로 옮김
- 둘 중 하나가 끝날 때 까지 이 과정을 반복
- 만약 둘 중 하나의 리스트가 먼저 끝나게 된다면 나머리 리스트의 값들을 전부 새로운 리스트로 복사
- 새로운 리스트를 원래의 리스트로 옮김
4-3. 시간 복잡도
- nlog₂n(비교) + 2nlog₂n(이동) = 3nlog₂n = O(nlog₂n)
4-4. 장점
- 안정적인 정렬이 가능
- 데이터의 분포의 영향을 덜 받음 (입력 데이터가 무엇이든 정렬되는 시간이 동일)
- 만약 레코드를 연결 리스트로 구성하면, 링크 인덱스만 변경되므로 데이터의 이동은 무시할 수 있을 정도로 작아짐 (제자리 정렬로 구현 가능)
- 크기가 큰 레코드를 정렬할 경우 연결 리스트를 사용한다면, 합병 정렬은 퀵 정렬을 포함한 어떤 정렬보다 효율적
4-5. 단점
- 만약 레코드를 배열로 구성한다면, 임시 배열이 필요 (제자리 정렬이 아님)
- 레코드들의 크기가 큰 경우에는 이동 횟수가 많으므로 매우 큰 시간적 낭비를 초례
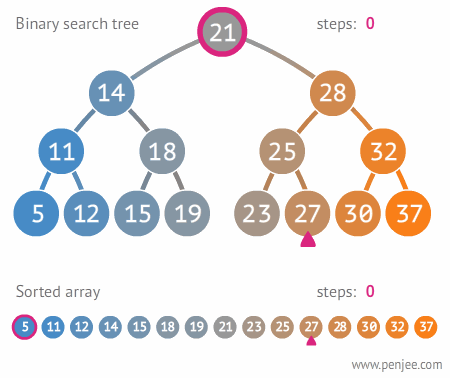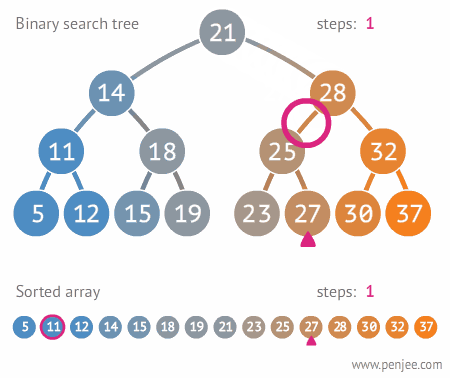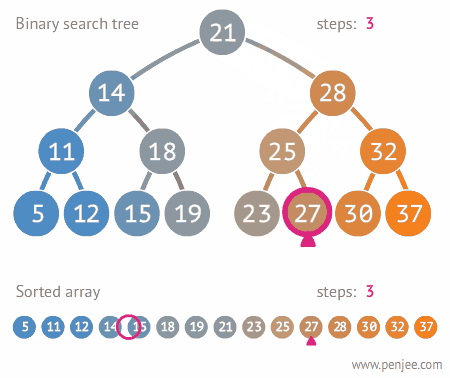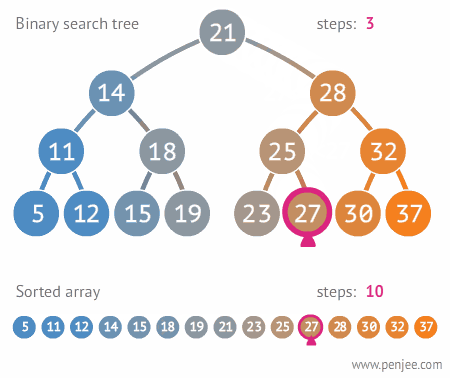
7. 이분탐색
- 처음부터 끝까지 돌면서 탐색하는 것보다 훨씬 빠르다는 장점을 지님
- (전체 탐색 O(N) , 이분 탐색 O(logN))
7-1. 진행 순서
- 배열을 정렬 시킴
- first와 last 로 mid 값 설정
- mid와 내가 구하고자 하는 값 비교
- 구할 값이 mid 보다 높으면 --> first = mid+1 , 구할 값이 mid 보다 낮으면 --> last = mid -1
- first > last 가 될 때까지 계속 반복하기
7-2. 예제 코드 (java)
public static int binarySearch(int[] A, int n) {
int first = 0;
int last = A.length - 1;
int mid = 0;
while (first <= last) {
mid = (first + last) / 2;
if (n == A[mid])
return 1;
else {
if (n < A[mid])
last = mid - 1;
else
first = mid + 1;
}
}
return 0;
}
- 깊이 우선 탐색 DFS
- 갈 수 있는 만큼 최대한 깊이 가고, 더 이상 갈 곳이 없으면 이전 정점으로 돌아가는 것
- stack과 재귀 함수를 사용하여 구현
8-1. 장점
- 현 경로 상의 노드들만 기억하면 되므로 저장공간 수요가 비교적 적음
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있음
8-2. 단점
- 해가 없는 경로가 깊을 경우 탐색 시간이 오래 걸릴 수 있음
- 얻어진 해가 최단 경로가 된다는 보장이 없음
- 깊이가 무한하게 깊어지면 스택 오버 플로우가 날 위험이 있음 (깊이 제한을 두는 방법으로 해결 가능)
8-3. 구현
- 인접 행렬로 구현했는지 인접 리스트로 구현했는지에 따라 구현 방법 상이
인접 행렬 : 그래프의 정점을 2차원 배열로 만든 것, 정점의 개수가 n이라면 n*n 형태의 2차원 배열이 인접 행렬로 사용 됨 , 행과 열은 정점, 각 원소들은 정점 간의 간선을 나타냄
인접 리스트 : 각 정점에 인접한 정점들을 연결리스트로 표현한 방법, 정점의 개수만큼 인접리스트가 존재
(1) 인접 행렬로 구현 했을 경우
int[][] adjArray = new int[n+1][n+1];
// 두 정점 사이에 여러 개의 간선이 있을 수 있다.
// 입력으로 주어지는 간선은 양방향이다.
for(int i = 0; i < m; i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
adjArray[v1][v2] = 1;
adjArray[v2][v1] = 1;}
System.out.println("DFS - 인접행렬 / 재귀로 구현");
dfs_array_recursion(v, adjArray, visited);
Arrays.fill(visited, false); // 스택 DFS를 위해 visited 배열 초기화
System.out.println("\n\nDFS - 인접행렬 / 스택으로 구현");
dfs_array_stack(v, adjArray, visited, true);
- 시간 복잡도 : dfs 하나 당 N번의 loop를 돌게 되므로 O(n)의 시간 복잡도를 가짐 , 여기서 N개의 정점을 모두 방문해야하므로 n*O(n)
--> 인접행렬로 구현 했을 경우 O(n^2)의 시간 복잡도를 가짐
> #### (2) 인접 리스트로 구현했을 경우LinkedList[] adjList = new LinkedList[n + 1];
for (int i = 0; i <= n; i++) {
adjList[i] = new LinkedList();
}
// 두 정점 사이에 여러 개의 간선이 있을 수 있다.
// 입력으로 주어지는 간선은 양방향이다.
for (int i = 0; i < m; i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
adjList[v1].add(v2);
adjList[v2].add(v1);
}
for (int i = 1; i <= n; i++) { // 방문 순서를 위해 오름차순 정렬
Collections.sort(adjList[i]);
}
System.out.println("DFS - 인접리스트");
dfs_list(v, adjList, c);
> #### (2) 인접 리스트로 구현했을 경우 (재귀)public static void dfs_list(int v, LinkedList[] adjList, boolean[] visited) {
visited[v] = true; // 정점 방문 표시
System.out.print(v + " "); // 정점 출력
Iterator<Integer> iter = adjList[v].listIterator(); // 정점 인접리스트 순회
while (iter.hasNext()) {
int w = iter.next();
if (!visited[w]) // 방문하지 않은 정점이라면
dfs_list(w, adjList, visited); // 다시 DFS
}}
- 시간 복잡도 : dfs가 총 N번 호출되긴하나 인접 행렬과 달리 인접 리스트로 구현하게 되면 dfs 하나당 각 정점에 연결되어 있는 간선의 개수만큼 탐색을 하므로 예측이 불가능 , but dfs가 끝난 후를 생각하면 모든 정점을 한번씩 다 방문하고 모든 간선을 한번씩 다 검사했다 볼 수 있으므로 O(n+e)의 시간이 걸렸다고 할 수 있음
--> 인접 리스트로 구현했을 경우 O(n+e)의 시간 복잡도를 가짐
<br>
> ### 9. 너비 우선 탐색 BFS
- queue를 이횽하여 지금 위치에 갈 수 있는 정점을 모두 queue에 넣는 것
### 9-1. 장점
- 너비를 우선으로 탐색하므로 답이 되는 경로가 여러개인 경우에도 최단 경로를 얻을 수 있음
- 경로가 무한하게 깊어져도 최단 경로를 반드시 찾을 수 있음
- 노드 수가 적고 깊이가 얕은 해가 존재할 때 유리
### 9-2. 단점
- dfs와 달리 큐를 이용하여 다음에 탐색할 정점들을 저장하므로 더 큰 저장 공간이 필요함
### 9-3. 구현
- 인접 행렬로 구현했는지 인접 리스트로 구현했는지에 따라 구현 방법 상이
> #### (1) 인접행렬로 구현했을 경우int[][] adjArray = new int[n+1][n+1];
// 두 정점 사이에 여러 개의 간선이 있을 수 있다.
// 입력으로 주어지는 간선은 양방향이다.
for(int i = 0; i < m; i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
adjArray[v1][v2] = 1;
adjArray[v2][v1] = 1;}
System.out.println("BFS - 인접행렬");
bfs_array(v, adjArray, visited);
public static void bfs_array(int v, int[][] adjArray, boolean[] visited) {
Queue q = new LinkedList<>();
int n = adjArray.length - 1;
q.add(v);
visited[v] = true;
while (!q.isEmpty()) {
v = q.poll();
System.out.print(v + " ");
for (int i = 1; i <= n; i++) {
if (adjArray[v][i] == 1 && !visited[i]) {
q.add(i);
visited[i] = true;
}
}
}}
- 시간 복잡도 : 정점 한개당 N번의 for loop를 돌기 때문에 O(n)의 시간이 걸림, 이 for loop는 큐에 아무것도 없을 때 까지 (== 모든 정점을 방문할 때까지) 실행되므로 n번 반복 실행됨
--> 인접 행렬로 구현했을 경우 O(n^2) 시간 복잡도를 가짐
> #### (2) 인접 리스트로 구현했을 경우LinkedList[] adjList = new LinkedList[n + 1];
for (int i = 0; i <= n; i++) {
adjList[i] = new LinkedList();
}
// 두 정점 사이에 여러 개의 간선이 있을 수 있다.
// 입력으로 주어지는 간선은 양방향이다.
for (int i = 0; i < m; i++) {
int v1 = sc.nextInt();
int v2 = sc.nextInt();
adjList[v1].add(v2);
adjList[v2].add(v1);
}
for (int i = 1; i <= n; i++) {
Collections.sort(adjList[i]); // 방문 순서를 위해 오름차순 정렬
}
System.out.println("BFS - 인접리스트");
bfs_list(v, adjList, visited);
public static void bfs_list(int v, LinkedList[] adjList, boolean[] visited) {
Queue queue = new LinkedList();
visited[v] = true;
queue.add(v);
while(queue.size() != 0) {
v = queue.poll();
System.out.print(v + " ");
Iterator<Integer> iter = adjList[v].listIterator();
while(iter.hasNext()) {
int w = iter.next();
if(!visited[w]) {
visited[w] = true;
queue.add(w);
}
}
}}
- 시간 복잡도 : 리스트로 구현된 dfs와 비슷한 논리로 시간 복잡도를 구하게 됨, bfs를 다 끝낸 후를 생각하면 모든 간선에 대해 한번씩 검사를 하고 각 정점을 한번씩 모두 방문
--> 인접리스트로 구현했을 경우 O(n+e)의 시간 복잡도를 가짐
==> 두 알고리즘 모두 인접행렬을 사용하여 만든 그래프의 경우에는 O(n^2)의 시간복잡도를 가지고 인접리스트를 사용하여 만든 그래프의 경우에는 O(n+e)의 시간복잡도를 가짐
<br>
> ### 10. 동적 계획 법 ( DP - Dynamic Programming )
- 큰 문제를 작은 문제로 나누고 작은 문제들의 답을 이용해 큰 문제의 답을 구하는 방법론
- 이전 문제의 답을 기억하면서 푸는 것이라 할 수 있음 (memorization)
- dp 문제는 재귀 문제와 매우 비슷한데 일반적 재귀와 달리 dp를 사용하면 한 번 계산한 문제의 답을 다시 계산하지 않아도 되기 때문에 시간을 단축할 수 있음
### 10-1. 조건
- 최적 부분 구조 : 큰 문제의 답에 작은 문제의 답이 포함되어 있는 것
- 부분 문제 반복 : 한 번 구했던 답이 나중에도 사용되며 이 답은 변하지 않아야 한다는 것
ex) 피보나치 수열
### 10-2. 풀이 종류
#### (1) Bottom-Up
- 작은 문제부터 해결하는 것
- 보통 for 문을 사용해 재귀 없이 해결하여 시간과 메모리를 절약할 수 있다는 장점이 있음
- but 직관적으로 이해하기 힘들 수 있다는 단점 존재
ex ) dp 테이블 초기화 , 피보나치를 예를 들면 1, 2는 구할 수 없으니 초기화 해준 뒤 for문을 통해 3부터(작은 문제) 시작해서 점화식을 이용해 n까지 채워나가는 경우def fibonacci_dp(num):
f = [0, 1]
for i in range(2, num+1):
f.append(f[i-1] + f[i-2])
return f
#### (2) Top-Down
- 큰 문제에서 부터 작은 문제로 내려가면서 큰 문제의 답을 구하는 방법
- 보통 재귀로 문제 해결
- 재귀를 돌면서 전에 계산해둔 값이 있으면 쓰고 없으면 계산하는 식
- 최대 재귀 깊이 초과 에러가 발생할 수 있으며 메모리와 시간을 bottom-up에 비해 많이 잡아 먹는다는 단점이 있음
- but 점화식을 이해하기 쉽다는 장점도 존재
ex) memorization할 수 있는 리스트 초기화 후 피보나치 함수를 재귀로 구현한 뒤 게산한 값이 있으면 값을 반환 없다면 점화식에 따라 피보나치 결과를 반환하는 방식으로 재귀 함수에 n(큰 문제)를 매개변수로 넘겨주고 재귀를 돌리는 방식의 경우def fibonacci_memori(num):
global memo
if num >= 2 and len(memo) <= num:
memo.append(fibonacci_memori(num-1) + fibonacci_memori(num-2))
return memo[num]
memo = [0, 1]
### 10-3. 비교 ?
- 더 좋은 방법을 명확히 택하기 어렵지만 dp 풀이 방식은 top-down이 자연스러운 접근이 가능한 경우가 많음
but 효율성을 고려할 경우 bottom-up 을 사용하는 것이 더 좋음
- 하위 문제가 복잡하여 점화식으로 풀어낼 방법이 떠오르지 않을 경우에도 top-down으로 접근하는 경우가 많음
### 10-4. DP 문제
1) 문제 구별
(1) 큰 문제의 답에 작은 문제의 답이 포함되어 있는지
- 재귀 스러운 문제인가 ?
- 큰 문제를 같은 형태의 작은 문제로 나눌 수 있는가 ?
(2) 하위 문제의 계산이 반복되는지
- 한 번 구했던 문제의 답이 나중에도 사용되는가 ?
- 작은 문제의 답은 항상 같은가 ?
(3) 최적화, 최대화, 최소화, 경우의 수를 구하는 유형인지
- 위의 두 개를 생각해 봤는데도 헷갈릴 경우 생각해보기
- 보통 이런 유형의 문제일 때 dp로 푸는 경우가 많음
2) DP vs 완전탐색 vs 그리디
(1) 그리디
- 현재 선택 지 중에서 가장 좋은 방법만 선택
- 작은 문제를 풀 때 그 상황에서 가장 좋아보이는 것만 선택해도 큰 문제를 풀 수 있을 때
- 내가 생각한 딱 하나의 최적의 방법이 끝까지 반례 없이 적용될 때
(2) 완전탐색
- 모든 경우의 수를 탐색
- 아무런 규칙이 없어서 모든 경우의 수를 탐색해야 할 때
==> 완전 탐색이라기엔 시간이 부족하고 그리디라하기엔 항상 탐욕적으로 취해서는 답이 나오지 않는 경우 dp
3) 풀이 방법
- 문제의 조건대로 손으로 그려보며 반복 되는 부분 찾기
- dp테이블 dp[i]는 무엇을 의미하는지 정의
- 디테일한 점화식 설계( dp[i] = dp[i+1] + dp[i-2] )
- 필요에 따라 dp 테이블 확장 ( dp[i] --> dp[i][j] )
- 중복되는 부분을 어떻게 활용할수 있을지 고민 ( 어떤 방법으로도 점화식이 세워지지 않을 경우 계산 과정이나 정의의 순서를 뒤집어 생각 ) ex 1+1 = 2 x 2 = 1 + 1 로 두고 위 과정 반복
4) 에시 문제 (백준 1로 만들기 #1463)n = int(input()) # 1로 만들 값
d = [0] * (N+1) # memorization
for i in range(2, n+1):
d[i] = d[i-1] + 1 # i라는 수의 1까지 최소 연산 횟수는 그 전의 수의 최소 연산 횟수 + 1회
if i % 2 == 0:
# i라는 수의 최소 연산 횟수는 그 전의 수의 최소 연산 횟수 + 1회,
# i를 2로 나눈 수의 최소 연산 횟수 + 1회 중에 최솟값
d[i] = min(d[i], d[i//2] + 1)
if i % 3 == 0:
d[i] = min(d[i], d[i//3] + 1)print(d[n])
알고리즘 문제는 자꾸 파이썬으로 풀어버릇했더니 또 파이썬으로 써놨읍니다 sorry ~
끝