+) 코드잇 강의 바로가기

본 정리내용은 코드잇 강의를 공부하며 함께 정리한 내용입니다! 더 정확하고 자세한 내용을 공부하기 위해서는 "코드잇 머신러닝 실전 강의를 참고해주세요!"

층,뉴런, 가중치, 편향 표기법

층의 갯수

• 층을 세는 방법 : hidden layer, ouput layer 수만 셈
  *input layer는 층이긴 하나 총층 수를 counting할때에는 input layer가 표현되지 않음. 총 층수는 $L = number$와 같이 표기함.
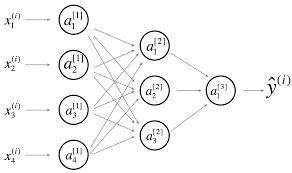
  Ex)
  • 위 인공신경망의 총 층수는 hidden layer 2개, output layer가 1개이므로 $L=3$인 인공신경망이라고 할 수 있다.
• *$n^{[l]}$: n번째 층의 뉴런의 수를 나타내는 기호

뉴런의 출력 표기 방법

• 뉴런의 출력 : 뉴런이 얼마나 활성화 되어있는지 나타냄.
• 뉴런의 출력을 표기할 때 고려할 사항 :
  1. 몇번째 층에 있는지
  2. 그 층안에서 몇번째 위치에 있는 뉴런의 출력인지
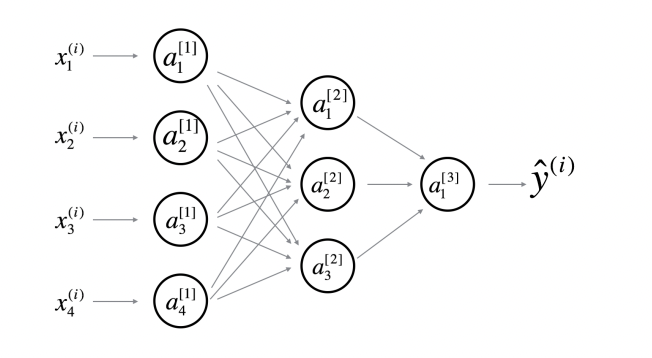
• 뉴련 출력 표현 형식 : l번째층에 있다고 가정한다면, a 로 표기 하며 [l]을 위첨자로 취하여 해당 층의 출력값을 표현 해줌. 그리고 뉴런의 위치는 아래첨자로 오른쪽에 표현함.
  Ex1) $a^{[l]}$ : $l$번째 layer의 출력값 전체
  Ex2) $a^{[l]}_{i}$ : $l$번째 layer의 i번째 위치한 뉴런의 출력
  

가중치 표기 방법

• 가중치란? 가중치는 뉴런의 출력을 계산하는 데 사용되는 입력에 곱해지는 계수로, 전 층 뉴런들의 출력과 곱해지는 값을 말한다. 가중치를 뜻하는 영어 단어 weight의 앞 알파벳 w를 사용해서 나타냄.

• 가중치 표기시 구성 요소 :

1. 층의 위치 (가중치는 두 층 사이를 연결하여 뒤의 층으로 표기)
2. 앞 층에 몇 번째 뉴런과 연결되는지
3. 뒤 층에 몇 번째 뉴런과 연결되는지

• 가중치 표현 형식 : w로 표현하며 []를 위첨자로 두어 i-1번째와 i번째 사이의 weight을 $w^{[i]}$로 층을 표기한다. 그리고 아래첨자로 앞에 연결된 뉴런의 번호 k, 뒤 뉴런의 번호를 j라고 했을때 $(k,j)$를 아래 첨자로 표기한다.
  Ex1) $w^{[l]}$ : $l-1$번째 layer와 $l$번째 layer에 연결된 모든 가중치
  Ex2) $w^{[l]}_{(k,j)}$ : $l-1$번째 layer의 k번째 뉴런과 $l$번째 layer의 j번째 뉴런과 연결된 가중치
  
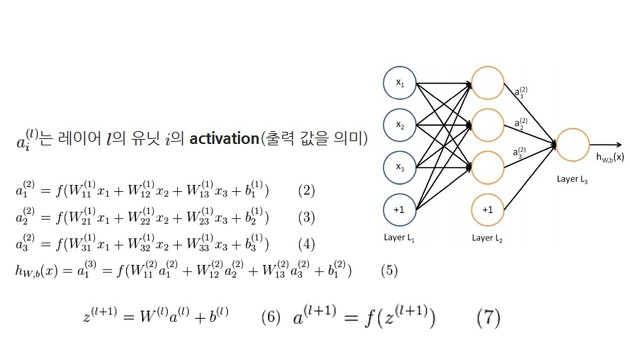
• 가중치 행렬의 요소눈 일반적으로 쓰는 행렬 표현법과는 다름을 유의 (오른쪽 아래 행과 열을 나타내는 위치가 반대)
• 편향 표현 형식 : b로 표현하며 []를 위첨자로 두어 i-1번째와 i번째 사이의 bias을 b[i]로 사용한다.

편향

• 편향도 뉴런의 출력을 계산하는 데 사용되며, 전 층 뉴런의 출력과 가중치의 곱들과 함께 더해지는 값. 편향을 뜻하는 영어 단어 bias의 앞 알파벳 b를 사용해서 나타냄

• 뉴런의 편향을 표기할 때 고려할 사항 :
  1. 몇번째 층에 있는지
  2. 그 층안에서 몇번째 위치에 있는 뉴런의 편향인지
• 뉴련 출력 표현 형식 : l번째층에 있다고 가정한다면, b 로 표기 하며 [l]을 위첨자로 취하여 해당 층의 출력값을 표현 해줌. 그리고 뉴런의 위치는 아래첨자로 오른쪽에 표현함.
  Ex1) $b^{[l]}$ : $l$번째 layer의 편향 전체
  Ex2) $b^{[l]}_{i}$ : $l$번째 layer의 i번째 위치한 뉴런의 편향

MNIST 데이터에서 데이터 표기

입력 변수 : 이미지

• 먼저 입력 변수는 변수 X 사용
• 여러가지 데이터 요소 및 이미지 갯수를 표현할 방법이 필요함

1. 몇 번째 이미지의 데이터인지 (행)
2. 몇 번째 픽셀의 데이터인지 (열)

• 표기법 : 몇 번째 이미지의 데이터인지를 x의 윗첨자로 소괄호를 사용해서 표기하고, 몇 번째 픽셀의 데이터인지를 아래첨자로 숫자를 써서 표기한다.
  Ex) $x^{(i)}_j$: i 번째 이미지의 j 번째 픽셀 데이터

목표 변수

• 목표 변수 : 몇번째 숫자인지 태깅
  1.몇 번째 이미지의 데이터인지 (행)
  2.몇 번째 숫자 종류 데이터인지 (열)

• 특징 : 목표 변수에 크기가 생기므로 크기를 없애기 위해서 one-hot encoding을 통해서 1~9까지의 숫자를 벡터의 형태로 변환시켜 숫자 데이터의 대소를 없애줍니다.

• 표기법 : 몇 번째 이미지의 데이터인지를 y의 윗첨자로 소괄호를 사용해서 표기하고, 타겟의 숫자 번호를 아래첨자로 숫자를 써서 표기한다.
  Ex) $x^{(i)}_j$: i 번째 이미지의 타겟 값이 j인지 아닌지 확인하는 원소값.

순전파(Forward Propagation)

인공신경망에서 순전파는 입력층으로 들어오는 정보가 층 단위로 마지막 층까지 처리 및 계산되어 출력되는 과정이며 주로 예측값을 출력하는 과정으로 많이 쓰인다. Feedforward 또는 forward Propagation이라고 부른다.

• 뉴런 출력 계산
  Hidden layer, Output layer:
  • Step 1. z = 전 층 모든 뉴런의 출력 X 가중치 + 편향
  • Step 2. a = 계산한 z를 시그모이드 활성 함수에 대입
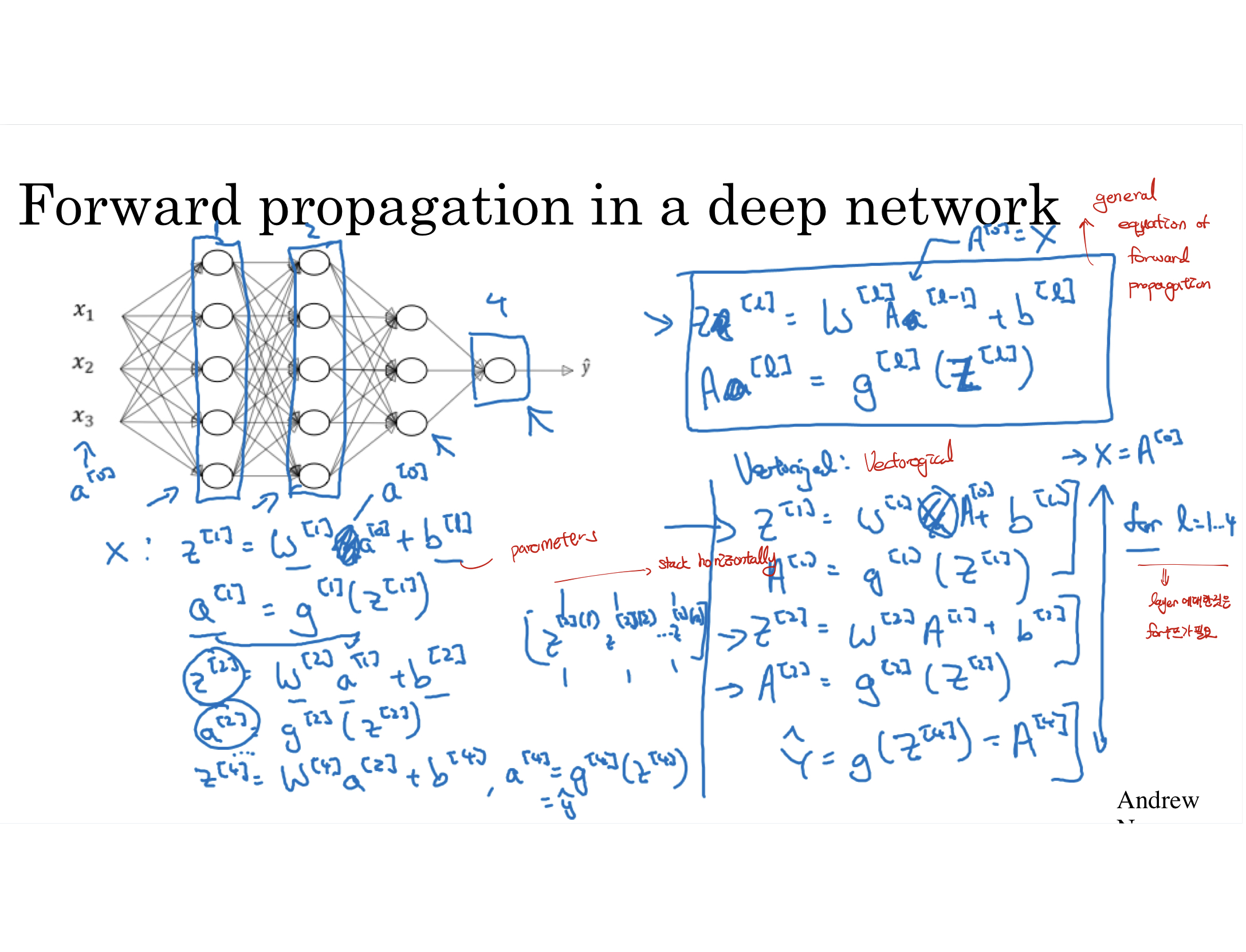
• 순전파의 계산 : 입력층에서 입력을 받아 가중치와 편향을 이용해서 연산을 하고, 활성화 함수에 대입하여 최종 출력값을 구해줍니다. 그리고 이 출력값을 이용하여 다음 층의 입력으로 활용하여 진행해주고 이 방식을 0번째 층부터 순서대로 1, 2, 3, 4, ... l번째 layer까지 진행하여 최종 출력값을 계산해준다.
• 행렬 식 :
  $Z^{[i]}=W^{[i]}\times a^{[i-1]} +b^{[i]}$
  $a^{[i]}= \sigma(Z^{[i]})$
  

가설함수 손실함수 조건
1. 현재 가중치와 편향을 가지고 입력 변수에 대해 예측
2. 가중치와 편향으로 한 예측이 얼마나 좋거나 안 좋은지를 판단할 수 있어야 함.

가설함수

• 인공신경망에서 가설함수란? 가설 함수는 주어진 가중치와 편향에 따라 마지막 층 뉴런들의 출력을 계산해내는 함수
  $h_W(x)=a^{[L]}=σ(W^{[L]}a^{[L-1]}+b^{[L]})$

손실함수

• 신경망에서의 손실함수: 가중치와 편향들로 한 예측이 얼마나 좋은지를 판단하는 함수.(평균제곱오차 활용)
  $J(W)= 1/2mn^{[L]} \times \displaystyle\sum_{i=1}^{m} \displaystyle\sum_{k=1}^{n^{[L]}}(h_W(x^{(i)})_ k−y_k^{(i)})^2$

참고 : 코드잇딥러닝