소프트맥스 회귀(Softmax Regression)
원-핫 인코딩(One-Hot Encoding)
원-핫 인코딩은 선택해야 하는 선택지의 개수만큼의 차원을 가지면서,
각 선택지의 인덱스에 해당하는 원소에는 1, 나머지 원소는 0의 값을 가지도록 하는 표현 방법이다.
예를들어 임의로 강아지는 0번 인덱스, 고양이는 1번 인덱스, 냉장고는 2번 인덱스를 부여하였다고 했을 때
강아지 = [1, 0, 0]
고양이 = [0, 1, 0]
냉장고 = [0, 0, 1]
로 표현할 수 있고 위 벡터는 모두 3차원의 벡터이다.
원-핫 벡터의 무작위성
정수 인코딩을 보자. Banana, Tomato, Apple라는 3개의 클래스에 레이블을 각각 1, 2, 3을 부여해보자.
실제값이 Tomato일때 예측값이 Banana이었다면 제곱 오차는 (2 - 1)^2 = 1
실제값이 Apple일때 예측값이 Banana이었다면 제곱 오차 (3 - 1)^2 = 4
즉, Banana과 Tomato 사이의 오차보다 Banana과 Apple의 오차가 더 크다.
이는 banana가 Apple보다는 Tomato에 더 가깝다는 뜻이다!
그런데 원-핫 인코딩을 통해서 레이블을 인코딩하면 각 클래스 간의 제곱 오차가 균등해진다.
모든 클래스에 대해서 원-핫 인코딩을 통해 얻은 원-핫 벡터들은 모든 쌍에 대해서 유클리드 거리를 구해도 전부 유클리드 거리가 동일하다. 즉 각 클래스의 표현 방법이 무작위성을 가진다는 점을 표현할 수 있다.(그러나 유사성을 구할 수 없다는 단점도 존재한다.)
소프트맥스 회귀(Softmax Regression) 이해하기
앞에서 로지스틱 회귀를 통해 2개의 선택지 중에서 1개를 고르는 이진 분류(Binary Classification)를 보았다.
이번에는 3개 이상의 선택지로부터 1개를 선택하는 문제인 다중 클래스 분류(Multi-Class classification)를 풀기 위한 소프트맥스 회귀를 공부해보자.
다중 클래스 분류(Multi-class Classification)
세 개 이상의 답 중 하나를 고르는 문제를 다중 클래스 분류(Multi-class Classification)라고 한다.
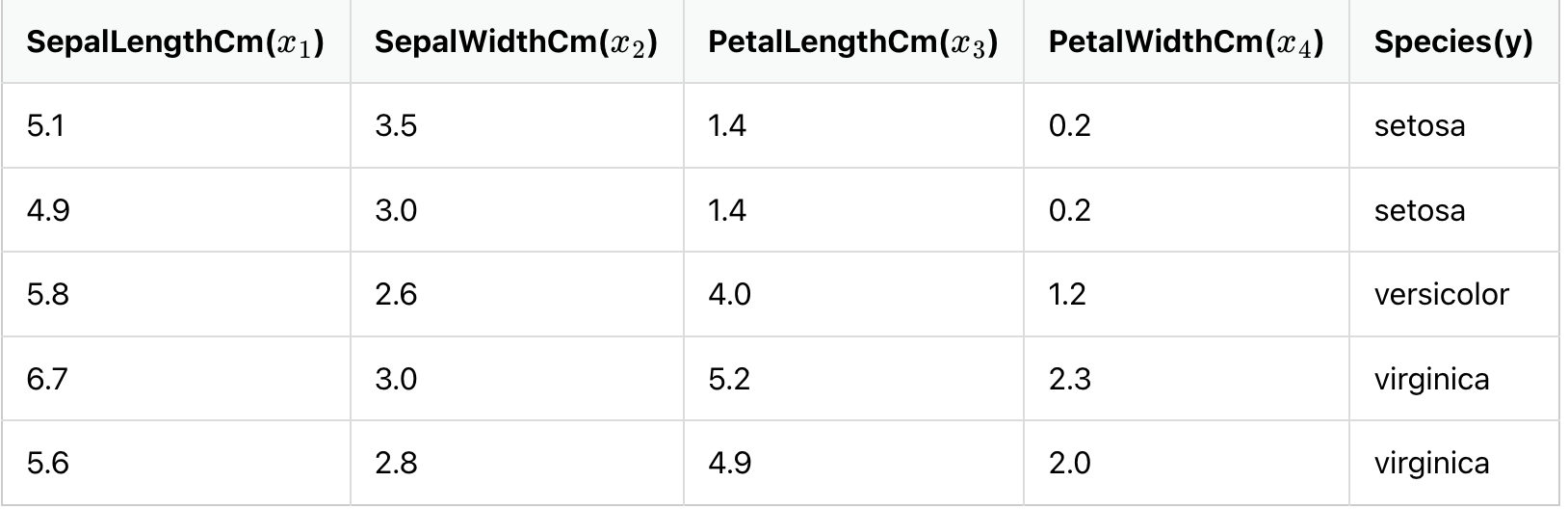
꽃받침 길이, 꽃받침 넓이, 꽃잎 길이, 꽃잎 넓이라는 4개의 특성(feature)로부터 setosa, versicolor, virginica라는 3개의 붓꽃 품종 중 어떤 품종인지를 예측하는 문제를 보자.
로지스틱 회귀에서 시그모이드 함수는 예측값을 0과 1 사이의 값으로 만든다.

소프트맥스 회귀는 각 선택지마다 소수 확률을 할당하고(총 확률의 합은 1) 각 선택지가 정답일 확률로 표현한다.
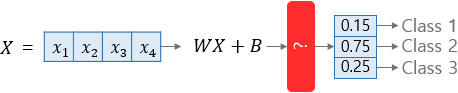
소프트맥스 함수(Softmax function)
분류해야하는 정답지(클래스)의 총 개수를 k라고 할 때, k차원의 벡터를 입력받아 각 클래스에 대한 확률을 추정한다.
k차원의 벡터에서 i번째 원소를 zi, i번째 클래스가 정답일 확률을 pi로 나타낸다고 하였을 때 다음과 같다.
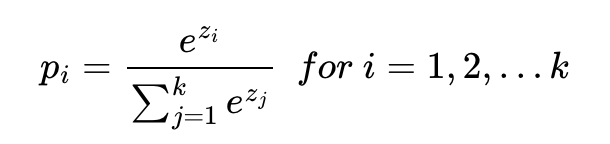
위 문제는 k = 3이므로 z = [z1, z2,z3]의 입력을 받을 때 출력은 다음과같다.
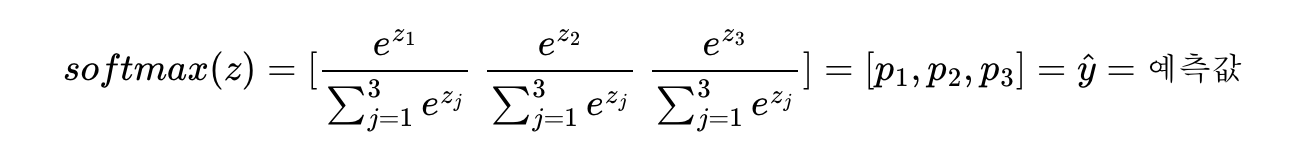
p1,p2,p3은 1번 클래스가 정답일 확률, 2번 클래스가 정답일 확률, 3번 클래스가 정답일 확률을 나타내며 각각 0과 1사이의 값으로 총 합은 1이다.(virginica일 확률, setosa일 확률, versicolor일 확률을 나타내는 값)
그런데 질문 1.
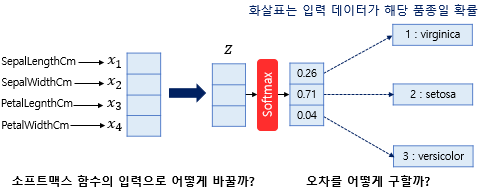
그런데 하나의 샘플 데이터는 4개의 독립 변수 x를 가지고, 이는 모델이 4차원 벡터를 입력으로 받는다는 것이다.
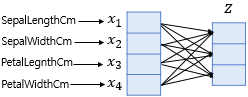
그런데 소프트맥스의 함수의 입력으로 사용되는 벡터는 벡터의 차원이 분류하고자 하는 클래스의 개수가 되어야 하므로 3차원 벡터로 변환되어야 한다.
소프트맥스 함수의 입력 벡터 z의 차원수만큼 결과값의 나오도록 가중치 곱을 진행한다.
위의 그림에서 화살표는 총 (4 × 3 = 12) 12개이며 전부 다른 가중치를 가지고, 학습 과정에서 점차적으로 오차를 최소화하는 가중치로 값이 변경된다.
질문 2
소프트맥스 함수의 출력은 분류하고자하는 클래스의 개수만큼 차원을 가지는 벡터로 각 원소는 0과 1사이의 값(특정 클래스가 정답일 확률)을 가진다.
이 예측값과 비교를 할 수 있는 실제값의 표현 방법이 있어야 하는데 소프트맥스 회귀에서는 실제값을 원-핫 벡터로 표현한다.

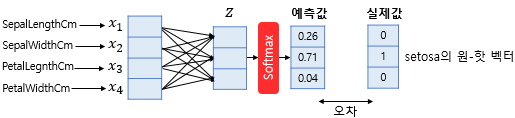
예를 들어 현재 풀고 있는 샘플 데이터의 실제값이 setosa라면 setosa의 원-핫 벡터는 [0 1 0]입니다. 이 경우, 예측값과 실제값의 오차가 0이 되는 경우는 소프트맥스 함수의 결과가 [0 1 0]이 되는 경우이다.
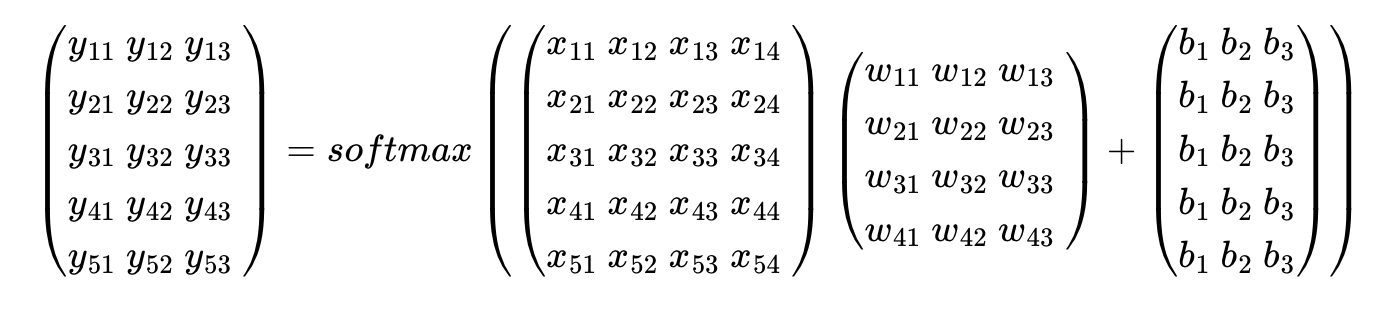
입력을 특성(feature)의 수만큼의 차원을 가진 입력 벡터 x라고 하고, 가중치 행렬을 W, 편향을 b라고 하였을 때, 소프트맥스 회귀에서 예측값을 구하는 과정을 벡터와 행렬 연산으로 표현하면 다음과 같다.
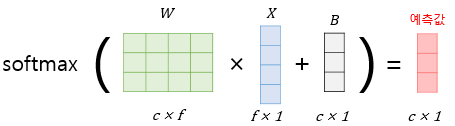
행렬 연산으로 이해하기
위의 예제의 데이터는 전체 샘플의 개수가 5개, 특성이 4개이므로 5 × 4 행렬인데
-
편의상 행렬 X의 원소 위치를 반영한 변수로 표현해보자.
-
그런데 선택지가 총 3개인 문제이므로 가설의 예측값으로 얻는 행렬 yhat의 열의 개수는 3개여야 하고 각 행은 행렬 X의 각 행의 예측값이므로 행의 크기는 동일해야 한다. 즉 결과적으로 행렬 yhat 의 크기는 5 × 3이다.
-
행렬곱에 따라 W은 4 × 3의 크기를 가진 행렬임을 알 수 있다.
-
B는 예측값 행렬 yhat과 크기가 동일해야하므로 5 × 3의 크기를 가진다.
가설식은 yhat = softmax(XW + B)이다.
비용 함수(Cost function)
크로스 엔트로피 함수
y는 실제값, k는 클래스의 개수로 정의한다.
yj는 실제값 원-핫 벡터의 j번째 인덱스를 의미하며,
pj는 샘플 데이터가 j번째 클래스일 확률이다.
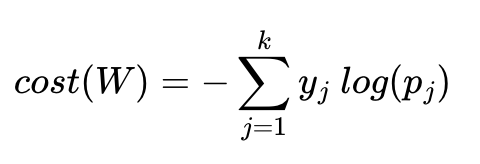
c가 실제값 원-핫 벡터에서 1을 가진 원소의 인덱스일 때 Pc = 1은 정확하게 예측한 경우이다.
이를 식에 대입해보면 -1log(1) = 0이고 정확하게 예측했을 때 크로스 엔트로피 함수의 값은 0임을 알 수 있다.
n개의 전체 데이터에 대한 평균을 구한다고 하면 최종 비용 함수는 다음과 같다.
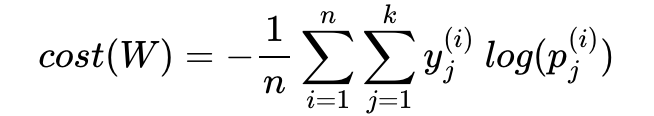
이진 분류에서의 크로스 엔트로피 함수
로지스틱 회귀의 가설식을 다시 보자.
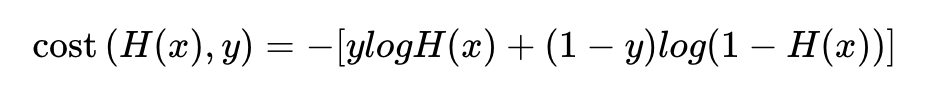
이 식에서 y를 y1, 1-y을 y2로 치환하고 H(x)을 p1, 1-H(X)를 p2로 치환하면
결과적으로 -(y1log(p1) + y2log(p2))이다
소프트맥스 함수의 최종 비용 함수에서 k = 2라고 가정하면 결국 로지스틱 회귀의 비용 함수와 같다.
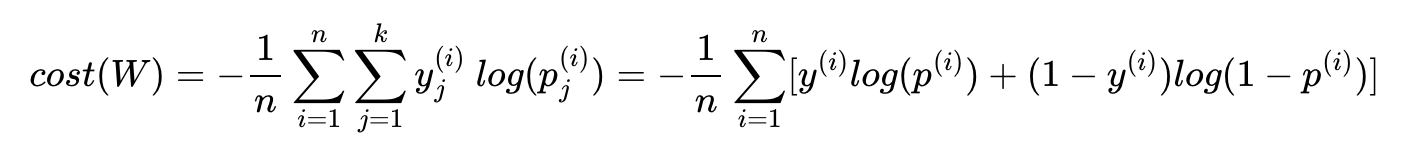
소프트맥스 회귀의 비용 함수 구현하기
3개의 원소를 가진 벡터 텐서를 정의하고, 이 텐서를 소프트맥스 함수의 입력으로 사용해보자.
z = torch.FloatTensor([1, 2, 3])
hypothesis = F.softmax(z, dim=0)
print(hypothesis) #tensor([0.0900, 0.2447, 0.6652])이번엔 비용 함수를 직접 구현하기 위해 임의의 3 × 5 행렬의 크기를 가진 텐서를 만들고
두번째 차원에 대해서 소프트맥스 함수를 적용해보자.
z = torch.rand(3, 5, requires_grad=True)
hypothesis = F.softmax(z, dim=1)
print(hypothesis)tensor([[0.2867, 0.1239, 0.1985, 0.1215, 0.2694],
[0.1604, 0.2631, 0.1976, 0.1873, 0.1916],
[0.2077, 0.2415, 0.2068, 0.2223, 0.1217]], grad_fn=<SoftmaxBackward0>)소프트맥스 함수의 출력값은 예측값이다. 즉, 위 텐서는 3개의 샘플에 대해서 5개의 클래스 중 어떤 클래스가 정답인지를 예측한 결과이다.
이제 각 샘플에 대해서 임의의 레이블을 만들고
y = torch.randint(5, (3,)).long()
print(y) #tensor([0, 2, 1])각 레이블에 대해서 원-핫 인코딩을 수행하자.
# 모든 원소가 0의 값을 가진 3 × 5 텐서 생성
y_one_hot = torch.zeros_like(hypothesis)
y_one_hot.scatter_(1, y.unsqueeze(1), 1)tensor([[0., 1., 0., 0., 0.],
[1., 0., 0., 0., 0.],
[0., 0., 1., 0., 0.]])이제 소프트맥스 회귀의 비용함수를 코드로 구현해보자.
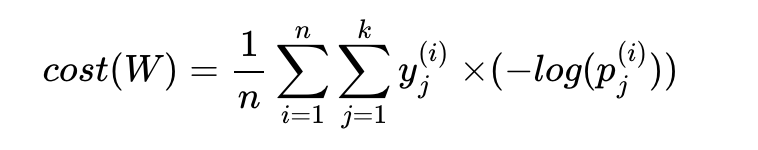
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
print(cost)그런데 위의 torch.log(F.softmax(z, dim=1))를 F.log_softmax()로 대체할 수도 있다.
# 두번째 수식
(y_one_hot * - F.log_softmax(z, dim=1)).sum(dim=1).mean()
# 또는
F.nll_loss(F.log_softmax(z, dim=1), y)
# 또는
F.cross_entropy(z, y)F.cross_entropy()는 F.log_softmax()와 F.nll_loss()를 포함한다.
소프트맥스 회귀 구현하기
훈련 데이터와 레이블을 텐서로 선언하자.
x_train의 각 샘플은 4개의 특성을 가지고 있으며, 총 8개의 샘플이 존재한다.
y_train은 각 샘플에 대한 레이블이고, 여기서는 0, 1, 2 즉 총 3개의 클래스가 존재한다.
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)x_train의 크기는 8 × 4이고 y_train의 크기는 8 × 1이다.
그런데 최종 사용할 레이블은 y_train에서 원-핫 인코딩을 한 결과여야 한다.
클래스의 개수는 3개이므로 y_train에 원-핫 인코딩한 결과는 8 × 3의 개수를 가져야 한다.
y_one_hot = torch.zeros(8, 3)
y_one_hot.scatter_(1, y_train.unsqueeze(1), 1)
print(y_one_hot.shape)y_train에서 원-핫 인코딩을 한 결과인 y_one_hot의 크기는 8 × 3이다.
즉, W 행렬의 크기는 4 × 3이어야 한다.
이제 W와 b를 선언하고, 옵티마이저로는 경사 하강법을, 학습률은 0.1로 설정하자.
# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros((1, 3), requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)F.softmax()와 torch.log()를 사용하여 가설과 비용 함수를 정의하고, 총 1,000번의 에포크를 수행하자.
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# 가설
hypothesis = F.softmax(x_train.matmul(W) + b, dim=1)
# 비용 함수
cost = (y_one_hot * -torch.log(hypothesis)).sum(dim=1).mean()
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))또는 F.cross_entropy()을 사용하여
# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros((1, 3), requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산
z = x_train.matmul(W) + b
cost = F.cross_entropy(z, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))
또는 nn.Module을 통해 구현해보자.
output_dim이 1이었던 선형 회귀때와 달리 여기서 output_dim은 클래스의 개수여야 한다.
# 모델을 선언 및 초기화. 4개의 특성을 가지고 3개의 클래스로 분류. input_dim=4, output_dim=3.
model = nn.Linear(4, 3)# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.cross_entropy(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))또는 클래스로 구현할 수도 있다.
class SoftmaxClassifierModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(4, 3) # Output이 3!
def forward(self, x):
return self.linear(x)
model = SoftmaxClassifierModel()
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.cross_entropy(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))소프트맥스 회귀로 MNIST 데이터 분류하기
http://yann.lecun.com/exdb/mnist
MNIST는 숫자 0부터 9까지의 이미지로 구성된 손글씨 데이터셋으로
총 60,000개의 훈련 데이터와 레이블,
총 10,000개의 테스트 데이터와 레이블로 구성되어있다.
(레이블은 0부터 9까지 총 10개)
각각의 이미지는 아래와 같이 28 픽셀 × 28 픽셀의 이미지이고 28 픽셀 × 28 픽셀 = 784 픽셀이므로, 각 이미지를 총 784의 원소(특성)를 가진 샘플이 된다.
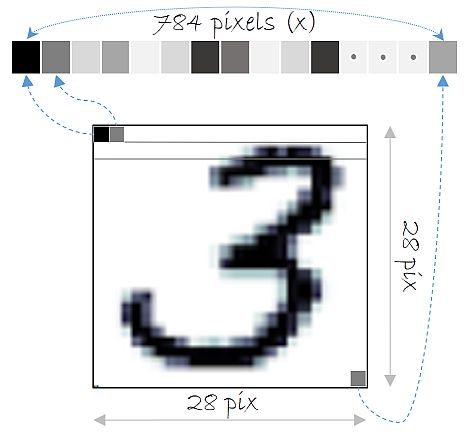
784차원의 벡터로 만드는 코드이다.
X는 for문에서 호출될 때는 (배치 크기 × 1 × 28 × 28)의 크기를 가지지만, view를 통해서 (배치 크기 × 784)의 크기로 변환된다.
for X, Y in data_loader:
# 입력 이미지를 [batch_size × 784]의 크기로 reshape
# 레이블은 원-핫 인코딩
X = X.view(-1, 28*28)MNIST 분류기 구현하기
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import matplotlib.pyplot as plt
import randomtorchvision은 유명한 데이터셋들, 이미 구현되어져 있는 유명한 모델들, 일반적인 이미지 전처리 도구들을 포함하고 있는 패키지이다.
현재 환경에서 GPU 연산이 가능하다면 GPU 연산을 하고, 그렇지 않다면 CPU 연산을 하도록 하자
USE_CUDA = torch.cuda.is_available() # GPU를 사용가능하면 True, 아니라면 False를 리턴
device = torch.device("cuda" if USE_CUDA else "cpu") # GPU 사용 가능하면 사용하고 아니면 CPU 사용
print("다음 기기로 학습합니다:", device)랜덤 시드를 고정하고 하이퍼파라미터를 변수로 두자.
# for reproducibility
random.seed(777)
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)
# hyperparameters
training_epochs = 15
batch_size = 100# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
mnist_test = dsets.MNIST(root='MNIST_data/',
train=False,
transform=transforms.ToTensor(),
download=True)root는 MNIST 데이터를 다운로드 받을 경로
train은 인자로 True를 주면, MNIST의 훈련 데이터를 리턴받으며 False를 주면 테스트 데이터를 리턴받는다.
transform은 현재 데이터를 파이토치 텐서로 변환한다는 뜻이며
download는 해당 경로에 MNIST 데이터가 없다면 다운로드 받겠다는 의미이다.
데이터를 다운받고 미니 배치와 데이터로드 챕터에서 학습했던 데이터로더(DataLoader)를 사용해보자.
# dataset loader
data_loader = DataLoader(dataset=mnist_train,
batch_size=batch_size, # 배치 크기는 100
shuffle=True,
drop_last=True)dataset은 로드할 대상을 의미하며, batch_size는 배치 크기, shuffle은 매 에포크마다 미니 배치를 셔플할 것인지의 여부, drop_last는 마지막 배치를 버릴 것인지를 의미한다.
이 때 drop_last는
1,000개의 데이터, 배치 크기가 128이라고 했을 때 1,000을 128로 나누면 총 7개가 나오고 나머지로 104개가 남는다.
이때 마지막 배치 104개를 버리기 위해 drop_last=True를 하는데
이는 다른 미니 배치보다 개수가 적은 마지막 배치를 경사 하강법에 사용하여 마지막 배치가 상대적으로 과대 평가되는 현상을 막아준다.
input_dim은 784이고, output_dim은 10인 모델을 설계하자.
# MNIST data image of shape 28 * 28 = 784
linear = nn.Linear(784, 10, bias=True).to(device)bias는 편향 b를 사용할 것인지를 나타내며 기본값은 True이다.
비용 함수와 옵티마이저를 정의하자.
비용 함수와 옵티마이저 정의
criterion = nn.CrossEntropyLoss().to(device) # 내부적으로 소프트맥스 함수를 포함하고 있음.
optimizer = torch.optim.SGD(linear.parameters(), lr=0.1)for epoch in range(training_epochs): # 앞서 training_epochs의 값은 15로 지정함.
avg_cost = 0
total_batch = len(data_loader)
for X, Y in data_loader:
# 배치 크기가 100이므로 아래의 연산에서 X는 (100, 784)의 텐서가 된다.
X = X.view(-1, 28 * 28).to(device)
# 레이블은 원-핫 인코딩이 된 상태가 아니라 0 ~ 9의 정수.
Y = Y.to(device)
optimizer.zero_grad()
hypothesis = linear(X)
cost = criterion(hypothesis, Y)
cost.backward()
optimizer.step()
avg_cost += cost / total_batch
print('Epoch:', '%04d' % (epoch + 1), 'cost =', '{:.9f}'.format(avg_cost))
print('Learning finished')# 테스트 데이터를 사용하여 모델을 테스트한다.
with torch.no_grad(): # torch.no_grad()를 하면 gradient 계산을 수행하지 않는다.
X_test = mnist_test.test_data.view(-1, 28 * 28).float().to(device)
Y_test = mnist_test.test_labels.to(device)
prediction = linear(X_test)
correct_prediction = torch.argmax(prediction, 1) == Y_test
accuracy = correct_prediction.float().mean()
print('Accuracy:', accuracy.item())
# MNIST 테스트 데이터에서 무작위로 하나를 뽑아서 예측을 해본다
r = random.randint(0, len(mnist_test) - 1)
X_single_data = mnist_test.test_data[r:r + 1].view(-1, 28 * 28).float().to(device)
Y_single_data = mnist_test.test_labels[r:r + 1].to(device)
print('Label: ', Y_single_data.item())
single_prediction = linear(X_single_data)
print('Prediction: ', torch.argmax(single_prediction, 1).item())
plt.imshow(mnist_test.test_data[r:r + 1].view(28, 28), cmap='Greys', interpolation='nearest')
plt.show()
