[Information Theory] KL divergence

KL Divergence

• Kullback-Leibler Divergence
• 두 확률 분포 간의 정보량의 차이를 측정하는 비대칭적인 척도
• 주어진 두 분포 P와 Q에서, P가 실제 분포이고 Q가 이를 근사하는 분포일 때 KL Divergence는 Q가 P를 얼마나 잘 설명하는지를 나타냄

공식

기본적인 정의: $D_{KL}(P || Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}$
이를 직관적으로 이해하기 위해 다음과 같이 변형해보자.

로그의 성질을 이용해 로그의 차이로 변형하면 $\sum_{x} P(x) (\log P(x) - \log Q(x))$
위의 식에서 재배열하여 $-\sum_{x} P(x) (\log Q(x) - \log P(x))$

이를 두개의 항으로 분리하면 $-\sum_{x} P(x) \log Q(x) - \left(-\sum_{x} P(x) \log P(x)\right)$

이렇게 보면 KL Divergence는 cross-entropy에서 entropy를 뺀 값이 된다.

이는 cross-entropy에서 기준 분포 p(x)의 entropy를 빼줌으로써
-> 즉 두 분포 사이 차이에서 기준 분포 자체의 불확실성을 제거함으로써
두 분포가 얼마나 서로 다른 정보를 가지고 있는지를 순수하게 측정하는 방법이다.

예시

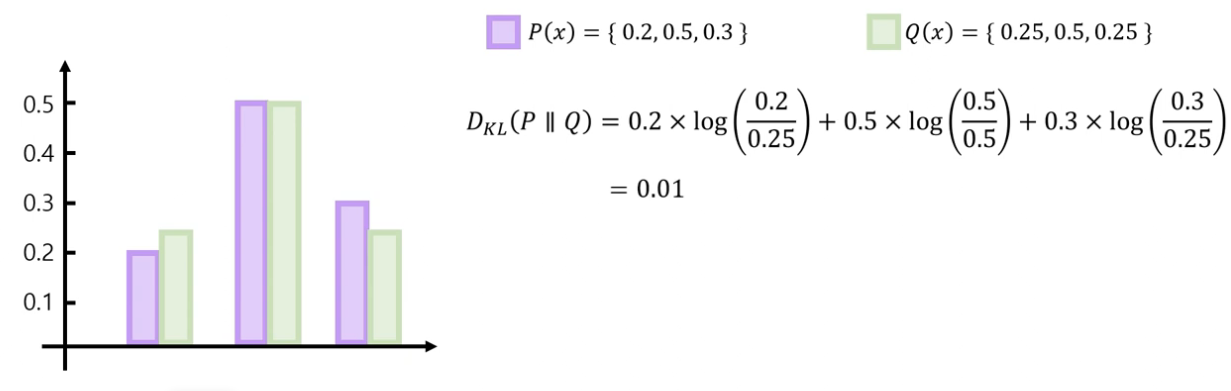
위 두가지 예시에서 알 수 있듯, 두 분포 P(x), Q(x)가 유사하면 KL Divergence는 작아진다.

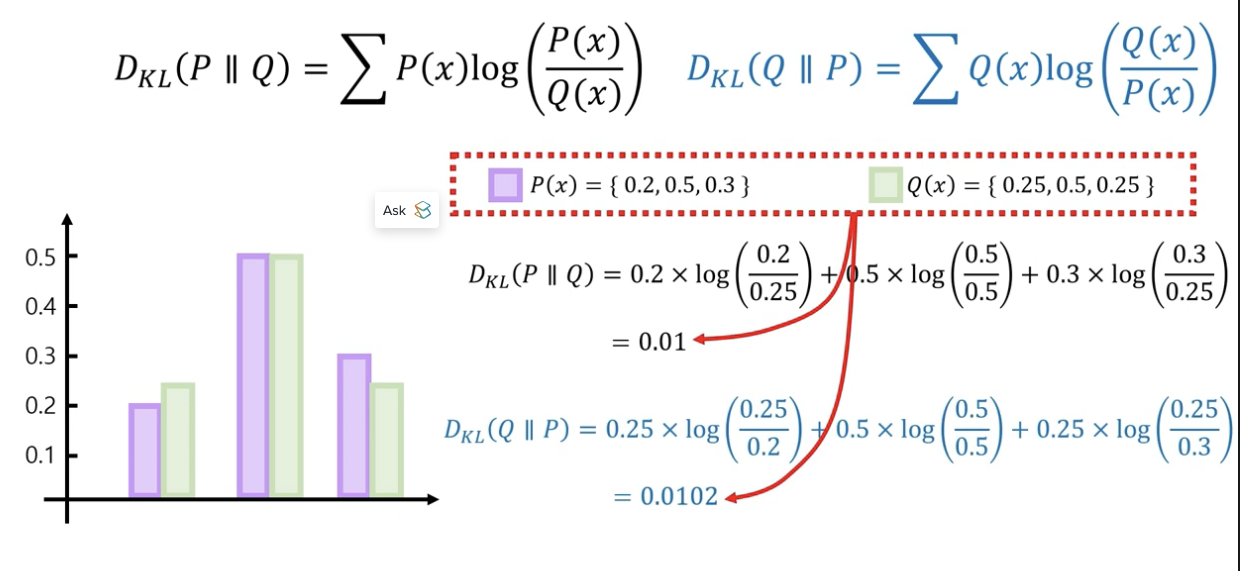
또 KL Divergence는 비대칭으로, 위와 같이 기준 분포가 바뀔 경우
같은 분포를 사용하여도 KL Divergence의 값은 달라진다.

단점

• 위의 경우와 같이 비대칭성의 문제로 인해 두 분포의 차이를 계산할 때 기준 분포를 고려해야 하고
• KL Divergence의 값의 범위는 0부터 무한대까지 나올 수 있으므로 모델을 업데이트 할 때 문제가 발생할 수 있다.
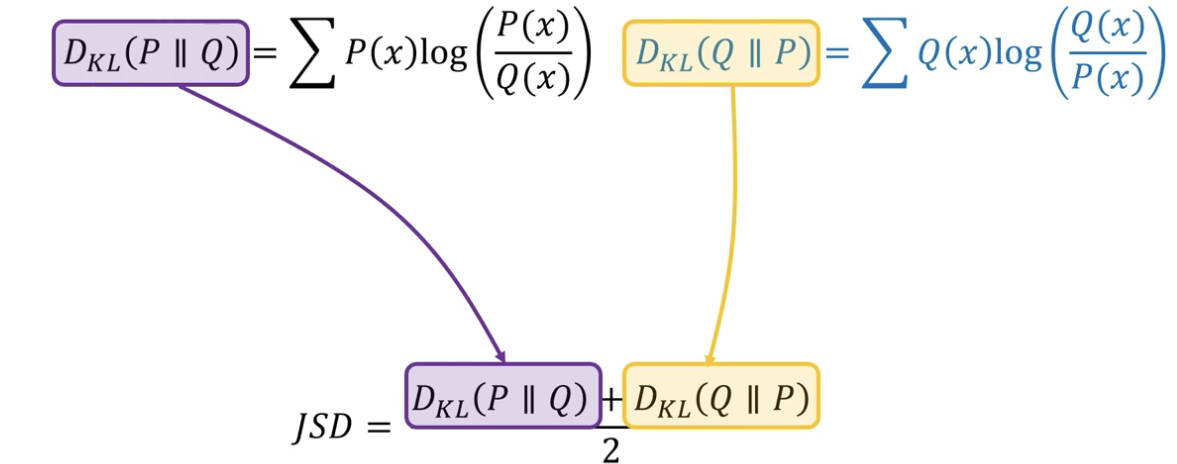
• 그래서 이를 보완한 방법으로 Jensen-Shannon Divergence (JSD)가 있는데, 두 분포가 만드는 KL divergence의 값들을 합해 2로 나눈 값이다.
  

신박AI
초보를 위한 정보이론 안내서 - KL divergence 쉽게 보기
[정보이론] KL-divergence