[Information Theory] Entropy, Cross Entropy

확률, 놀람, 정보

• 확률이 높으면 그 사건이 발생했을 때 별로 놀라지않고. 확률이 낮으면 그 사건이 발생했을 때 놀라게 된다
• 즉 확률과 놀람은 서로 반비례의 개념이다.
• 놀람을 수학적으로 표현하자면, 확률이 p(x)이면 놀람은 1/p(x)
• 정보이론에서 놀람의 공식은 log(1/p(x))
• 그런데 정보이론에서는 놀람이라는 표현보단 정보라는 단어를 사용하고,
• 정보란, 의외성 또는 놀람을 객관적인 수치로 표현한 것
• $log(\frac{1}{p(x)}) = log(1) - log(p(x))$
• $= 0 - log(p(x)) = -log(p(x))$

기댓값

• 어떤 값에 확률을 곱한 값
• $\mathbb{E}[X] = \sum_{x} x \cdot P(x)$

엔트로피

• measure of uncertainty(불확실성의 척도), 놀람의 예상값

• 기댓값 공식의 x 대신에 놀람을 넣으면 됨

• $H(X) = \sum log(\frac{1}{p(x)}) \cdot P(x)$

• 높은 엔트로피는 불확실성이 높고, 낮은 엔트로피는 불확실성이 낮다

• 동전을 던졌을 때/주사위를 던졌을 때 중에서 불확실성(어떤 데이터가 나올지 예측하기 어려운 것)은 주사위가 더 크다.(무엇이 나올지 알기 어려운 주사위의 경우가 엔트로피가 더 높은 것)

• 동전이 앞면이 나올지, 뒷면이 나올지는 머신러닝의 binary classification 문제와 동일함(두개 중 하나)

크로스 엔트로피

• y가 연속형이 아니라 범주형일 경우(분류) MSE 같은 비용함수는 의미가 없고, 크로스엔트로피를 사용함

• 크로스엔트로피는 p(x)의 확률에 q(x)의 놀람도를 곱함

• $H(P,Q) = \sum log(\frac{1}{q(x)}) \cdot P(x)$

• ex)배민에서 평점을 보고 치킨을 시켰는데, 막상 먹어보니 별로더라

• 즉 평점(확률)과 내가 겪은 현실(놀람)과의 차이가 존재할 때

• 이를 크로스엔트로피 손실과 같은 경우이다.

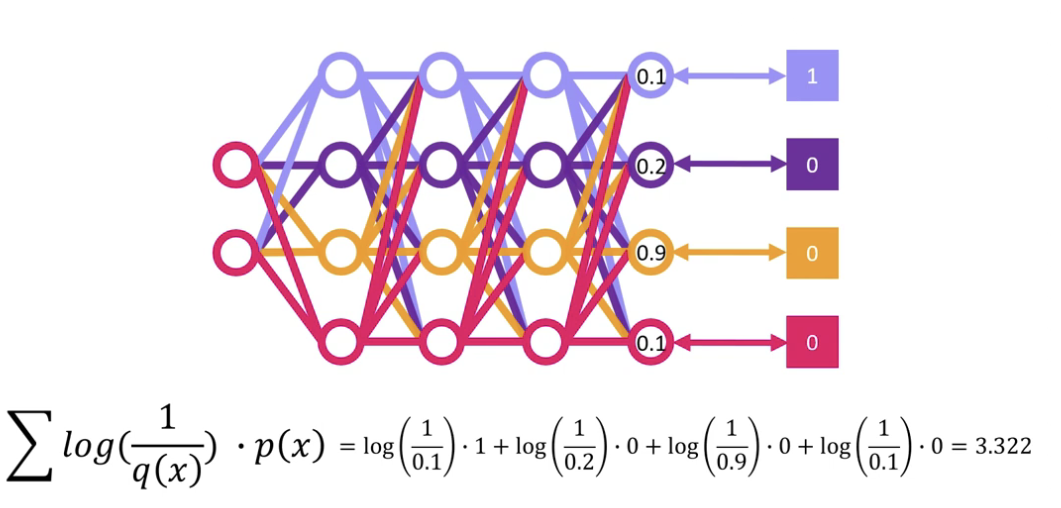
• 이 loss가 작아지는 방향으로 신경망의 가중치들을 업데이트하여
• 신경망의 아웃풋이 업데이트되며 실제값과 가까워지면

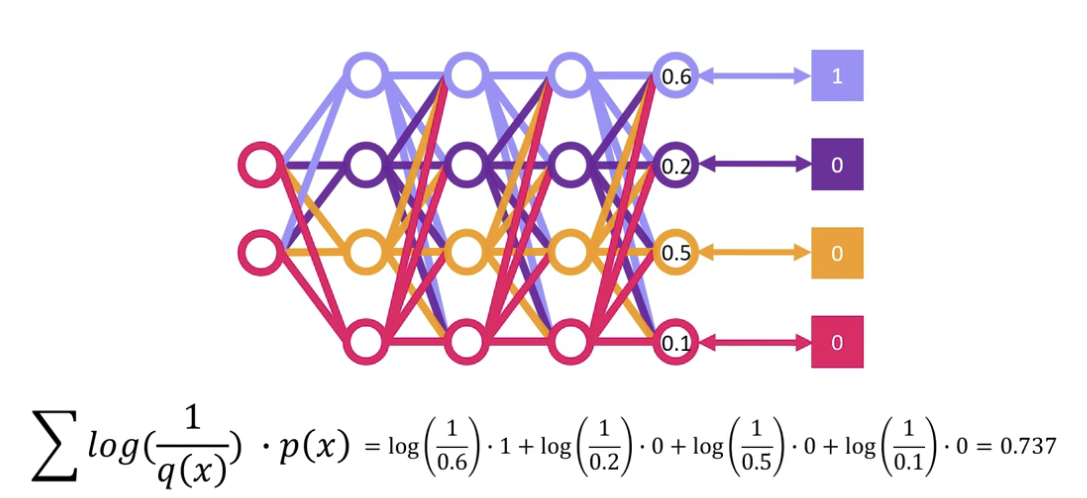
• 크로스엔트로피 손실도 줄어든다.

MSE VS CEL

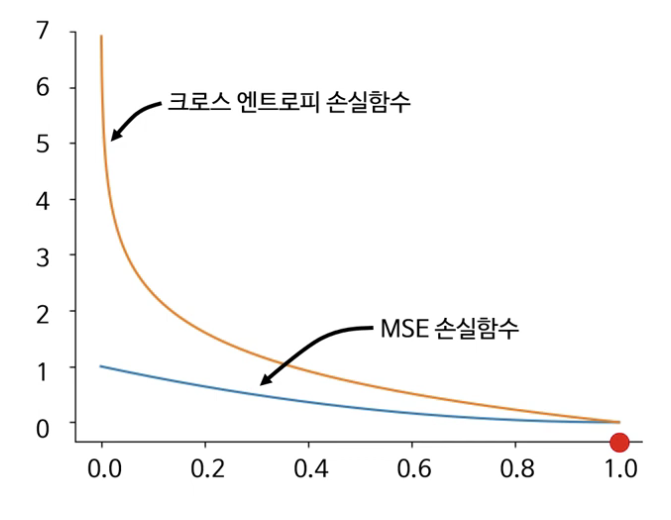
• 예측값이 떨어질 수록 크로스 엔트로피의 손실값과 기울기가 MSE보다 커서
• 예측값이 실제값에 비해 멀 수록 크로스엔트로피가 MSE에 비해 효율적으로 손실을 최소화할 수 있음

Reference

‍김성범[ 교수 / 산업경영공학부 ]

신박AI

초보를 위한 정보이론 안내서 - Entropy란 무엇일까

Cross-entropy 의 이해: 정보이론과의 관계

혁펜하임 정보이론 기초 15분 컷!