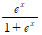참고:
퀀트 투자를 위한 머신러닝, 딥러닝 알고리즘 트레이딩
https://ko.wikipedia.org/wiki/%EB%A1%9C%EC%A7%80%EC%8A%A4%ED%8B%B1_%ED%9A%8C%EA%B7%80
데이터 포인트를 범주 혹은 클래스에 할당하는 모델. 관측치를 분류한다라고 표현한다.
다양한 분류 기법과 분류기가 있는데, 우선은 로지스틱 회귀 분석(logistic regression)만 정리한다. 나머지는 책의 뒷장에 나온다고 한다.
로지스틱 회귀 분석 또한 다른 회귀분석과 마찬가지로 종속 변수와 독립 변수간의 관계를 구체적인 함수로 나타내는 것이 목표이다. 일반 선형 회귀처럼 독립 변수의 선형 결합으로 종속 변수를 설명하지만, 종속 변수가 범주형 데이터(카테고리)를 대상을 대상으로 하며 데이터의 결과가 분류로 나뉘기 때문에 분류 기법으로도 볼 수 있다. 보통 유효한 범주가 2개일 때 주로 사용되지만, 3개짜리로도 쉽게(양 끝 이상은 0혹은 2, 중간은 1) 확장해서 사용할 수 있다. 카테고리가 더 많을 수도 있다.
선형회귀와의 주된 차이점은 일단 종속 변수(y)가 [0,1]의 범위로 제한된다는 점, 그리고 종속 변수가 이진적이므로 조건부확률의 분포가 정규분포 대신 이항 분포를 따른다는 점이다.
가장 많이 쓰이는 모델은 로지스틱 모형으로 아래 식과 같다.
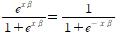
이 식이 p(x)이다. odds 식(p/(1-p))에 이 값을 대입하고 log을 씌우면 이것이 로짓 변환이며, 다음 관계가 성립한다.
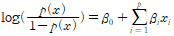
모델의 fit로는 MSE대신 MLE(최대 우도 추정)를 사용한다. 주가가 오르는 모든 경우에 대해 1을 내고 그렇지 않으면 0에 가까운 수치를 내도록 하는 것이다.
따라서 목표는 다음 값을 최대화 하는 beta들의 조합을 찾는 것이 된다.
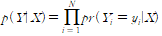
로그를 씌운뒤, 방정식을 최대화하기 위한 식을 세우면
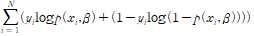
의 beta에 대한 미분값이 0이 되면 된다.
모델이 항상 수렴하는 것은 아니다. 닫힌 형태를 바로 구하는 것이 불가능해, 반복 처리를 통해 수렴 여부를 확인하는데 이 경우 계수가 중요한 의미를 갖지 않는 것을 의미한다. 모델이 실패하는 대표적인 이유들은 사건에 매우 큰 영향을 끼치는 예측 변수의 사용, 다중 공선성, 희소성(sparseness : 전체 공간에 비해 데이터가 있는 공간이 매우 협소), 완분성(complete separation : 특정 독립변수에 의해 종속 변수가 완전히 설명히 됨.)
선형 회귀와 마찬가지로 크기에 민감하기 때문에 입력 변수를 표준화 해놓고 모델을 적용해야 한다.
파이썬으로는
import statsmodels.api as sm
model= sm.Logit(data.target, sm.add_constant(data.drop('target',axis=1)))
result=model.fit()
result.summary()처럼 사용한다.
출력된 결과에서 LL-null는 독립변수 없이 intercept만 있었을 때의 log likelihood를 의미한다. Log-likelihood는 독립변수가 추가되었을 때의 최대우도이므로, Ll-null보다는 큰 값이 나올 것을 예상하게 된다.
또한 결과에서 나오는 값은 pseudo R2이다. 가장 많이 쓰이는 것은 pseudo R2(Mcfadden R2), Cox and Snell R2, Nagelkerke R2이렇게 세 가지라고 한다.
https://ukchanoh.wordpress.com/2015/02/17/r2logistic/
이 글에서 정리 된 것을 그대로 정리해서 옮겨 놓았다.
모델을 수정할 때는 모델을 더욱 복잡하게 만들거나, 추가적인 비선형항 혹은 상호작용항이 필요한지 검증 후 수정하는 것들이 적용된다.
이후 fit여부를 확인할 때 여러 R2중에 하나를 쓰는데, 어떤것이 최선인지에 대한 구체적인 합의는 없다.
우선 psdeudo R2의 식은 R2McF = 1 – ln(LM) / ln(L0) 이다. L0가 ll-null에 해당하는 값이다. 이 값이 선형회귀 분석에서 RSS와 동일한 역할을 해 준다.
C&S R2의 식은 다음과 같다. R2C&S = 1 – (L0 / LM)^(2/n) 문제는 이 값은 최대값이 1 보다 반드시 작다는 것이다. 1 – L0^(2/n)(LM=1)이 최대값이 된다. 발생확률이 0.5일때 최대 0.75이며 치우친 경우에는 최대값이 훨씬 작아지게 된다.
Nagelkerke R2는 위에 대한 개선으로, 나온 값을 최대값으로 나눠주는 것이다. 그러면 발생확률에 따라 다른 값을 나눠주게 되는데 이 과정에서 이론적 장점이 크게 훼손된다. 또한 일반 선형 모델에서 나오는 값보다 일반적으로 큰 값을 보인다.
Tjur R2는 꽤 다른 접근으로, 종속 변수의 두 범주 각각의 예측확률의 평균값을 계산하고 그 차이값을 구한다. (사건이 발생한 사례에 높은 예측값, 아닌 것에 낮은 예측값이 나오는 것이 최선의 상황.) 상한이 1이며, R2정의와 밀접히 관련되고, 계산도 쉽다.
Tjur 를 반대할 만한 이유로 최우함수의 수치에 기반하지 않는 방식이라는 것이다. 그래서 복잡성이 증가해도 R2는 줄어들 수 있다. 또한 일반화가 어렵다는 단점도 있다.
다시 돌아가서, llr p-value값에 따라 귀무가설을 기각할 수 있다.
from sklearn.metrics import roc_auc_score
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
이를 이용해도 LogisticRegression을 할 수 있다.