참고:
퀀트 투자를 위한 머신러닝, 딥러닝 알고리즘 트레이딩
https://datascienceschool.net/03%20machine%20learning/04.02%20%EC%84%A0%ED%98%95%ED%9A%8C%EA%B7%80%EB%B6%84%EC%84%9D%EC%9D%98%20%EA%B8%B0%EC%B4%88.html
선형 회귀 모델은 출력이 입력의 선형 결합이라고 가정. 이 모델에는 데이터가 예측값을 벗어나는데 대한 확률오차가 있다고 가정한다. 모델이 데이터를 완전히 설명하지 못 하는 이유로는 변수의 누락, 측정 오차, 데이터 수집 이슈 등이 포함된다.
표본을 이용해 모집단의 실제 관계에 대한 결론을 이끌려면, 오차에 대한 추가 가정이 필요하다. 이 가정은 '독립적이고 동일하게 분포된 오차' 이며, 이로 인해 공분산 행렬을 만들면 I가 된다. 이 가정이 성립하면 OLS(ordinary least squares) 방법이 편향도 없으며 효율적인 추정치를 제공한다는 것을 보장한다. 당연하지만, 잘 성립하지 않는다. 횡단면, 혹은 시간 경과에 따른 노출을 보는 것은 당연히 시간 또는 횡단면 차원의 상관관계를 나타내므로 공분산 행렬이 I가 아니게 되고, 이를 이용하는 알고리즘들이 있다.
선형 모델에서 파라미터를 학습할 때, shrinkage를 적용하여 패널티항을 적용하는 regularization을 통해 복잡성을 감소시키기도 한다.
가장 기본은 다중 선형 모델이다.
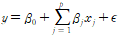
각 계수는 다른 모든 변수가 일정할 때, 해당 변수가 변할 때 평균적으로 변하는 정도를 나타낸다. 벡터를 이용해 표현할 수도 있는데 이경우 y = Xb+E 로, y는 N X 1, X = N X P, b는 P X 1, e도 N X 1짜리 가 된다.
선형 모델이지만 꼭 모든 파라미터를 선형으로 사용하는 대신 로그항을 넣은 다던지, 더미 인코딩을 사용한다던지 등의 방법을 적용할 수 있다.
파라미터를 훈련시키는 방법 중 몇 가지는 최소 자승법(OLS, ordinary least squares), 최대 우도 추정(maximum likelihood estimation), 확률적 경사 하강법(Stochastic gradient descent)가 있다.
OLS: OLS는 잔차의 제곱(RSS, residual sum of squares)을 전부 합한 값이 최소가 되도록 하는 beta값들의 쌍을 결정하는 것이다.
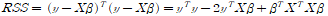
이므로, RSS값을 최소로 하기 위해 beta에 대해 이를 미분하면
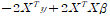
가 0이 되어야 하므로,
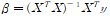
가 된다.
문제는 이렇게 해를 구하려면 X^TX가 역행렬이 존재해야 된다는 점이다. 즉, X의 각 행 혹은 열이 독립적이어야 된다. 그게 아니면 다른 방식을 사용해야 한다.
위 식에 대해 또 다른 해석도 가능하다. 0이 되는 식을 보면
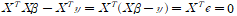
이다. 즉 데이터가 속한 모든 차원의 하위 공간에 대해 잔차 벡터가 직교가 되는 계수가 RSS를 최소화 하는 계수가 되는 것이다.
파이썬에서는 간단하게 사용할 수 있다. 물론, np.linalg.inv(), .dot등을 이용해 직접 계산식을 만들어 내서 계수를 계산할 수도 있다.
import statsmodels.api as sm
X_ols = sm.add_constant(X)
model = sm.OLS(y, X_ols).fit()
print(model.summary())
혹은
from sklearn.linearmodel import LinearRegression
model = LinearRegression().fit(X, y)
print(model.intercept, model.coef_)
도 선형회귀 모델이다.
다중 변수 모델의 경우
model = sm.OLS.from_formula("y ~ x", data=df)
result = model.fit()
처럼 생성한다.
파이썬에서 이 코드를 실행했을 때 결과들의 해석은 아래와 같다.
계수의 p value : 각각 값이 0이라는 귀무가설에 대한 검정 값이다. 특정 임계값보다 작으면 유의하다.
f value : 모델 전체에 대해 유의한지를 보는 검정 값.
dw: serial correlation
omnibus, jaarque-bera : 잔차가 정규분포라는 귀무가설.
conditional number: 다중 공선성에 대한 값. 30을 초과하는 값을 가지면 유의한 다중 공산성을 가질 수 있다는 것을 의미한다.
MLE(maximum likelihood estimation) : 최대 우도 추정법
https://angeloyeo.github.io/2020/07/17/MLE.html
위 블로그에 굉장히 잘 정리되어 있었다. 글을 따라 옮기면서 공부해 보았다.
요약을 해보면, 주어진 데이터를 바탕으로, 모델의 파라미터를 추정하는 방법이다.
likelihood(우도): 해당 데이터가 이 분포에서 나왔을 가능성. 이 값을 계산 하기 위해, 각 데이터 샘플이 후보 분포에 대한 높이를 계산해서, 이를 다 곱해준다. 특이한건 더해주는 대신 전부 곱해준다는 것이다. 그래서 보통 자연로그를 이용해, 로그 값들을 전부 더해준 log-likelihood function을 이용한다고 한다.
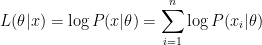
최대값을 찾기 위해서는 가장 보편적인 미분계수=0을 이용한다. L(세타|x)가 x및 세타에 대한 함수므로, 편미분을 이용해서 세타에 대해 미분해 준다.
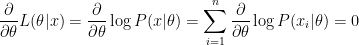
이게 되는 값들을 찾는다.
가정하는 모델이 정규분포라면, 계산결과를 보면 그냥 데이터의 평균 및 분산을 그대로 사용하면 된다는 편리함이 있다. 하지만 다른 모델을 가정하면 우도 값을 계산해서 최소화 해야 한다.
불편해 보이지만, 일반적인 경우에는 OLS를 적용할 수 없으므로 이 방법이 일반적인 데이터에 대한 추정 방법이 된다.
아마 모델에 따라 코드가 많이 달라져야 돼서 그런지, 딱 한번에 모든게 돌아가는 파이썬 코드는 없는 듯하다. 나중에 찾으면 갱신할 예정.
Gradient Descent는, 부드러운(연속?) 함수의 정지점을 찾는 범용 최적화 알고리즘이다. 예측 오차의 비용을 최소화할 때, 데이터를 이용해 현재 파라미터값에 대한 기울기를 계산한뒤, 그 값에 따라 파라미터를 수정한다. 결과적으로 파라미터는 해에 가깝게 이동하게 된다.
문제는 기울기가 주어졌을 때 얼마만큼 파라미터를 조정해야 하는가가 된다. 이 크기를 learning rate(학습률)이라고 한다. 데이터의 크기에 따라, 이 알고리즘을 전체 데이터에 대해 몇번 반복하는가를 에폭epoch이라고 한다.
이 알고리즘에 대한 무척 다양한 확장판이 있고, 잘 알려진 것은 확률적 경사 하강법(SGD, Sotchastic Gradient Desecent)이라고 한다. 기본 gradient descent의 단점인, global minima 대신 local minima에 빠지는 문제를 상당히 해결해 준다. 대충 요약하면 loss function을 전체 데이터를 이용하는 대신 부분(mini-batch)를 이용해서 계산하는 방식이다. 이와 다르게 BGD(Batch gradient desecent)는 전체 데이터를 이용한다.
선형 모델에 대해서 성립해야 되는 가정들을 정리한게 가우스-마르코프 정리다.(GMT, gauss-markov theorem)
- 모집단에서, 모형은 모수에 대해 선형을 유지한다.
- 각 데이터는 모집단에서 추출한 확률 변수이다.
- 입력 변수 사이에 정확한 선형관계는 없다. 즉 perfect collinearity가 성립하지 않는다. 이 경우 데이터의 오차항 끼리의 공분산의 기대값이 0이라는 뜻이기도 하다.
- 오차는 모든 입력에 대해 기대값이 0이다.
- 오차항은 입력 값에 상관 없이 동일 분산을 가진다.
이 가정하에, OLS는 불편(편향되지 않은) 추정치를 제공하게 된다. 또한, 표본 크기가 증가할 수록 추정치가 실제 값으로 가까워진다. 문제는 변수를 놓치거나, 형식이 달라지는 경우 모든 추정치가 편향된다는 결과 또한 발생한다는 것이다.
5번 항목이 꽤 중요한데, 이 가정을 추가하면 OLS를 이용해 BLUE(best linear unbiased estimator)를 산출한다. 즉, 가장 분산이 작은 계수들이 나온다는 것이다.
여기에 대해, 전통적으로 선형 모델은 정규성을 가정하는데, 이 가정은 실패할 때가 많다. 예를 들어 수익률은 전형적으로 정규분포가 아닌 사례다. 다만 정규성을 유지한다고 가정했을 때의 검정 통계량(pvalue)는 정규성이 아닐 때도 유효하기 때문에 유용하다.
t test로는 계수에 대한 가설 검정의 유의성을, f test로는 전체 회귀가 유의한지를 포함한 여러 모수에 대한 제한 검정을 확인한다.
이에 더해 라그라주 승수 검정응로 다중 제약을 테스트 한다.(f test의 대안)
모델이 잘 만들었는지 확인하는 적합도는 R2, 수정 R2, AIC, BIC 등이다. 뒤의 3가지는 모델이 복잡하면 패널티를 부여한다.
GMT의 모든 항이 다 지켜지는 경우면 좋겠지만, 그렇지 않은 경우도 많다. 그럼에도 항목이 위반되었을 때 그에 맞는 조정 방법도 존재한다.
5번의 경우, 평균에서 머리가 먼 입력값에서 오차가 커지는 경우가 있다.이 경우 t통계가 커져 false discovery(실제로는 기각하면 안 되지만 기각)가 될 수 있다. 이를 검증하는 두 가지가 BPtest(breusch pagan)과 white 검증이다. 두 가지 방법으로 이를 교정한다.
1. white standard errror를 사용해 이 분산성을 고려한다.
2. 표준오차를 클러스터링 해서, 그룹별로 모델을 생성한다.
그리고 OLS대신 사용하는 것으로 WLS, GLSAR, GLS가 있다.
4번의 위반은 serial correlation이다. 표준오차가 작아지고 마찬가지로 t 통계량이 커져 false discovery가 발생한다. DW-test로 이를 확인하고, 0~4의 값중 2에 가까울 수록 serial correlation이 없다는 의미가 된다.
3번의 위반은 multicollinearity(다중 공산성)이다. 개별 p값이 잘못 나올 수 있으며, 모델에 복합적인 영향을 끼친다. 이를 교정하는 공식적인 방법 혹은 이론적인 해결책은 없다. 이 경우는 관련 변수 하나 이상을 제거함으로써 교정한다.
scaler = StandardScaler()
X = scaler.fit_transform(X)
sgd = SGDRegressor(loss='squared_loss',
fit_intercept=True,
shuffle=True,
random_state=42,
learning_rate='invscaling',
eta0=0.01,
power_t=0.25)
sgd.fit(X=X, y=y)
coeffs = (sgd.coef * scaler.scale) + scaler.mean_
를 통해 SGD Regress 또한 가능하다. 이 모델은 normalize를 반드시 해 줘야 한다. 기울기가 규모에 민감하기 때문.
