작성자: 김상현

0. Node Embedding

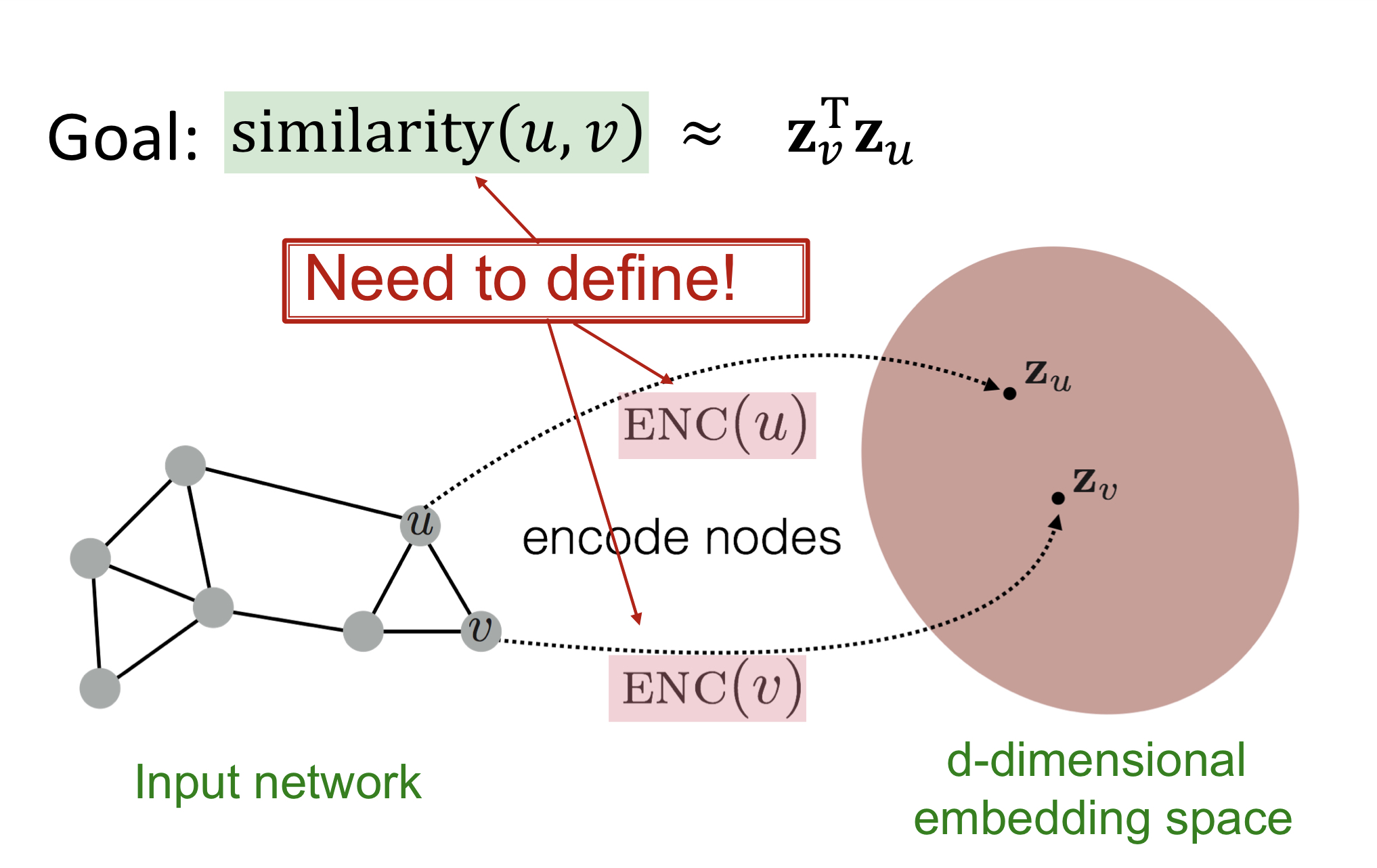
Node embedding은 graph의 node를 embedding space로 사상하는 encoder(ENC($\cdot$))를 찾는 과정이다. 이때, similarity($u,v$) $\simeq$ $z_v^T$$z_u$ 을 목표로 한다.

Shallow Encoders

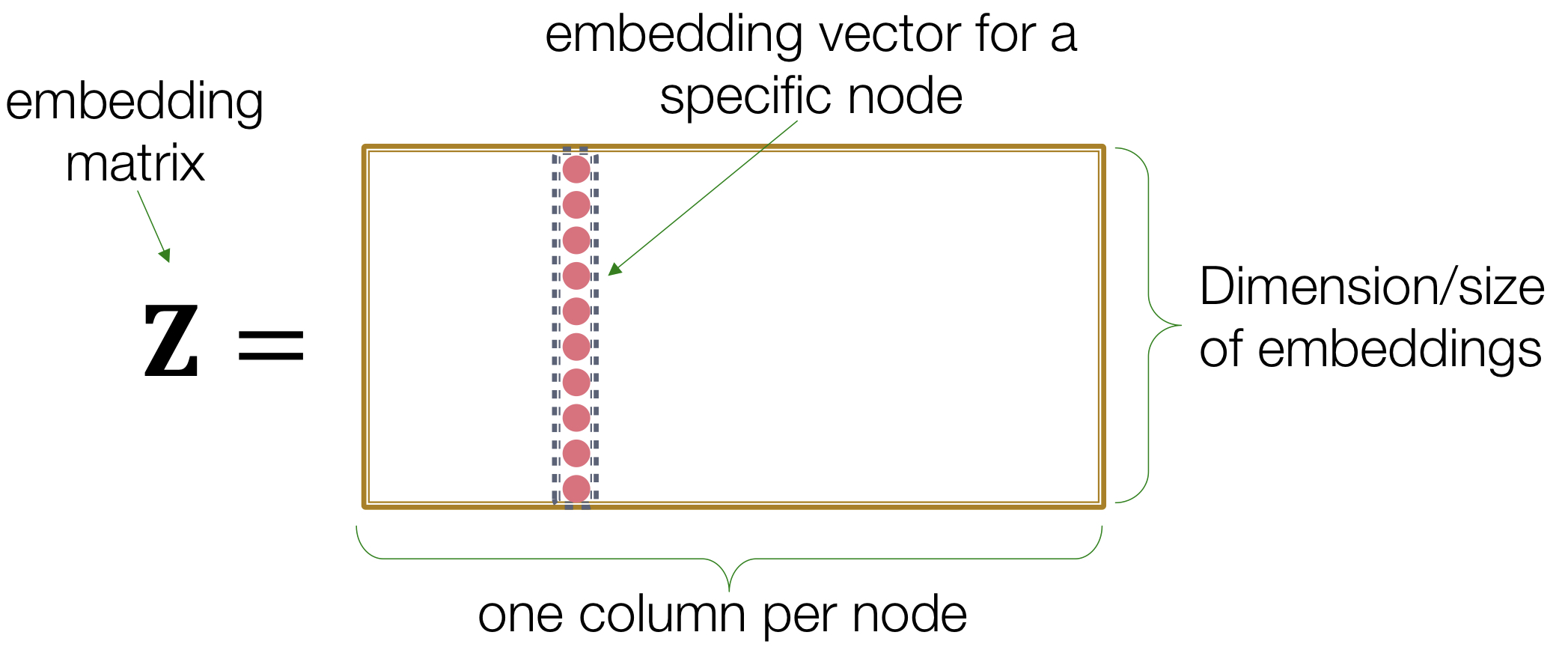
인코딩 방법으로 위 그림 같은 간단한 embedding-lookup 방법이 있다.

이 같은 방법에는 다음과 같은 한계(limitations)이 존재한다.

1. $O(|V|)$ parameters are needed
   • 노드 개수에 비례하는 parameters가 필요
2. Inherently "transductive"
   • 학습시 보지 못한 노드는 embedding 불가
3. Do not incorporate node features
   • 노드의 특징(features)를 고려하지 못함

---

Deep Graph Encoders

Shallow Encoders의 한계를 극복하기 위한 Graph Neural Network(GNN) 기반의 Deep Encoders 고려

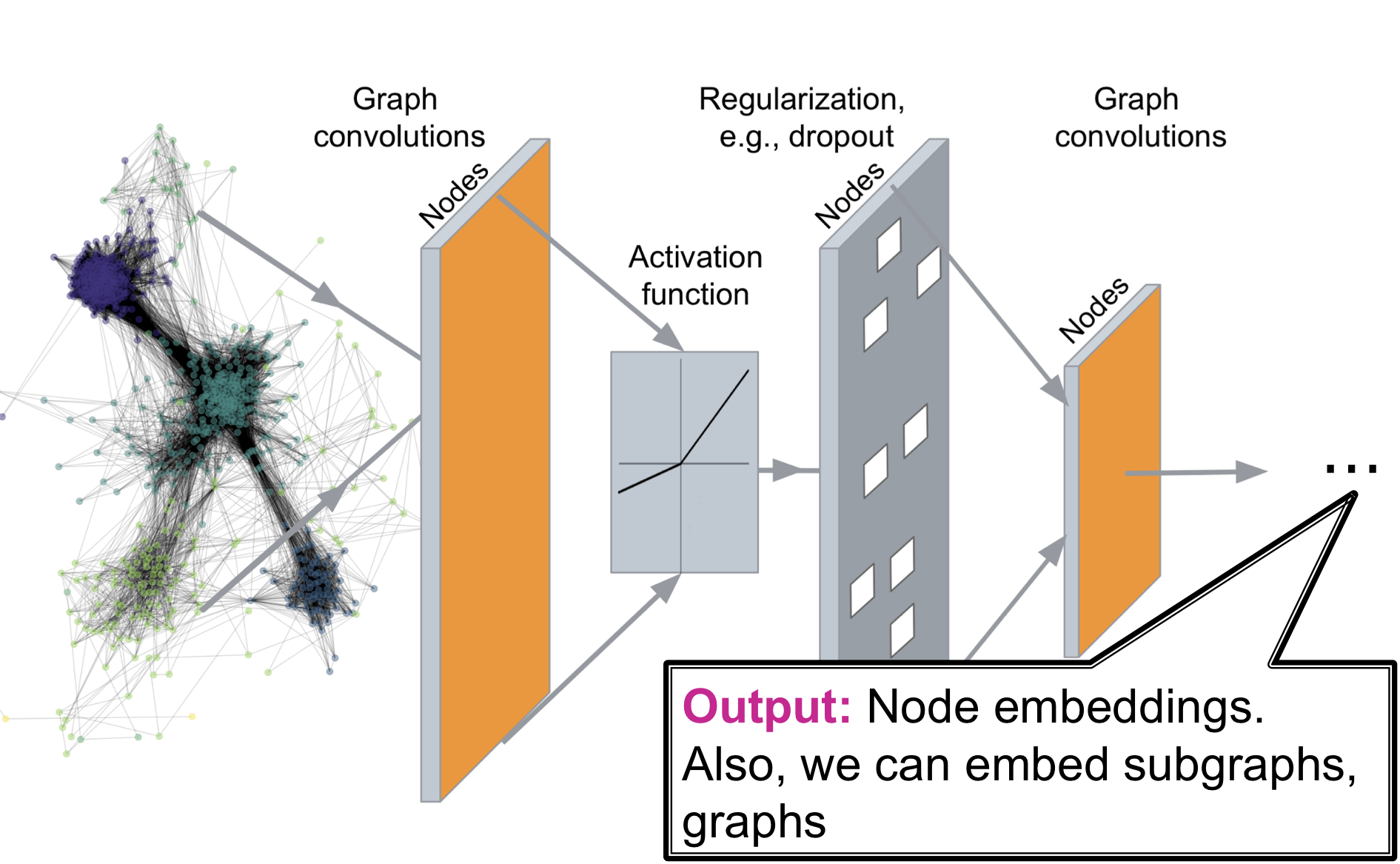
Deep Graph Encoders는 위 그림과 같이 임의의 graph를 Deep Neural Network를 통과시켜 우리가 원하는 embedding space로 사상시키는 것

---

1. Basics of Deep Learning

Machine Learning as Optimization

Supervised learning: 주어진 입력 $x$으로 범주 $y$ 예측을 목표

입력 $x$ 예시

• vectors of real numbers
• Sequences (natural language)
• Matrices (images)
• Graphs (potentially with node and edge features)

Supervised learning을 최적화 문제(optimization problem)로 공식화하면 다음과 같다.

$\Theta$: a set of parameters we optimize
$L(y,f(x))$: Objective function (=loss function)

참고) loss function의 종류: L2 loss, L1 loss, cross entropy, huber loss, hinge loss,...

---

Gradient Descent

최적화 문제를 해결하기 위해 경사하강법을 사용한다.

$\nabla_{\Theta}L$: gradient (기울기)
$\eta$: learning rate (학습률)

수렴할때(=종료조건)까지 반복적으로 gradient의 반대 방향으로 가중치를 업데이트

gradient란?
가장 크게 증가하는 방향으로의 방향 도함수
$\nabla_{\Theta}L = (\frac{\partial L}{\partial \Theta_{1}},\frac{\partial L}{\partial \Theta_{2}},...)$

Gradient Descent는 한번 가중치 업데이트시 모든 데이터를 사용해야 되는 단점이 존재한다. 이를 해결하기 위해 Stochastic gradient descent(SGD)를 사용한다

Stochastic gradient descent

• 경사하강법 수행할 때, 매 업데이트 마다 입력 데이터 $x$ 의 부분 집합인 mini batch를 이용해 가중치 업데이트
• SGD를 통한 gradient는 전체 gradient의 불편추정량 -> 하지만 수렴의 정도를 보장하지는 않는다.
• SGD를 개선한 optimizer 종류: Adam, Adagrad, Adadelta, RMSprop, ...

---

Multi-layer Perceptron

신경망(Neural network)은 linear transformation과 non-lineariy의 결합으로 이루어진 layer들이 쌓여진 형태이고, 이를 multi-layer perceptron이라 한다.

다층 구조의 학습을 위해 back-propagation 알고리즘을 이용하고, 비선형성을 위해 비선형함수 (e.g. sigmoid, ReLU,...)를 각 층마다 활성화 함수로 사용한다.

---

2. Deep Learning for Graphs

Setup

• $V$: vertex set
• $A$: adjacency matrix
• $X \in$ $R^{m \times |V|}$: matrix of node features
• $v$: a node in $V$
• $N(v)$: the set of neighbors of $v$

Node features

• Social networks: 사용자 정보, 사용자 사진
• Biological networks: 세포 정보
• 특별한 node feature가 없는 경우: node degree, one-hot vector 등등

Naive Approach

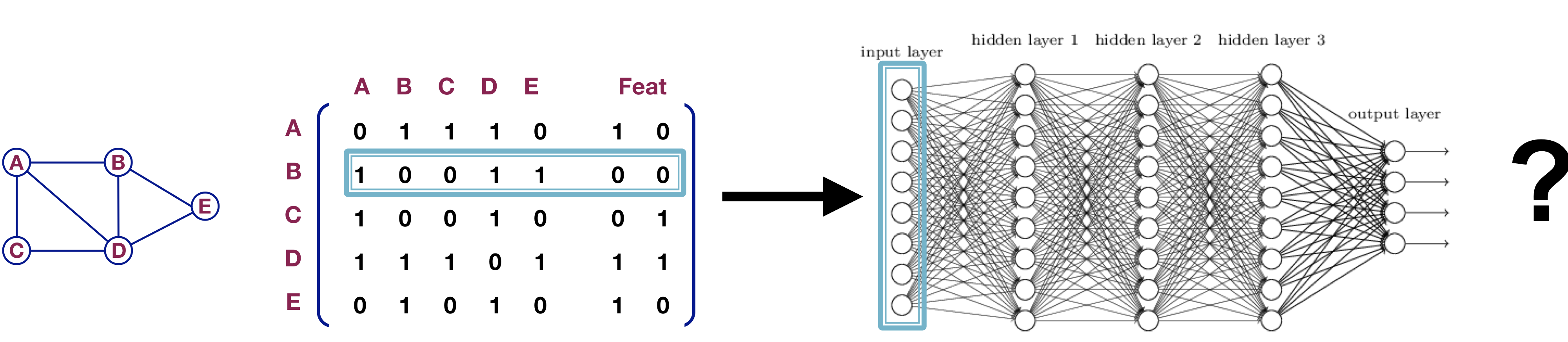
인접행렬과 특징(features)를 결합시킨 후 deep neural net의 입력으로 사용

문제점

• $O(|V|)$ parameters -> data 수가 많아지면 parameter 수도 많아짐
• 다른 크기의 그래프에 적용이 불가능
• 노드(node) 순서에 민감

---

Graph Convolutional Networks(GCN)

Convolution

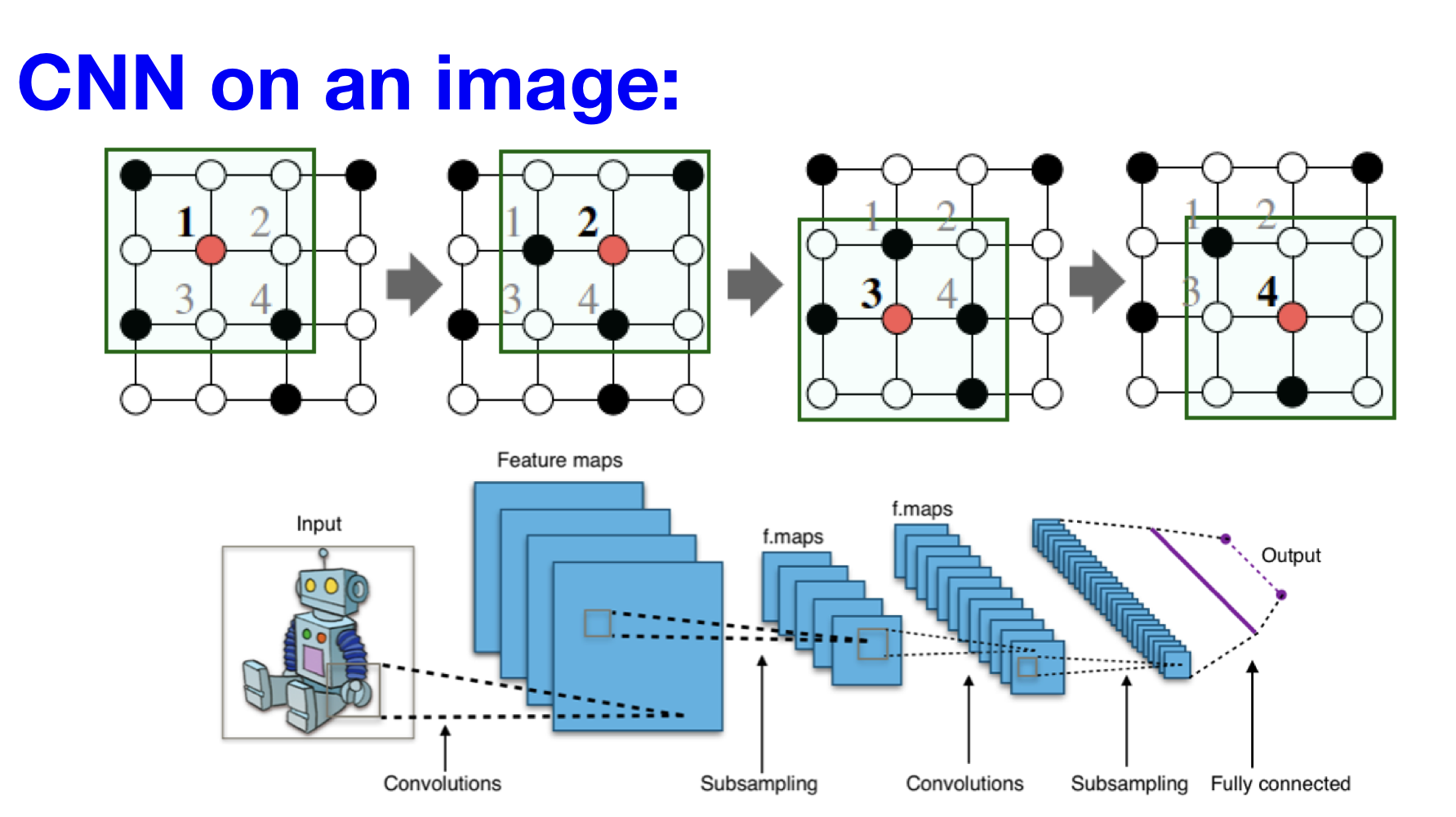
합성곱(convolution) 연산을 sliding window 방식에 따라 수행해 입력의 특징(feature)를 포착하는 신경망 구조

합성곱 연산의 idea: 주변 정보(neighbors)를 변환(transform)하고, 이를 결합(combine)

그래프의 구조적 특성 때문에 기존의 합성곱 연산을 적용하는데 어려움 존재

• No fixed notion of locality or sliding window on the graph
• Graph is permutation invariant

permutation invariant

• $f(x_1, x_2, x_3)$ = $f(x_1, x_3, x_2)$, $f$: model
• 즉, 모델 출력에 입력 벡터의 순서가 영향을 미치지 않는 데이터를 permutation invariant 하다고 한다.

---

Aggregate Neighbors

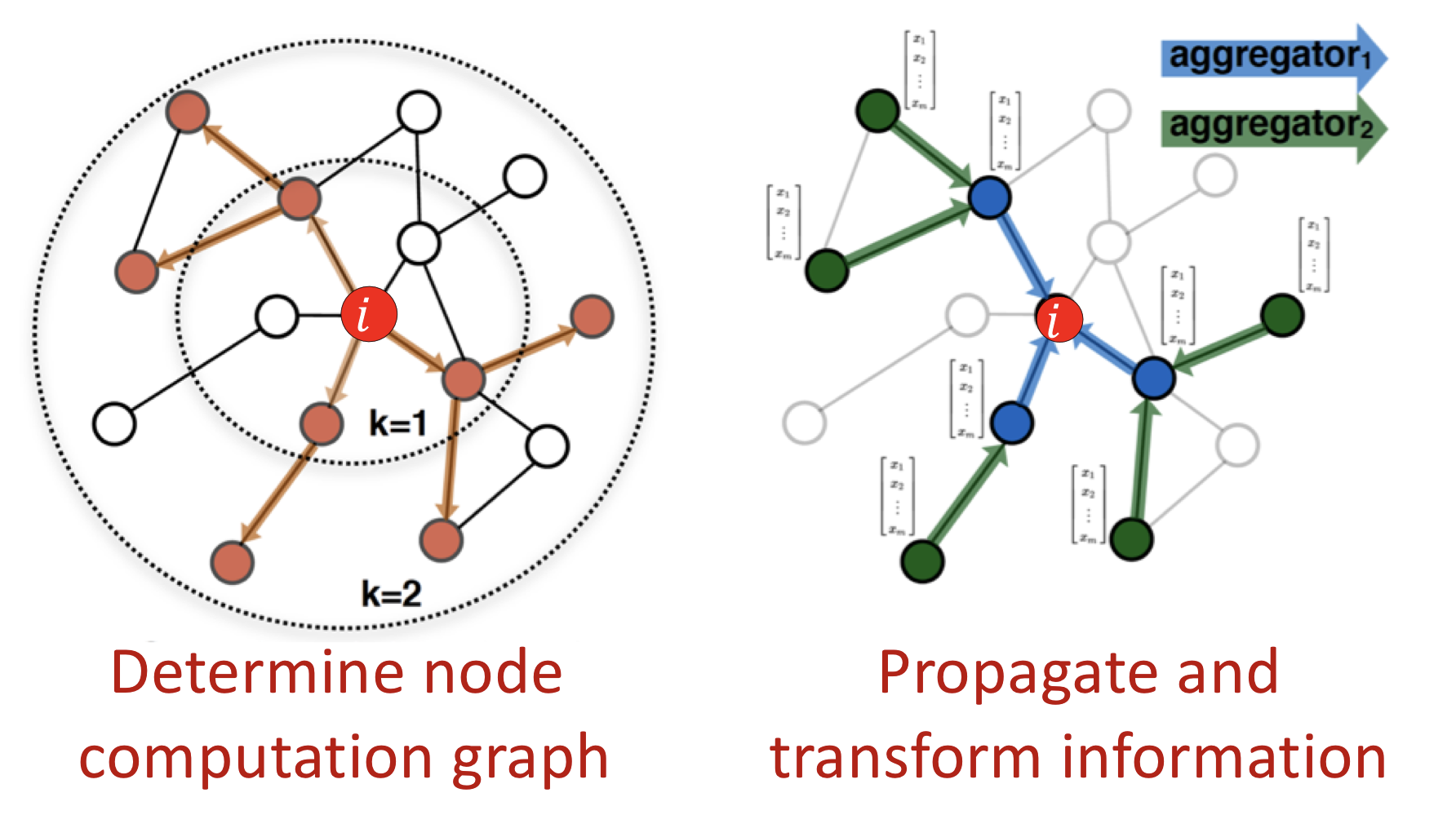
합성곱 연산의 idea를 다음과 같은 방식으로 그래프에 적용한다.

• Computation graph를 정의
• 정보 전파(propagate) 및 변환(transform)

Key idea: Generate node embeddings based on local network neighborhoods

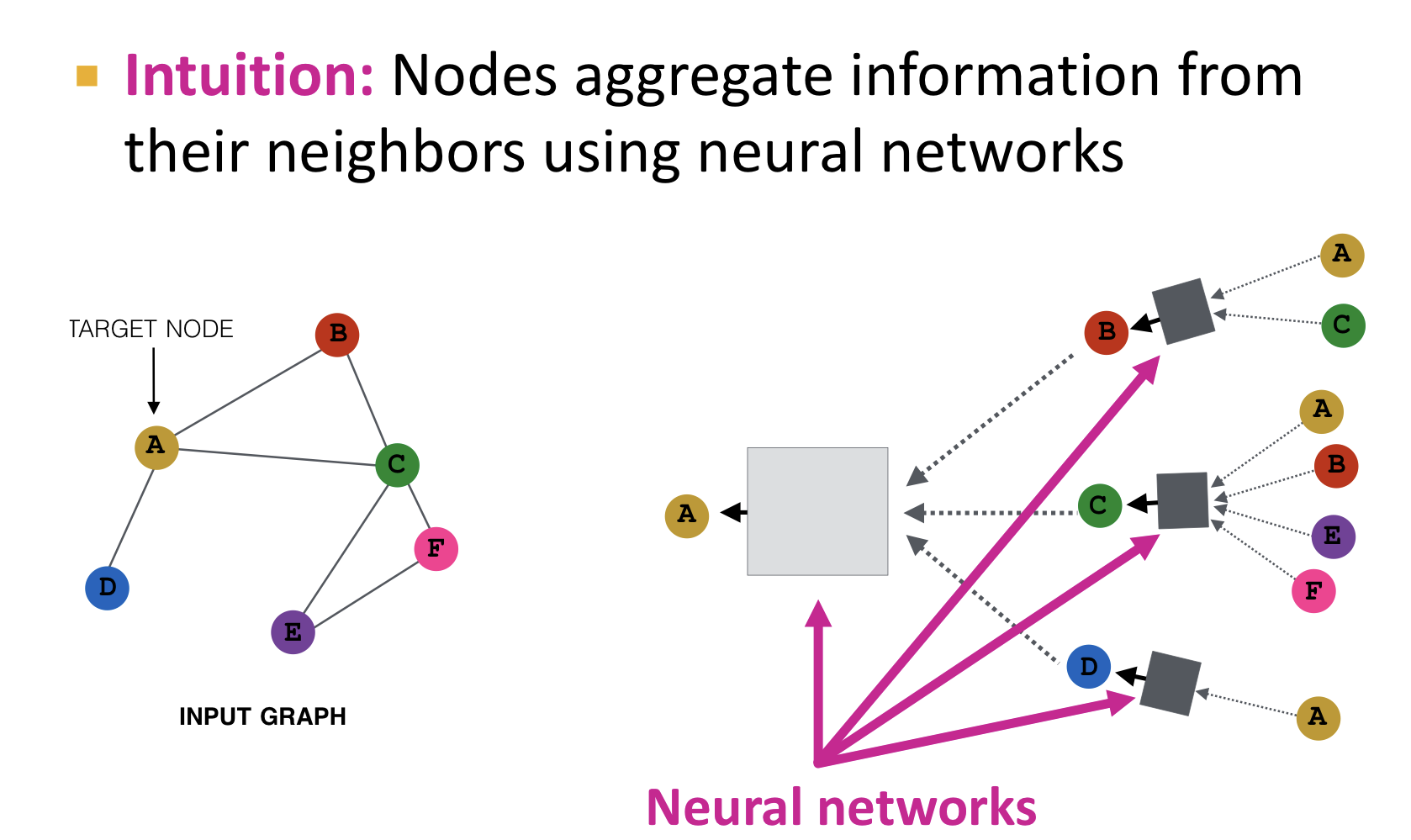
• 노드들은 신경망을 이용한 이웃 노드들의 정보를 합산(aggregate)한다.
• 모든 노드들은 노드마다의 인접 노드들에 기반해서 computation graph를 정의한다.

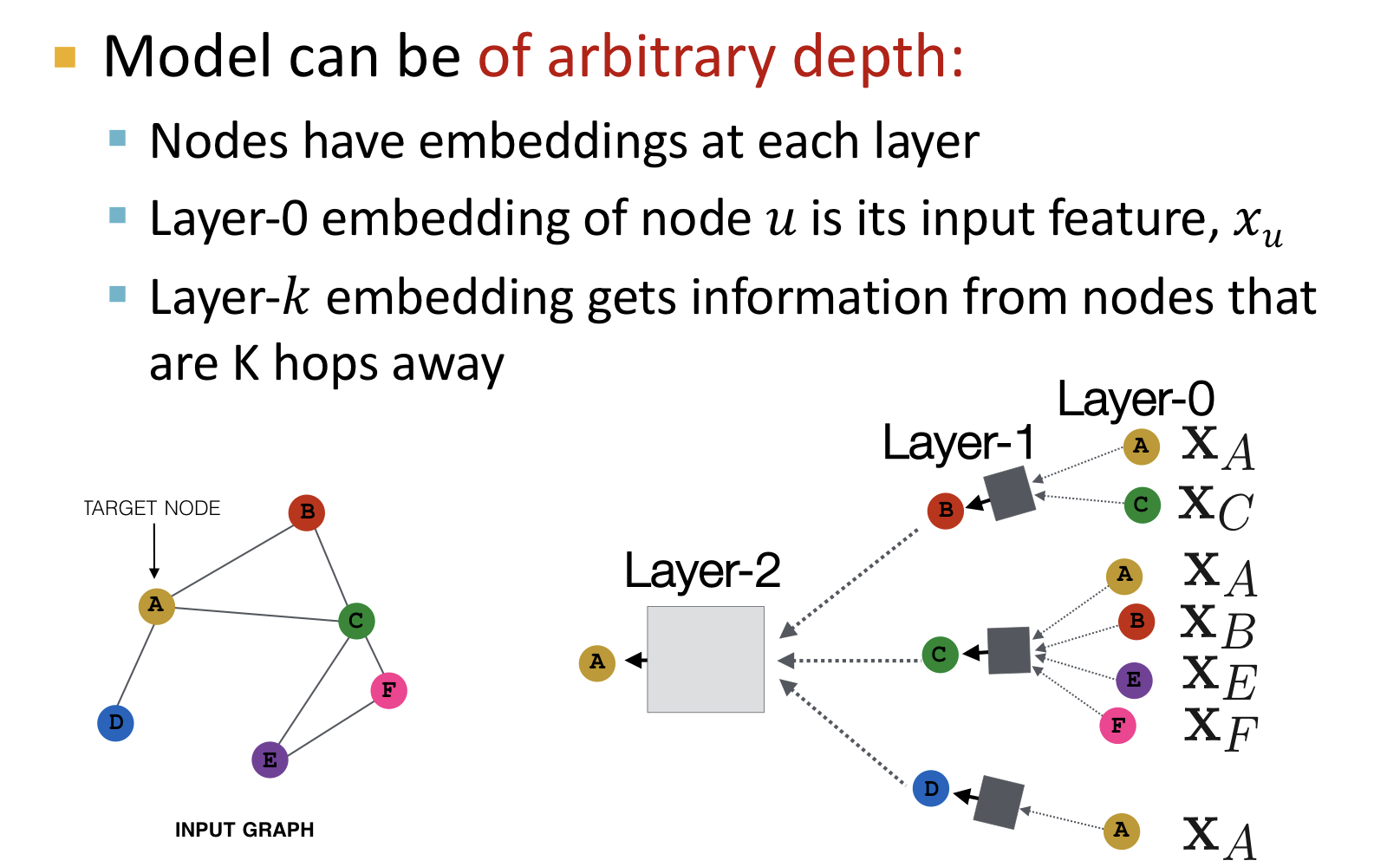
모델은 임의의 깊이를 갖을 수 있다.

• 노드들은 각각의 층(layer)에서 ebedding을 갖는다.
• Layer-0의 embedding은 해당 노드의 입력 특징(feature)이다.
• Layer-k의 embedding은 k만큼 떨어진 노드들로부터 정보를 갖고 온다.

---

Neighborhood Aggregation

인접 노드의 정보를 어떻게 합산(aggregate) 하는지에 따라 네트워크가 구분된다. 즉, aggregate operator에 따라 구분된다. 주의할 점은 graph의 특성인 permutation invariant를 고려해서 aggregate operator 또한 permutation invariant한 연산이어야 한다.

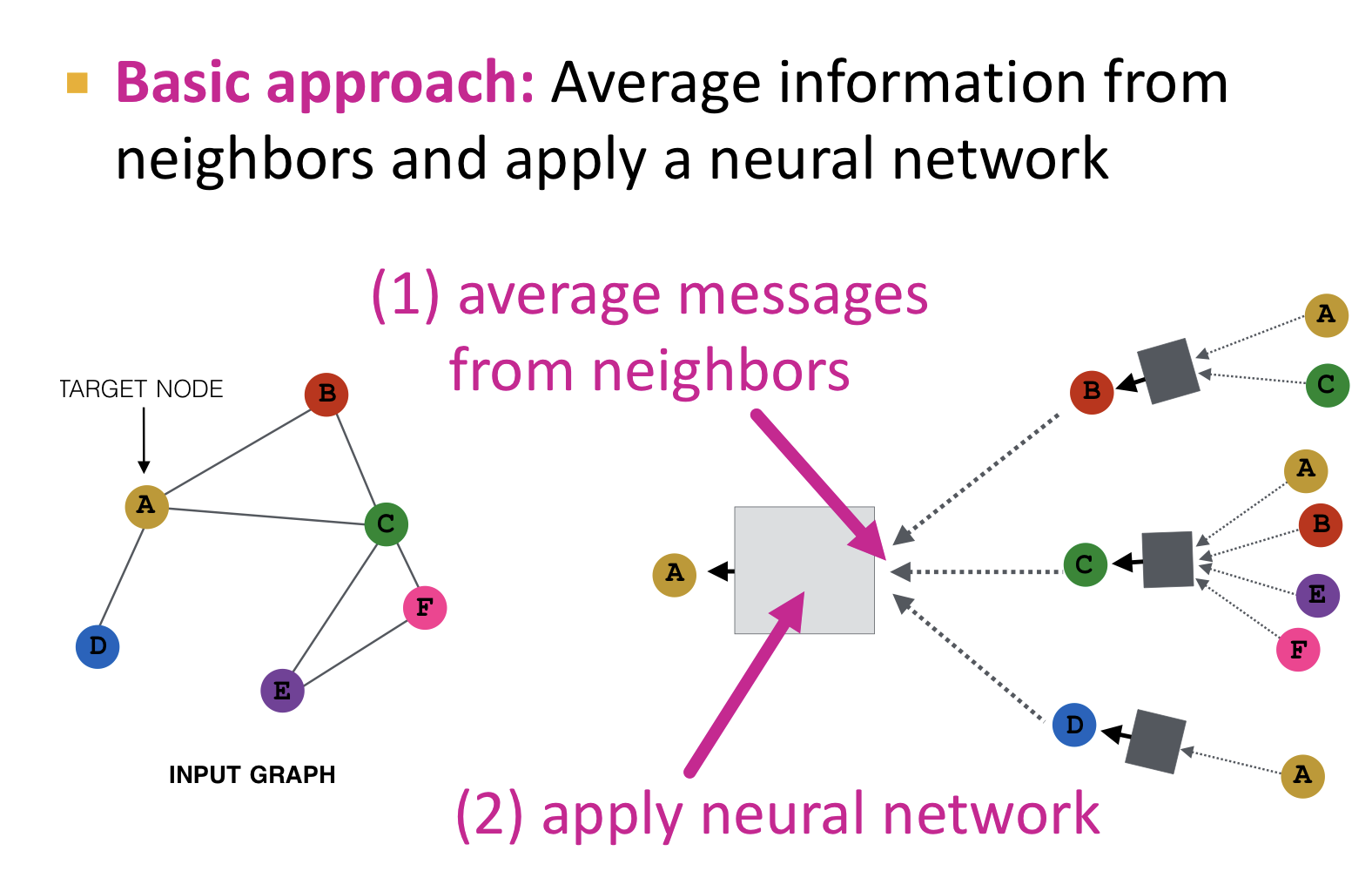
기본적인 방법으로 평균을 이용하는 방법이 있다.

1. 인접 노드들의 정보를 평균으로 합산
2. 신경망을 적용

수식으로는 다음과 같이 표현된다.

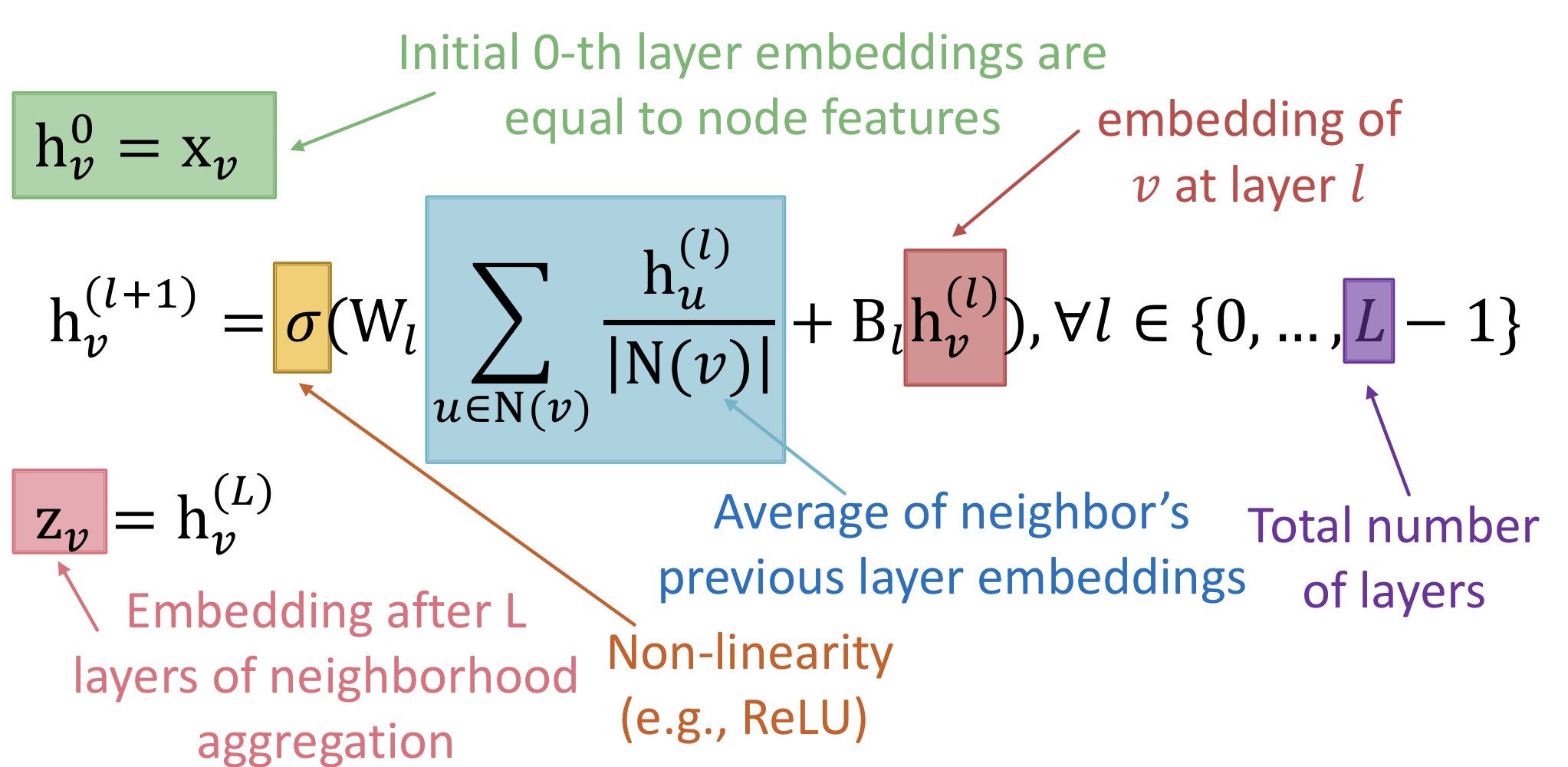
• $h_v^l$: $l$층(layer $l$)에서 node $v$의 embedding(hidden representation)

• $W_k$: 이웃 노드 합산(aggregate)을 위한 가중치 행렬 -> trainable

• $B_k$: 자기 자신의 변환(transform)을 위한 가중치 행렬 -> trainable

최종 layer에서의 node embedding을 loss function에 넣고 SGD를 이용해 학습을 진행한다.

---

Matrix Formulation

이웃 노드 정보를 합산(aggregate)하는 과정을 위와 같은 행렬 형태로 나타낼 수 있다.

• $A$: 인접행렬로 연결된 이웃 노드들의 embedding을 합(summation)하는 역할
• $D^{-1}$: degree의 역수로 이루어진 대각 행렬로 이웃 노드 수로 나누는 역할

즉, 업데이트 과정을 위와 같이 행렬 형태로 표현할 수 있다.
$\tilde{A}$가 sparse 하므로 효율적인 sparse matrix multiplication을 사용할 수 있다.

대부분의 GNN의 aggregation 연산을 위와 같은 행렬 형태로 수행할 수 있다. 하지만 aggregation function이 복잡한 경우 불가능한 경우도 존재

---

Train a GNN

Unsupervised Training

inner product와 같은 similarity를 이용해 인접한 노드들은 비슷한 embedding을 갖게 하는 방법

Supervised Training

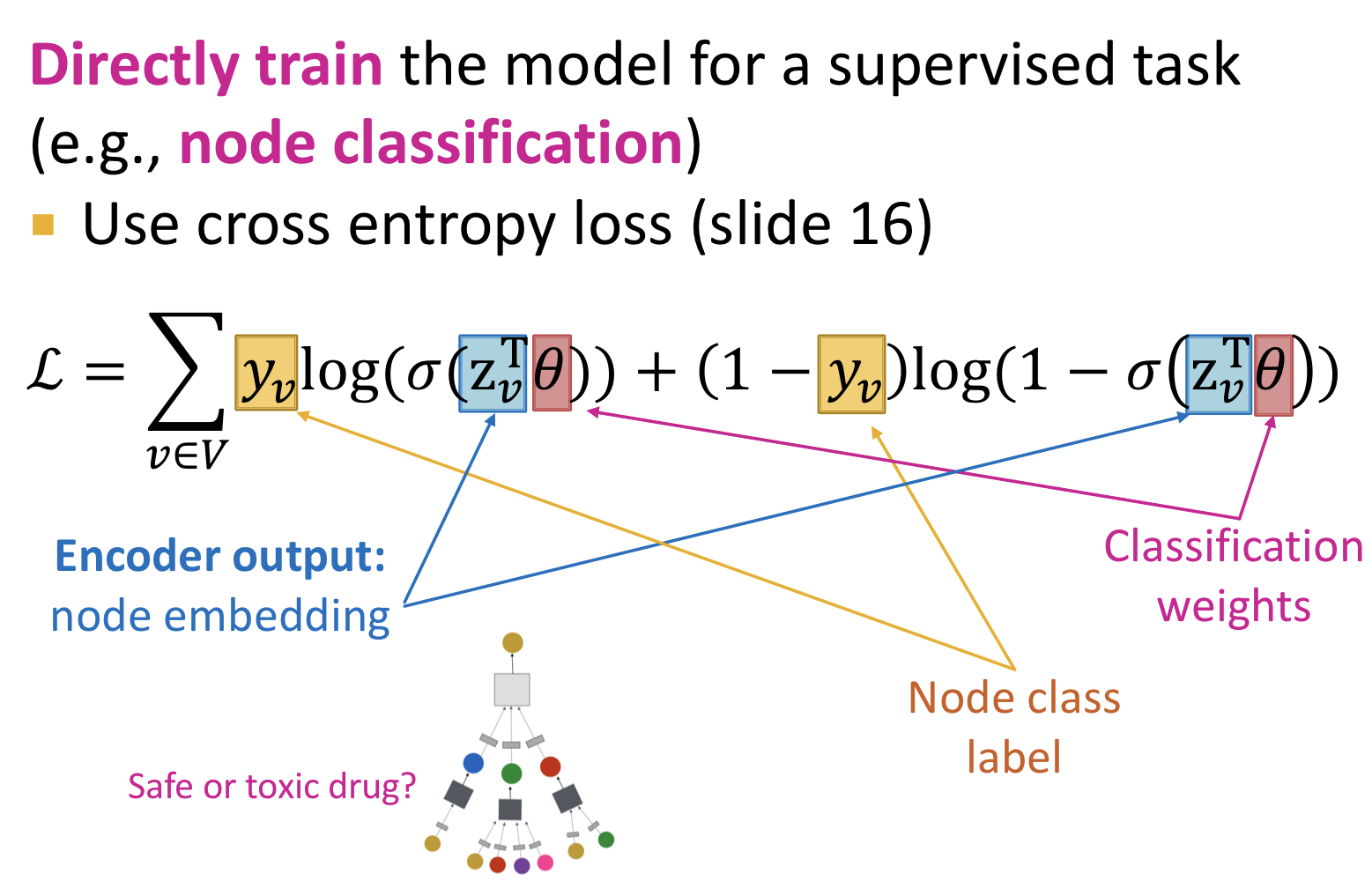
GNN을 통한 node embedding에 classification weights를 곱한 후 cross entropy loss를 적용하여 분류 문제를 해결할 수 있다.

---

Overview

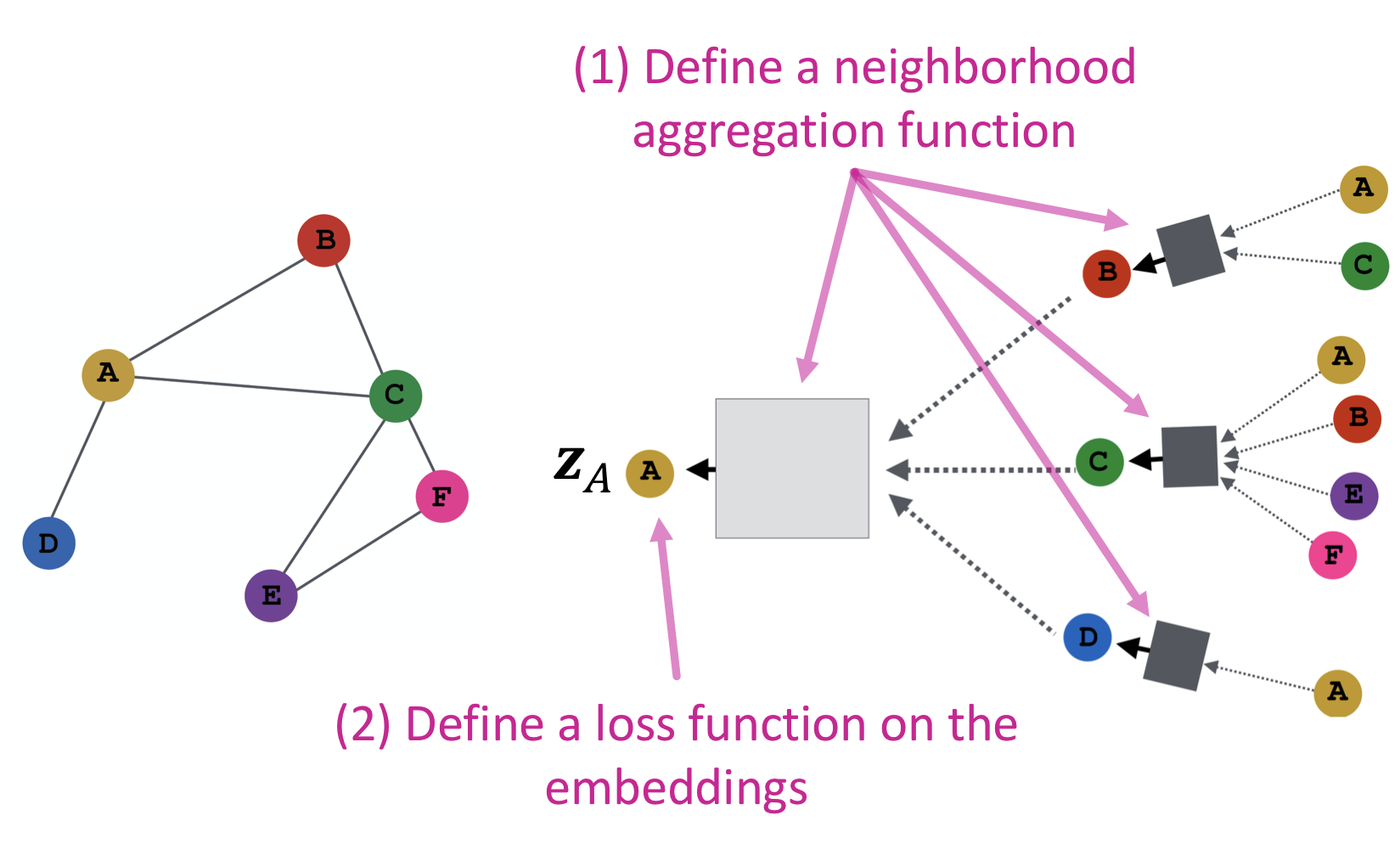
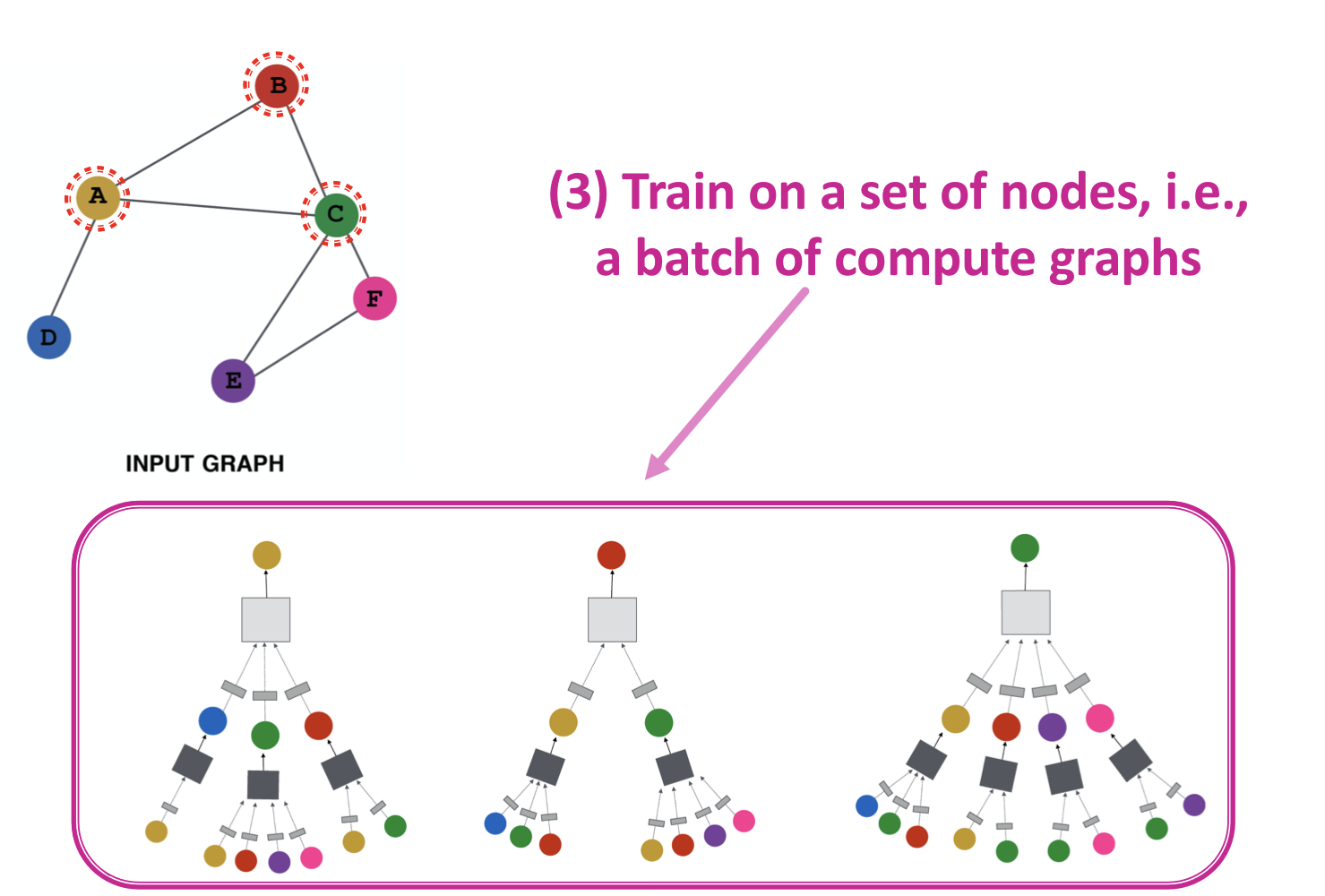
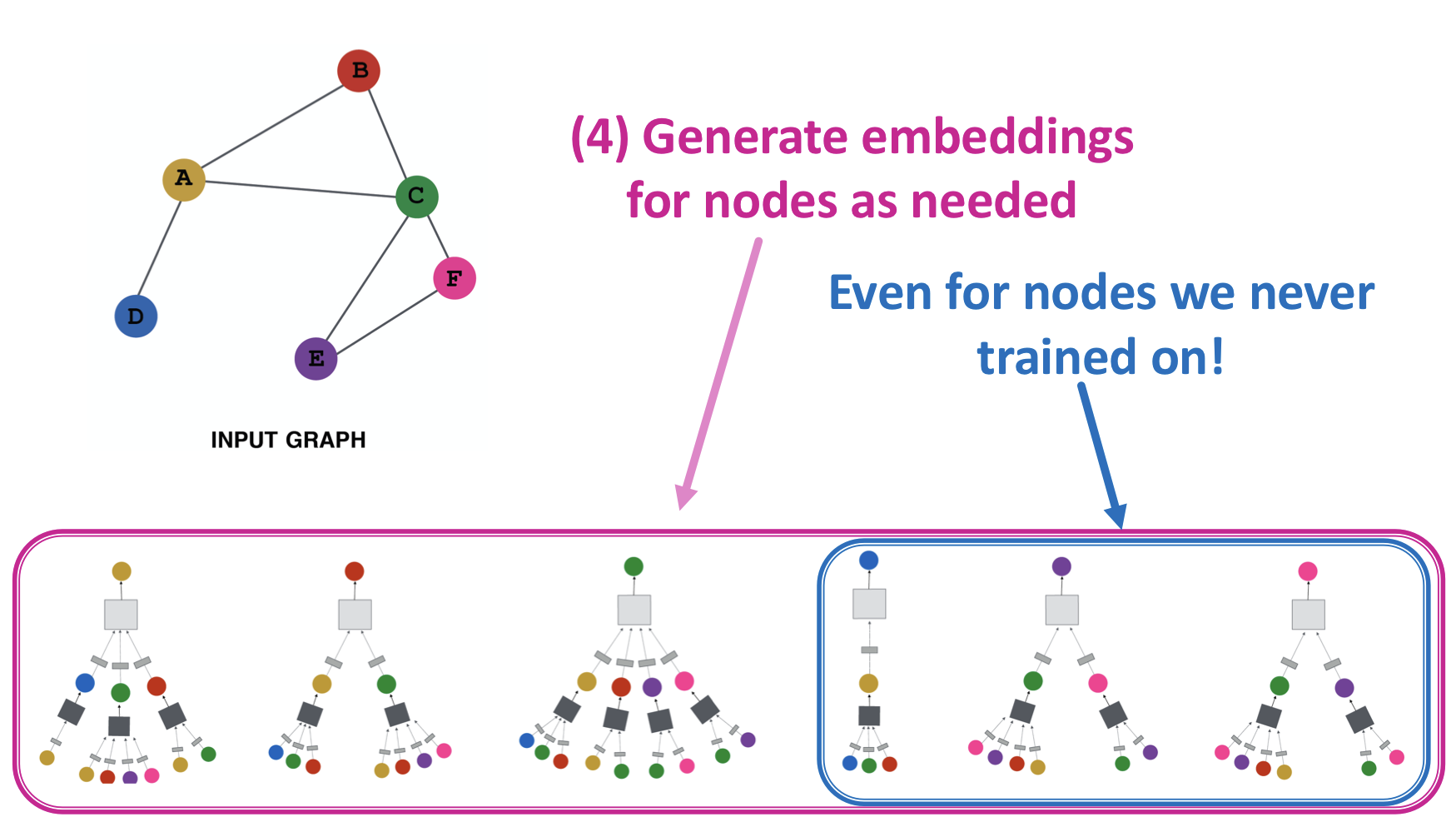
1. 인접 노드 합산(aggregate) 함수 정의
2. embedding에 적용할 loss function 정의
3. 노드 집합 학습
4. 필요한 노드의 embedding 생성

---

Inductive Capability

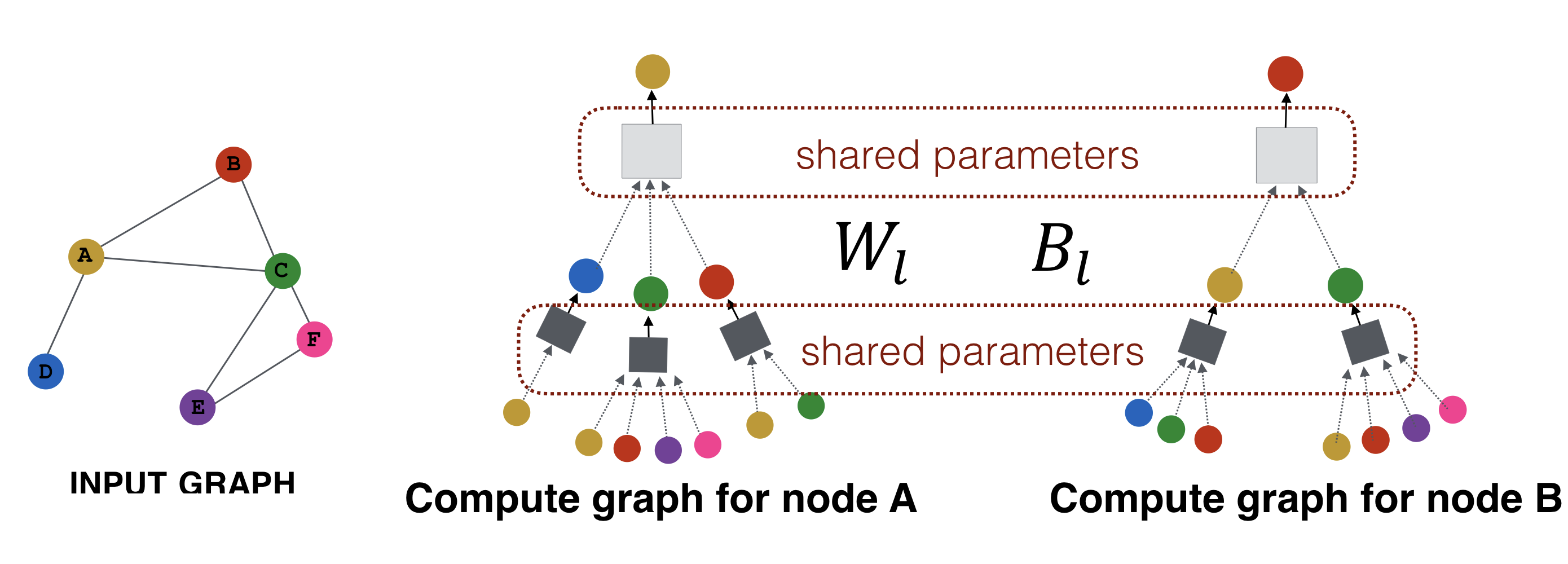
Aggregation parameters들이 모든 노드들에 대해 공유된다. 같은 층(layer)의 신경망은 학습 가중치를 공유한다.

• 모델의 parameter들이 노드의 개수에 준선형(sublinear)이다.
• 보지 못한 노드(unseen node)에 일반화가 가능하다.
  • 새로운 그래프에서 일반화 가능 ex) 유기체 A의 단백질 상호작용 그래프에서 학습한 모델을 통해 새롭게 취득된 데이터인 유기체 B의 embedding을 생성
  • 새로 연결된 노드 embedding 가능 ex) Reddit, YouTube, Google Scholar

---

References

• 투빅스 1213 GNN 스터디 8강
• Permutation Invariant
• GCN paper: SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS