[프로그래머스] Lv3. 합승 택시 요금 - JavaScript

문제분류 : 코팅테스트 연습

난이도 : Level 3

출처 : 프로그래머스 - 합승 택시 요금

문제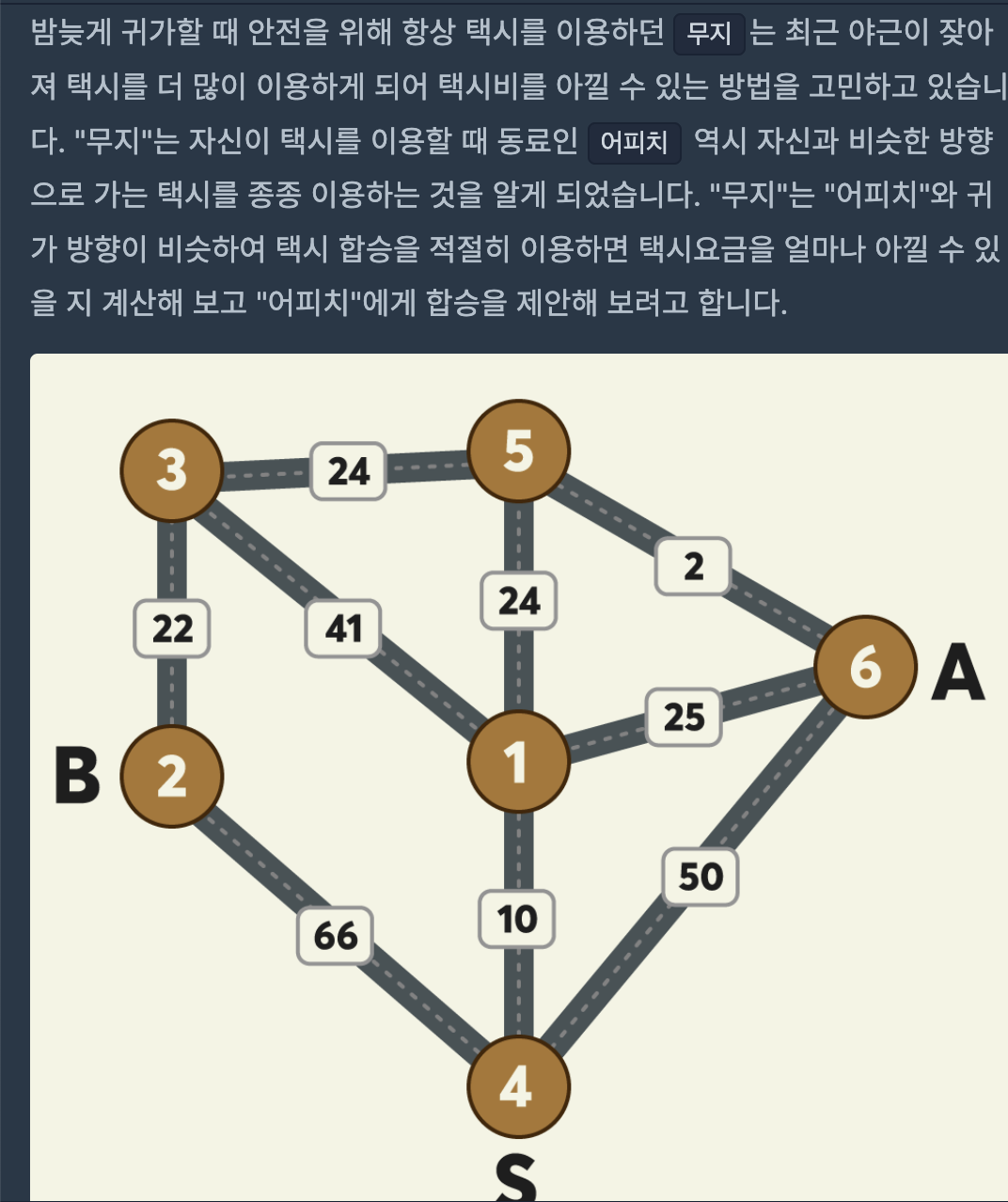

제한사항

📌 내가 생각한 풀이

플로이드 와샬 알고리즘을 이용하여, 모든 정점에서 모든 정점까지의 최단경로를 구하자. 그 이후 0~N까지 합승을 한다고 가정한 후, 합승을 하고 내린 지점부터 각자 도착지까지의 요금의 합이 가장 낮은 부분을 찾는다.

function solution(n, s, a, b, fares) {
    var answer = 0;
    let min = Infinity
    let graph = Array.from(Array(n), ()=>Array(n).fill(Infinity));
    fares.map((data,idx)=>{
        let [c,d,f] = data;
        graph[c-1][d-1] = f;
        graph[d-1][c-1] = f;
    })
    for(var i =0; i<n; i++){
        graph[i][i] = 0;
    }
    const floyd = () =>{
        for(var i =0; i<n; i++){
            for(var j =0; j<n; j++){
                for(var k =0; k<n; k++){
                    graph[j][k] = Math.min(graph[j][k], graph[j][i] + graph[i][k]) 
                }
            }
        }
    }
    floyd();
    for(var k = 0; k<n; k++){
        min = Math.min(min, graph[s-1][k]+graph[k][a-1]+graph[k][b-1])
    }
    return min
    
    
}

📌 느낀점

플로이드 와샬 알고리즘을 이용하여 모든 정점에서 모든 정점까지의 최단경로를 구할 수 있어야 풀리는 문제였다. 따로 플로이드와샬 알고리즘, 다익스트라 알고리즘을 정리해야겠다.