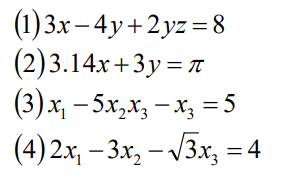2023.09.12

Linear Algebra

Mathematics?

복잡한 문제를 효율적으로 풀기 위해 주어진 문제를 숫자나 기호로 표기

Algebra?

어떤 식을 풀기 위해 숫자를 문자로 대체하는 수학.

Linear Algebra?

Vectors, Vector Space, matrices, linear transformation, linear equations 를 다룸.

Linear?

집합 A의 원소가 집합 A의 다른 원소들의 linear combination으로 표현될 수 있을 때.

Linear combination : 모르는 값들에 스칼라를 곱하고 그것들을 더함.
𝑎1𝐱1 + 𝑎2𝐱2 + ⋯ + 𝑎NxN
Unknown 값들에 대한 linear combination이다.

Equation vs Function

Equation : 좌항이 있고 우항이 있고, 그 둘이 같습니다.
Function : 함수는 규칙을 설명하고 있는 것이다.

Linear Function은 1차식만 포함. 지수가 있으면 안 된다. 1:1 결과가 나옴.
Linear function만 matrix로 표현할 수 있다.

Linear System

Linear Equation 을 여러 개 모아놓은 것. 근데 각 linear equation 에서 사용한 미지수가 같아야 한다. 즉, 한 시스템의 연립방정식에 대해 미지수를 찾으면 그 linear system 의 해를 찾았다. 라고 하는 것.

해가 존재하는 linear system - Consistent linear system 최소 하나의 해를 갖고 있음.
해가 존재하지 않은 linear system - Inconsistent linear system

General Linear system

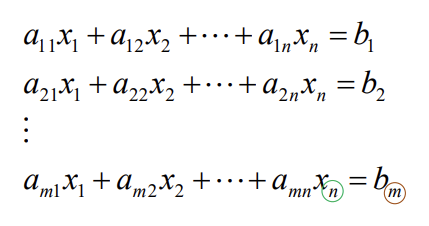
Homogenous Linear system

If b1 = b2 = … = b m = 0, it is called a homogeneous linear system

homogenous는 최소 하나의 해가 반드시 존재한다.
x1 = x 2 = … = x n = 0
이 해를, trivial soultion of the homongenous linear system 이라 한다.

이 중 하나라도 0이 아닌 해가 존재한다면, 이를 nontrivial solution이라 한다.

두 Linear system의 solution set가 같다면, 그 둘은 서로 equivalent하다 한다.

Visualization of Linear system

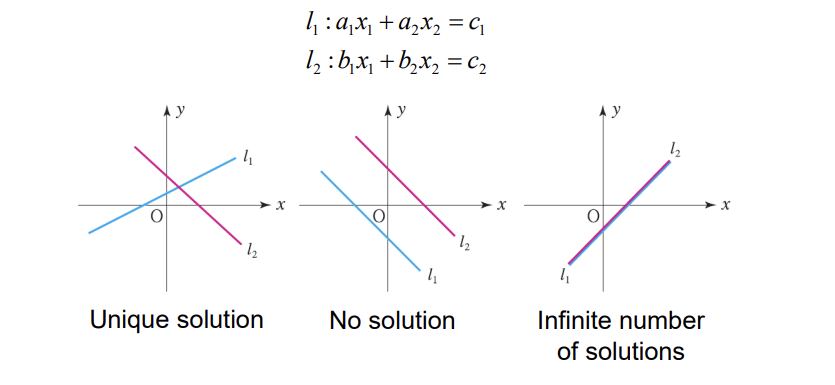
두 Linear Equation이 교차할 경우 : 한 가지 해 존재(Unique Solution)
두 Linear Equation이 평행하면서 떨어진 경우 : 해가 존재하지 않는다.
두 Linear Equation이 평행하면서 같은 경우 : 해가 무수히 많다.

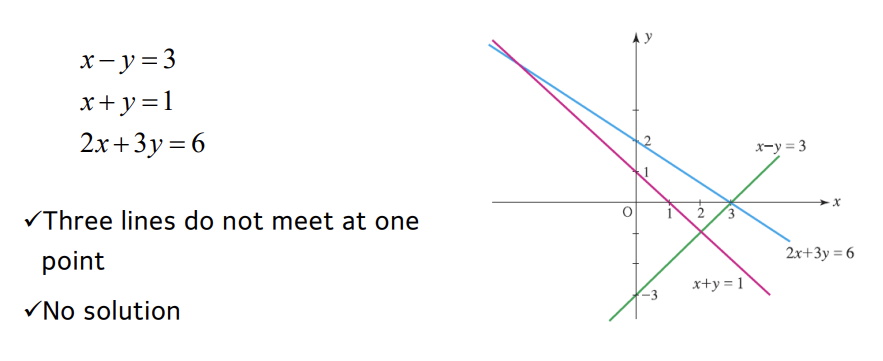
세 Linear Equation이 한 점에서 만나지 않는 경우 해가 존재하지 않는다.

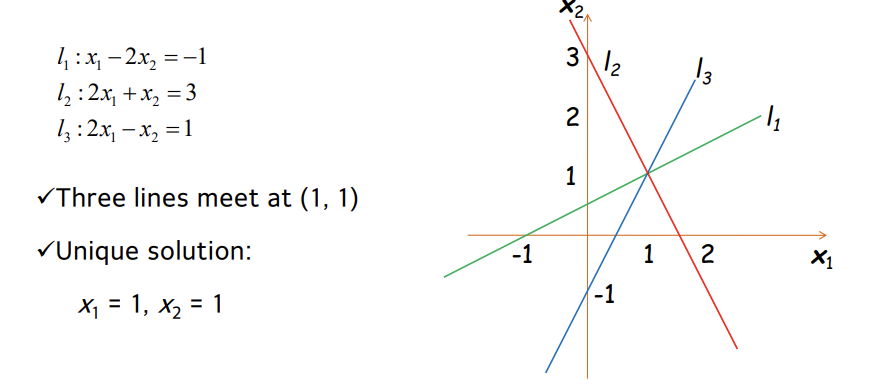
이럴 때 해가 하나 존재한다.

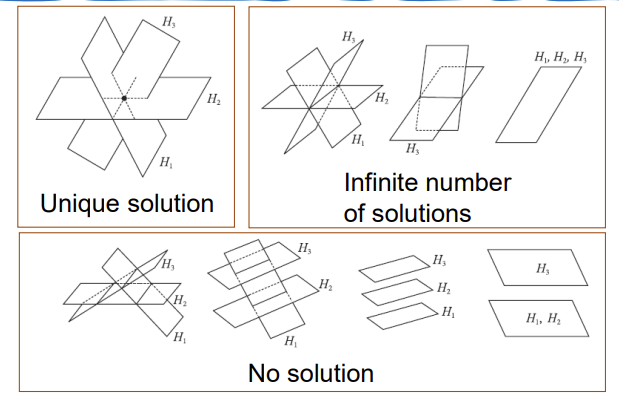
3차원의 경우, 하나의 선분에서 겹친다면 그 선분에는 무한한 점이 존재하기 때문에 해가 무수히 많다.

Solution Sets of Linear Systems

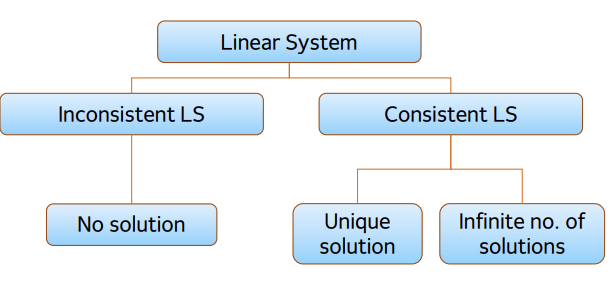
결국 해가 없거나, 하나만 있거나, 무수히 많은 경우만 존재한다.
해가 두 개 있거나, 세 개 있는 그런 것은 존재하지 않는다.

Exercise

• A linear system includes addition and multiplication only. ( T / F )
• The difference between a linear equation and a linear system is the number of equations to create them. ( T / F )
• Generally, second- and higher order-equations are linear equations. ( T / F )
• If a linear system has a solution, it is a unique solution. ( T / F )
• The set of following equations is a homogeneous linear system ( T / F )
  
• Choose a linear system that has a trivial solution only. ( 2 )
  
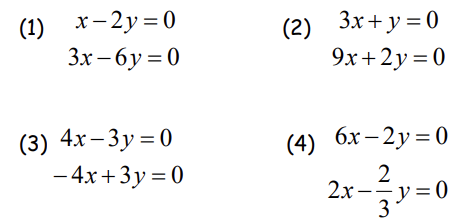
• Decide which equations are linear equations. ( 2, 4 )