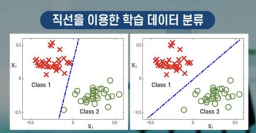
SVM의 최적화 목적 함수

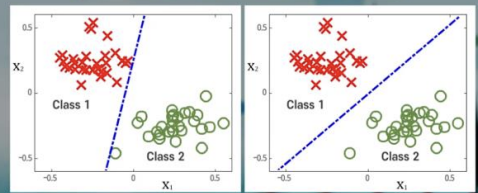
오른쪽의 그래프가 더 큰 마진을 가지고 분류하기 때문에 새로운 데이터를 더 잘 분류할 것.

• SVM(Support Vector Machine) : 곡선을 직선으로 근사화 한 것

• SVM은 직선의 형태이기 때문에, 계산량 면에서 많이 유리함

• 강의에선 로지스틱 회귀에 사용되는 sigmoid 함수의 비용함수를 SVM으로 만듦

• 위에서부터 차례대로, 로지스틱 회귀 비용함수, SVM 근사, 데이터 개수 곱하고, 람다의 역수를 곱한 식

• 비용함수에 상수를 곱하거나 나누어도, 최솟값을 만드는 파라미터는 동일하다

• SVM 사용을 통해, 더 적은 계산량으로 최적 파라미터를 구할 수 있음.

최대 마진 개념

• Safety Margin : 데이터를 분류하는 데 애매한 상태가 나타나지 않도록 설정하는 여백
• 비용함수에 정규화 항만 남게 됨
• 이 비용함수를 최소로 하는 파라미터를 찾음
• Outlier : 같은 값을 가지는 데이터들과 매우 다른 특성을 가지고 있는 항목. 주로 데이터 수집과정에서의 실수에 의해 발생.

최대 마진 분류의 수학적 개념

• SVM에서 가중치 벡터에 대한 데이터 투영이 클수록 비용함수의 값이 작아짐

• 마진을 최대화하는 방향으로 최적화, Separating Margin을 최대화해서 SVM Decision Boundary를 만들면, 일반화 성능 우수, 새로운 데이터도 성공적으로 분류할 수 있음

커널의 개념

• 위에선 분류경계선이 직선이었지만, 더 복잡한 데이터의 분류를 위해선 더 복잡한 분류경계
  선이 필요함 -> 커널 사용으로 해결 가능

• 커널: 주어진 데이터와 랜드마크 사이의 유사도

• 여기서 랜드마크는 처음엔 수동으로 설정, 각 데이터들이 랜드마크에서 얼마나 떨어져 있는지를 고려해서 Decision Boundary 생성

• 여기서 C의 값이 너무 크거나 작을 경우 overfitting 혹은 underfitting 문제가 발생함

• 가우시안 커널을 사용했을 때, 데이터 x가 랜드마크에 가까우면 특징값은 1에 가깝고, 멀면 0에 가깝다.

비지도 학습의 목적과 사례

• Clustering : 데이터들의 특성이 유사한 데이터끼리 묶는 것
• Clustering 은 곧 비지도 학습의 목적
• Clustering의 예) 소비자 그룹을 소비 패턴에 따라 나누기
• Clustering을 잘하면 이상데이터 검출에도 활용할 수 잇음

K-means 알고리즘의 원리

• K-Means 알고리즘 : Clustering 알고리즘 중에서 사용도가 높은 알고리즘
• 2단계를 반복하는데, 1- Cluster Assignment, 2- Centroid Movement.
• 처음에는 그냥 랜덤하게 Cluster Assignment
• 각 데이터들마다 가장 가까운 클러스터를 지정
• 각 Centroid는 자기를 지정한 데이터들의 중점으로 본인을 이동 -> Centroid Movement

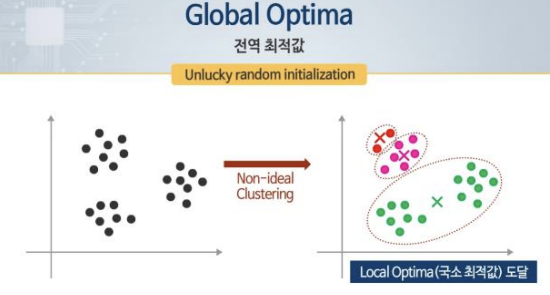
랜덤 초기화와 K-Means 알고리즘

• 초기에 랜덤으로 centroids 설정하는 과정이 K-Means 알고리즘 수렴에 영향을 줄 수 있
  음
• 국소적으론 최적의 clustering을 이뤄냈지만, 전역적으론 그렇지 않은 문제 발생 가능함
• 이를 Local Optimum이라하고, 이를 피하기 위해서 Cluster를 여러 번 반복해서 초기화하면 됨
• 예를 들어, 랜덤하게 초기 centroid를 초기화하고 K-Means 알고리즘을 100번 수행한 후, 비용함수 값을 비교해서, 비용함수를 최소로 만드는초기 centroid 세팅을 사용하면 됨
• 다만 클러스터의 개수가 많으면 랜덤초기화를 여러 번 수행하더라도 도움을 기대할 수 없음
  

클러스터 수의 결정

• K(클러스터 수) 값의 명확한 답은 존재하지 않음
• 다만 Elbow Method를 통해 유추 가능
• Elbow Method : 도식화했을 때 '급격하게 변하는 부분이 최적의 세팅이다' 라고 생각하는 방법.
• 다만 항상 이상적인 결과를 제시하진 않음
  따라서 K값의 설정은 직접 설정, elbow method, 목적에 기반한 설정 등으로 할 수 있다.
  

차원 줄이기

• 높은 차원의 데이터는 계산에 많은 시간이 소요.
• 차원줄이기 : 높은 차원의 데이터 특성은 유지하되, 낮은 차원의 벡터로 표현
• 2개의 매우 높은 상관간계를 보이는 특징 값을 하나의 특징 값으로 변환 (2차원->1차원)
• 데이터 압축의 목적 : 저장공간 확보, 학습 속도 향상

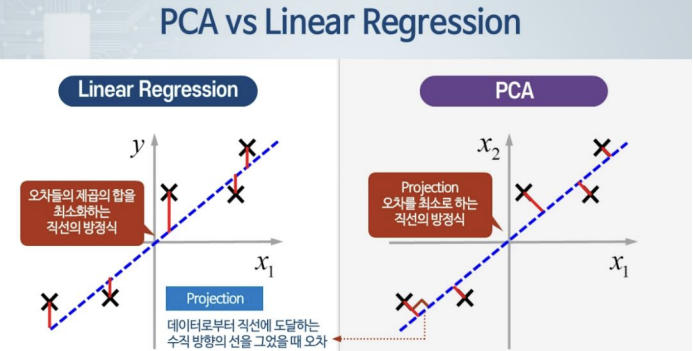
PCA(Principal Component Analysis)

• PCA : 차원을 줄이기 위해, 낮은 차원의 평면을 찾아내어 데이터를 projection시키는 것
• 가장 적절한 방향의 평면을 찾아내는 것이 관건
• 직선에 투영시킨 거리가 작을수록 좋은 Projection, 좋은 평면
  

PCA 알고리즘

• PCA 알고리즘을 수행하기 전에 데이터 전처리를 해주어야 함.
• 데이터 전처리엔 2가지 종류가 있음(평균 정규화, 특징값 스케일링)
• 평균 정규화(Mean Normalization) : 각 값들을 평균값을 뺀 값으로 대체.
• Covariance matrix(sigma)

Principal Component 수 K의 결정

• K를 정하기 위해선 오차를 최소화시키는 것을 고르면 됨

PCA 적용 방법

• 데이터 압축, 데이터 시각화에 사용할 수 있음
• 데이터 시각화를 위해선 k값에 제한이 걸려있음
• 과적합 예방을 위해 PCA를 사용하는 것은 잘못
• 머신러닝을 처음부터 PCA를 사용해서 진행하는 것은 잘못됨

이상 데이터 검출 문제 정의

• 이상 데이터 : 많은 데이터 중에서 일반적으로 발생하지 않는 데이터(정상 범위에서 벗어난 특이한 데이터)
• 확률 분포모델을 만들고 출력 값이 임계값(threshold) 이상이면 괜찮은데, 미만이면 이상데이터

가우시안 분포(정규분포)

• 평균, 분산에 의해 정의됨
• 가우시안 그래프의 넓이는 항상 1
• 범위가 무한대로 모든 확률값 존재

다변수 가우시안 분포
: 서로 다른 특징값 간의 상관 관계를 자동으로 획득
: 공분산 행렬과 그 역행렬을 계산해야 할 필요가 있음

이상 데이터 검출 알고리즘

각 특징 값들이 독립시행 -> 확률분포를 계산할 때 각 확률분포 함수를 모두 곱해줘서 구할 수 있음

• 학습 데이터엔 이상 데이터를 포함하지 않은 정상 데이터만 하는 것이 좋고, Cross
  Validation, Test set에 이상데이터를 포함시켜서 모델을 구현하는 것이 좋다

• 다변수 가우시안 확률분포는 파라미터(평균값, covariance)) 에 따라 다른 모양으로 나옴

Quiz

1. 머신러닝 진단 테스트에 관한 다음 설명 중 올바른 것을 모두 고르시오.

a. 머신러닝 진단 테스트는 학습 알고리즘 성능을 향상시키기 위해서 어떤 방법들이 효과적인지 알려준다.
b. 예측함수를 평가하기 위해 우리는 데이터를 두 부분으로 나누는데, 약 50%는 학습용이고 50%는 테스트용이다. -> 70%가 학습용, 30%가 테스트용
c. 로지스틱 회귀에서는 오분류 비율을 테스트 set 오차의 대안으로 사용할 수 있다.

2. 모델 선택에 관한 다음 설명 중에서 올바른 것을 모두 고르시오

a. 모델 선택이란 새로운 데이터에 대해 일반화할 수 있는 가장 좋은 모델을 선택하는 문제이다.
b. 모델 선택이란 학습 오차가 가장 적은 최적의 모델을 선택하는 문제이다.
c. 검증 데이터 셋을 사용하여 모델을 선택하고, 테스트 셋을 이용하여 모델의 성능을 평가한다.

3. 다음 설명 중 머신러닝 시스템을 설계할 때 가장 먼저 고려하여야 할 사항은?

정답 : 접근방식 선택하기(지도학습 / 비지도학습)

4. 머신러닝 시스템 설계에서는 먼저 학습 알고리즘을 간단하고 손쉽게 구현해 보는것이 좋다. 그리고 하나의 숫자로 표현되는 ( ) 을 이용하여 ( )을 해 봄으로써 앞으로 어떻게 성능을 향상시켜야 하는지에 대한 아이디어를 얻을 수 있다.

정답 : 평가 척도, 오차 분석

5. SVM에 관한 다음 설명 중에서 올바른 것을 모두 고르시오.

정답 : 두 벡터 사이의 각도가 90도~270도 범위에 있으면 내적은 음수가 된다, SVM에서 가중치 벡터에 대한 데이터 투영이 클수록 비용 함수 값은 더 작아진다.

6. 가우시난 커널을 사용했을 때, 데이터 x가 랜드마크에 가까우면 특징값은 ( ) 에 가깝고, 데이터 x가 랜드마크에 멀리 떨어지면 특징값은 ( ) 에 가깝게 된다.

정답 : 1, 0

7. ( ) 학습은 라벨이 지정되지 않은 데이터를 학습하는 알고리즘이며, 그 중 하나의 예는 데이터의 구조적 특성을 찾는 ( ) 이다.

정답 : 비지도학습, 클러스터링

8. K-means 알고리즘에 관한 다음 설명 중에서 올바른 것을 모두 고르시오

정답: K-means 에서 최적화 목적함수는 각 클러스터 중심에서 데이터까지의 거리를 최소화하는 것이다., 최적화는 클러스터 할당 단계 및 클러스터 중심 업데이트 단계 모두에서 수행된다.

9. PCA에 관한 다음 설명 중 올바른 것을 모두 고르시오

a. PCA는 데이터를 투영하고자 하는 저차원 평면을 찾는다.
b. PCA에서는 평균 정규화가 필요하지만 특징값 스케일링은 필요하지 않다. -> 모두 필요하다
c. 좋은 PCA 투영은 데이터와 그것의 투영 사이의 거리를 최소화하는 것이다.