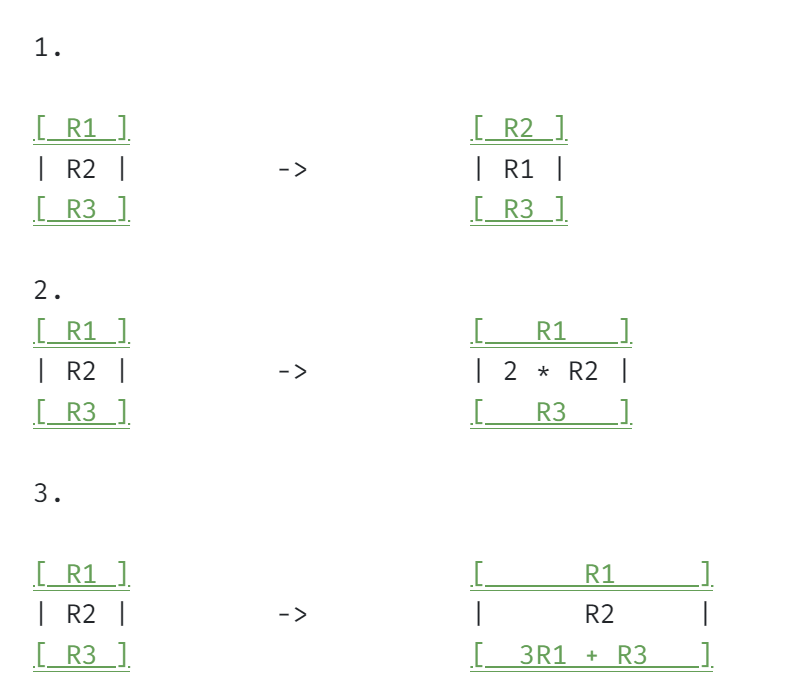
Elementary Row Operation
- Following three types of operations performed on a matrix are called elementary row operations
- Interchanging two rows ( 두 행을 서로 바꾸기)
- Multiplying a row by a nonzero constant (한 행에 0이 아닌 상수 값을 곱하기)
- Adding a multiple of a row to another row (한 행에 0이 아닌 상수 값을 곱한 후, 다른 행에 더하기)
Row Equivalent
만약 위의 ERO 연산을 통해 행렬 A를 행렬 B로 만들 수 있다면 두 행렬은 Row Equivalent 하다고 한다.
기호로는 A ~ B 라고 쓴다.
cf) A = B 와 A ~ B 를 구분하자. 앞은 Equal, 뒤는 Equivalent이다.
Equal은 모든 행렬의 요소 aij = bij 일 때를 의미한다.
Elementary Matrix
An n x n matrix E is called elementary if it is the result of performing a single elementary row operation on the identity matrix I.
✓If a square matrix A is multiplied with an elementary matrix E, the elementary row operation used to create the elementary matrix E is applied to the matrix A
만약 Elementary Matrix E가 ERO 1번 연산이 적용되었다고 해보자. A를 ERO 1번 연산을 통해 B를 만들 수 있다면, EA = B가 되며, A ~ B 라고 할 수 있다.
우리야 눈으로 당장 위 아래 바꾸면 되겠네 하는데, 컴퓨터는 연산을 해야하기 때문에 이런 식으로 연산을 해주어야 한다.
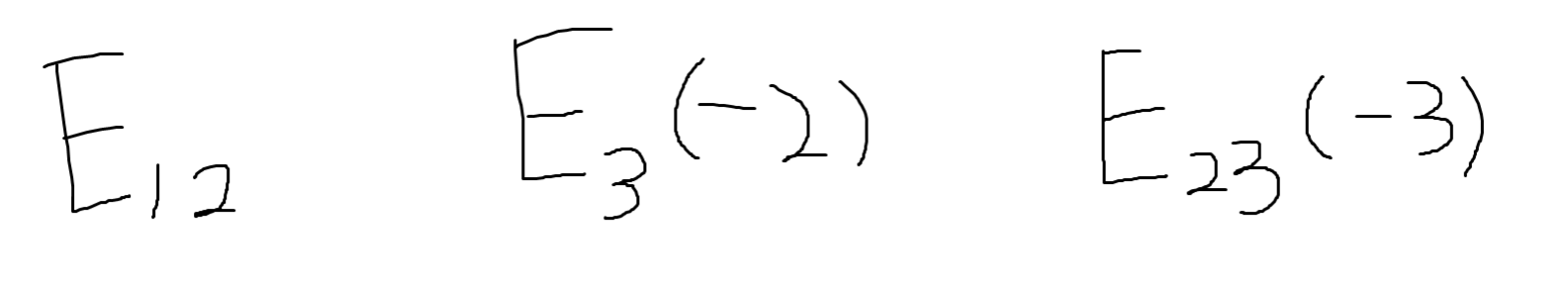
이런 기호를 사용해서 나타낸다.
첫 번째는 row 1과 row 2를 바꿈을 의미하며
두 번째는 row 3에 -2를 곱함을 의미하고
세 번째는 row 2에 -3을 곱한 후 row 3에 더한 것을 의미한다.
Pivot
The first nonzero entry in each row of a matrix can be chosen as a pivot
만약 1행 3열이 pivot이라면, 1행 1~2열까지는 다 0이라고 할 수 있다.
Row Echelon From (REF)
A m x n matrix A is in row echelon form if it satisfied following two conditions
1) The zero rows lie below any nonzero rows
zero row 가 있으면 반드시 nonzero row 밑에 있어야 한다.
zero row?
한 row의 모든 element 가 0인 row. 예를 들어 3X3 matrix에서 2행 1, 2, 3열의 요소가 0일 때 row 2는 zero row
123
000
400
은 1번 조건을 만족하지 않음.
123
400
000
은 1번 조건을 만족함.
2)The first nonzero entry (pivot) in a nonzero row lies to the right of the first nonzero entry (pivot) in the row immediately above it
pivot이 바로 위의 pivot보다 오른쪽에 있어야한다.
123
400
000
두 번째 row에 있는 피봇의 위치(4)가 첫 번째 row에 있는 피봇의 위치보다 오른쪽이지 않음.
2번 조건을 만족하지 않음.
123
040
000
은 2번 조건을 만족함.
이 두 조건을 모두 만족해야 REF 에 들어갈 수 있음.
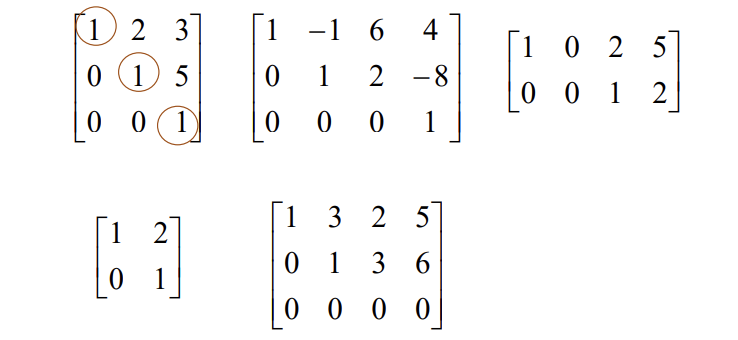
Reduced Row Echelon From (RREF)
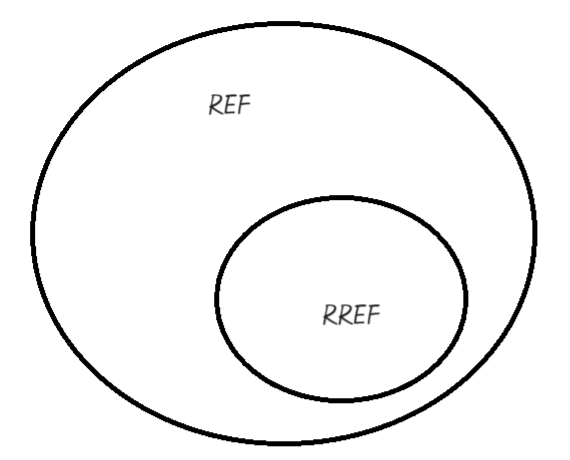
RREF 는 REF 에 속해있음.
따라서, REF가 아니라면 RREF가 될 수 없음
조건 ) 모든 pivot column에서, 모든 pivot has the value 1 and all other entries in the column are zero
예를 들어
123
004
000
일 때,
pivot이 존재하는 열인 1, 3열은 pivot column임.
두 번째 행의 피봇인 4는 1이 아니기 때문에, RREF가 될 수 없음.
123
001
000
일 때,
두 pivot 모두 1이지만, pivot column인 3열에 0이 아닌 값(3)이 존재하기 때문에 RREF가 아님.
Transform to RREF
A를 B(RREF)로 바꾸고 싶을 때
A -> B1(REF) -> B(RREF) 로 바꾸자.
Apply elementary row operations to set the entries below the pivot zero in a forward phase.
1) pivot 밑에 값들을 모두 0으로 만들어주기
Apply elementary row operations to set the entries above the
pivot zero in a backward phase
2) 다시 올라가면서 pivot 위의 값들을 모두 0으로 만들어주기
Rank
The rank of A is the number of nonzero rows in a row echelon form transformed from the matrix A
Rank(A) = rank(A ref)
row의 지배만 받을 것 같지만, rank의 최댓값은 row와 column의 최솟값이다.
