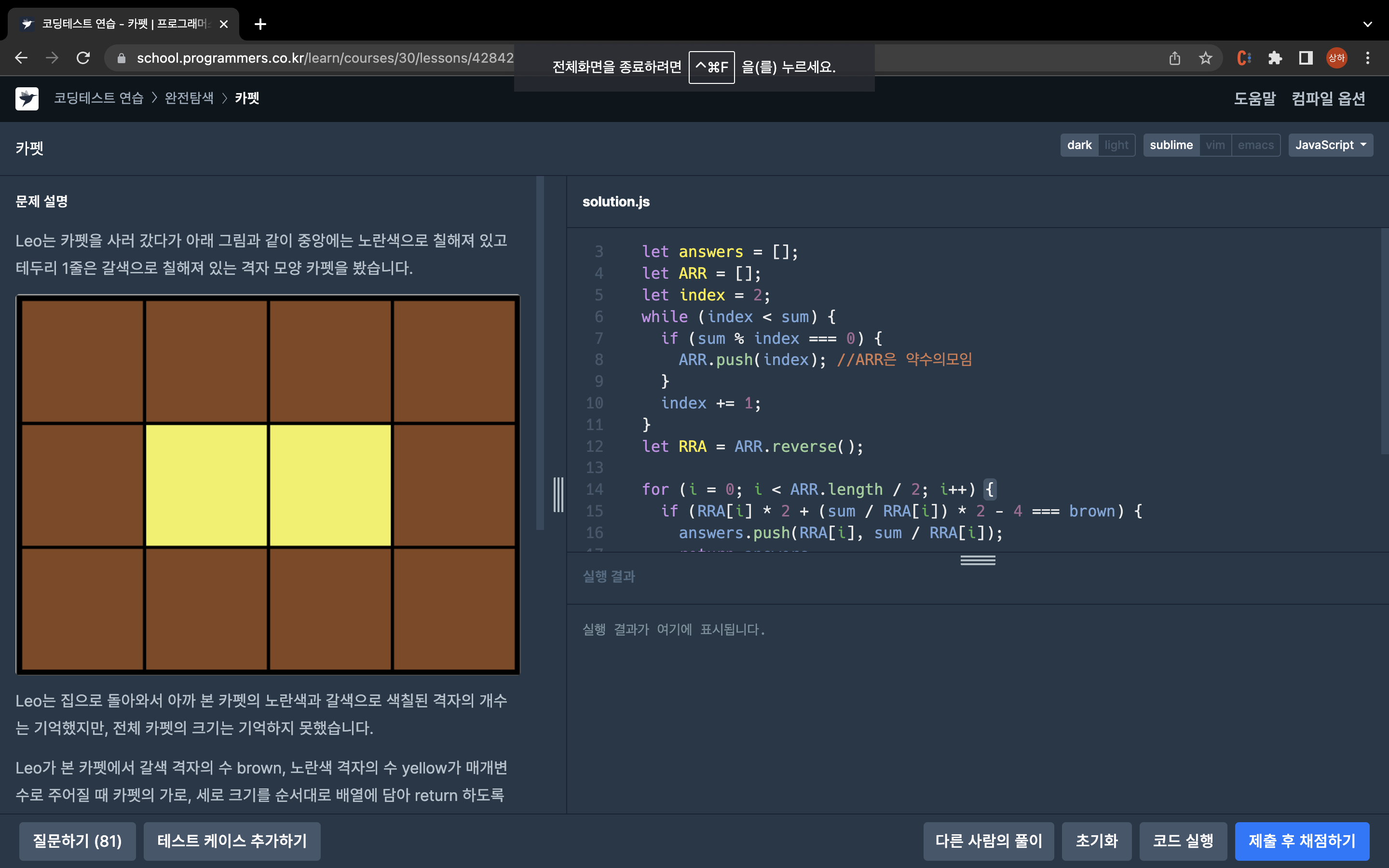
카펫
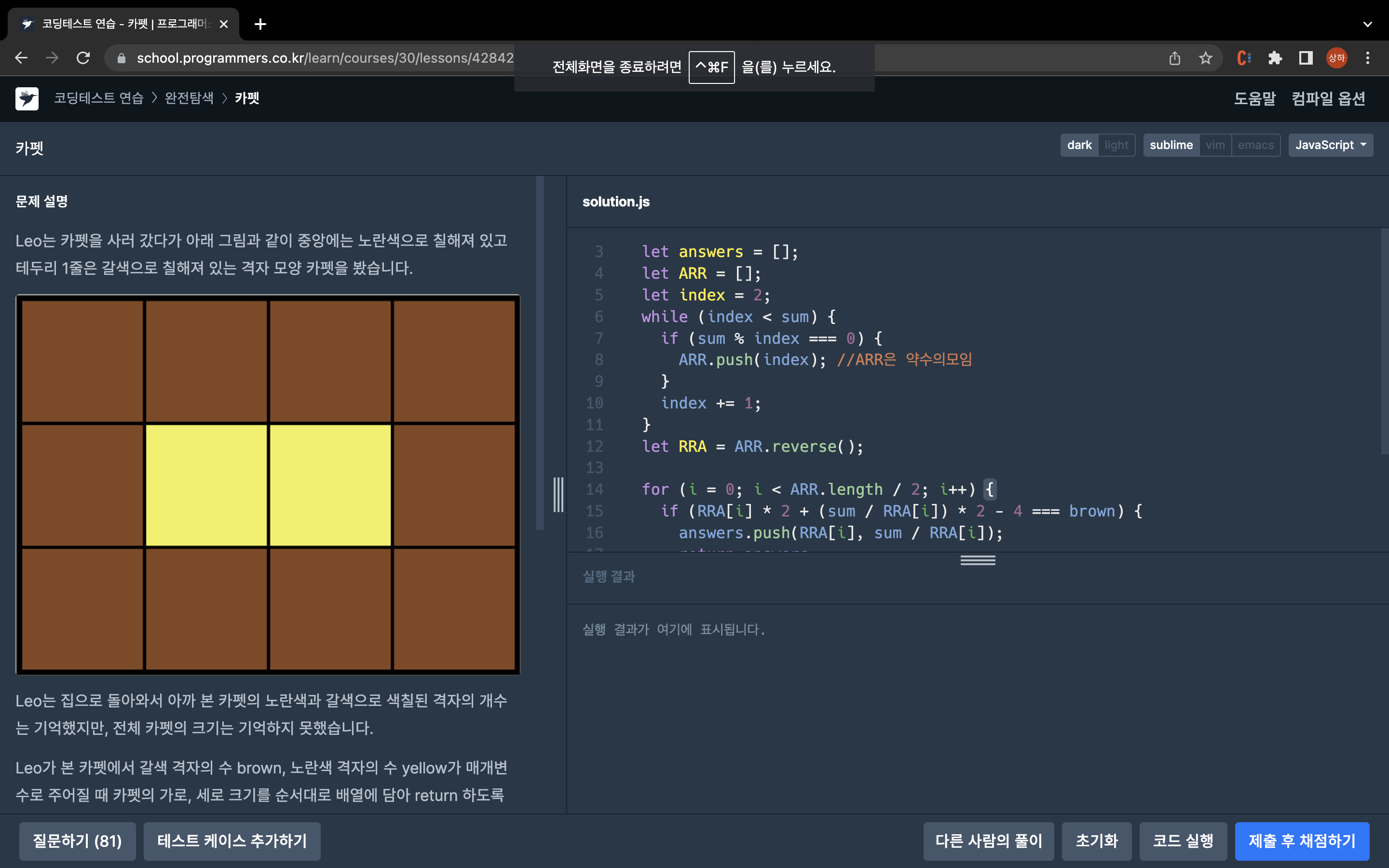
이 문제는 완전탐색 카테고리로 분류되어 있었다. 완전 탐색이란 반복문을 사용하여 말 그대로 경우의 수를 구하는 문제이다.
필자는 이 문제에서 구해야 하는 것은 전체 카펫의 가로길이와 세로길이임을 알고
규칙이 있을 거란 생각을 했다. 내가 발견한 규칙은 다음과 같다.
- x, y를 사용한 연립방정식으로 풀수있겠다.
- 여기서 x는 yellow의 가로길이 y는 yellow의 세로길이이다.
- x+y = (brown-4)/4
- xy = yellow
즉, yellow의 가로길이와 세로길이를 알게 되면 전체 카펫의 가로, 세로길이는
yellow가로 +2 , yellow세로 +2
가 될 것이다!
그렇게 내가 생각한 코드는
function solution(brown, yellow) {
const plus = (brown - 4) / 2;
let x = 0;
let y = 0;
for (let i = 1; i <= plus; i++) {
y = plus - i;
//y = plus-x
if (i * y === yellow) {
//xy= yellow
x = i;
break;
}
}
return [x + 2, y + 2].sort((a, b) => b - a);
}저번 시간에 학습해두었던 let의 재할당에 대한 개념을 사용하니 풀이가 이 전보다 더 간결해진거 같다.
const , let , var에 대한 설명은 (2)에 정리해놓았다.
또, 다른 분들의 코드를 보니 Math.sqrt와 Math.pow를 사용하신 분이 많이 계셔서 이 두 메서드에 대한 정리를 해보았다.
Math.sqrt
위 메서드는 number 에 루트를 씌워주는 메서드이다.
사용법은 다음과 같다.
console.log(Math.sqrt(36))
//return 6
Math.pow
위 메서드는 number에 제곱근을 시켜주는 메서드이다.
사용법은 다음과 같다.
console.log(Math.pow(2,3))
//return 8예상대진표
예상 대진표 문제는 그냥 월드컵에서 D조에 있는 팀을 몇번째에 만날 수 있나!!
이 말과 동일했다. 최근 월드컵을 보면서 혼자 생각을 해본적이 있어서 로직을 더 쉽게 짤 수 있었다.
저번에 풀었을 때는 사실 해결하지 못해 질문하기에 있는 답을 긁어왔던 기억이 난다.
이번에는 좀 더 생각을 해보니 다음과 같은 logic을 생각할 수 있었다.
1,2 3,4 5,6 7,8
위 모두 조로 생각을 했을 때 1조 2조=> 1조로, 3조4조는=> 2조로 5조6조 => 3조, 7조8 => 4조로
결국 이건 2로 나눈 몫에 올림을 한 결과같이 같아야 경기때 만나는 구나 라고 생각을 했다.
let n = 8;
let a = 4;
let b = 7;
function solution(n, a, b) {
let count = 0;
while (true) {
a = Math.ceil(a / 2);
b = Math.ceil(b / 2);
count = count + 1;
if (a === b) {
return count;
}
}
}다른 분들의 코드도 위와 같은 로직으로 해결을 했다!!🔥🔥🔥
N개의최소공배수
위 문제는 배열로 숫자가 주어졌을 때 이 들의 최소 공배수를 구하면 된다.
결국, 가장 큰 수를 나머지 배열원소로 나누었을 때 모두 나머지가 0일 때 그때의 가장 큰 수의 배수가
최소 공배수가 된다.
logic은 다음과 같다.
- 배열의 최대값을 꺼내온다. (Math.max 함수를 이용)
- 최대값을 제외한 하나의 배열을 만든다.
- 만든 배열을 순회하며 최대값을 나눈다.
- 나머지가 0이 아닌게 있다면ㅁ 최대값에 최대값을 더 한후 처음부터 순회한다.
- 만약 모두 나머지가 0이라면 그때의 최대값을 리턴한다.
function solution(arr) {
const Max = Math.max(...arr);
let plusMax = Math.max(...arr);
//한 번 더 같은 값을 다른 변수에 저장한 이유는
//plusMax는 계속 변해야하지만 Max값은 고정되어야하기때문이다.
let check = [];
const filterArr = arr.filter((item) => item !== Max);
// 최대값을 제외한 하나의 배열을 만든다.
while (true) {
check = filterArr.filter((item) => plusMax % item === 0);
//for문으로 i를 리셋하는 형식으로하면 더 효율을 높일 수 있을 거 같다.
if (check.length === filterArr.length) {
return plusMax;
}
plusMax = plusMax + Max;
}
}점프와순간이동
위 문제는 규칙성을 찾는게 중요해 보였다.
처음에는 순간이동 하는게 연료가 안든다면 계속 순간이동하면 되지않나? 이렇게 생각했었는데
문제에서는 현재 위치 X2 이라고 했다. 그렇다면 이동한 거리 X2 인데 문제는 얼마나 점프를 해야하나였다.
결론은 이렇다. 어쨋든 점프는 최소 1번은해야한다. 그래야 그 거리만큼 이동할 수 있기 때문
그렇다면 n을 2로나누다가 나머지가 1이되는 시점이 점프를 해야하는 시점이 아닐까?
만약 10이라는 거리를 간다고 생각을 하면 한 칸 이동 후 두배를 가면 현재 위치는 2
한 번 더 두배를 가면 현재 위치는 4 여기서 1만큼 점프하면 현재위치는 5 그리고 순간이동으로 10 위치에 도달 할 수 있다.
내가 발견한 규칙성은 계속 2로 나누다 나머지가 1인 시점이 바로 점프를 해야하는 타이밍이다.
그럼 방법은 두 가지가 있다.
- n이 1이 될 때까지 n을 2로 계속 나누다가 나머지가 1인 시점에서 n에 -1을, jumpcount+1 해주고 이어 반복하기
- n이 1이 될 때 까지 n을 2로 계속 나누다가 나머지가 1인 시점에서 jumpcount+1 해주고 반복하기
나는 2 번의 방법을 채택하였다.
function solution(n) {
if (n === 1) {
return 1;
}
let jump = 1;
while (n !== 1) {
if (n % 2 !== 0) {
jump = jump + 1;
}
//이걸 그냥 n%2를더해줘버려도된다.
n = Math.floor(n / 2);
}
return jump;
}나머지가 0 이 아닌 시점에서 jump 카운트를 높이고 n은 2로 나누어주는데 이때, 몫이 정수가 아닐 수 도 있음으로
소수점(나머지)는 버려준다.
그런데 다른 분의 코드를 보고 더 나은 방법이 있다는 걸 알게됐다.
function solution(n) {
if (n === 1) {
return 1;
}
let jump = 1;
while (n !== 1) {
jump = jump + n%2;
//굳이 if문을 쓰지 않아도 된다.
// 나머지가 0 이라면 그냥 더해주자.
n = Math.floor(n / 2);
}
return jump;
}