코딩테스트의 중요성을 절실히 깨달았다. 코딩테스트를 통과하지 못하면 나의 개발 수준을 궁금해하지 않는다.. 기회를 얻으려면 코딩테스트를 통과하는 게 우선이다. 12개의 알고리즘을 다음과 같이 정리해 나갈 것이다. 
위 알고리즘을 1바퀴 돌리기 위해서는 대략 1달이 걸릴 거 같다. 꾸준히 해나가서 알고리즘 실력을 충분히 올릴 수 있기를 ..! 🔥 꾸준히 해나가면 분명 좋은 기회가 있을 것이다!!
해시
코딩테스트를 풀면서 해당 알고리즘을 깊게 공부해본 적은 없는 거 같다. 얼마 전 멘토와의 상담에서 알고리즘을 알고 문제를 푸는 것과 대략 알고 푸는 것의 차이는 크다고 하셨다. 알고리즘에 대한 학습을 선행하고 그 후 문제를 푸는 방식을 해나갈 것이다.
해시란 ❓
해시 알고리즘은 쉽게 말해 전화번호부와 같다.
이름: 010-xxxx-xxxx
이름: 010-xxxx-xxxx
이름: 010-xxxx-xxxx
이름: 010-xxxx-xxxx
위 처럼 key - value 형태의 자료구조를 해시테이블 이라고한다.
그럼 이렇게 해시 알고리즘을 사용했을 때 장점은 무엇이 있을까
일반 배열과 비교가 가능하다.
[한국,일본,중국,미국,영국] 의 배열이 있을 때 배열에 미국이 포함되어있는지 아닌지를 알기 위해서는 보통은 배열 전체를 탐색해야한다.
for문을 이용해서 미국의 존재 유뮤를 파악해야한다. 그렇지만 Hash 알고리즘의 경우 미국만을 검색이 가능하다는 점이다. 즉 미국을 타겟으로 해시 테이블에 유무를 판단할 수 있어 시간 복잡도에서 유리하다.
데이터는 => 해시함수 => 해시테이블에 넣게 된다.
해시함수 ❓
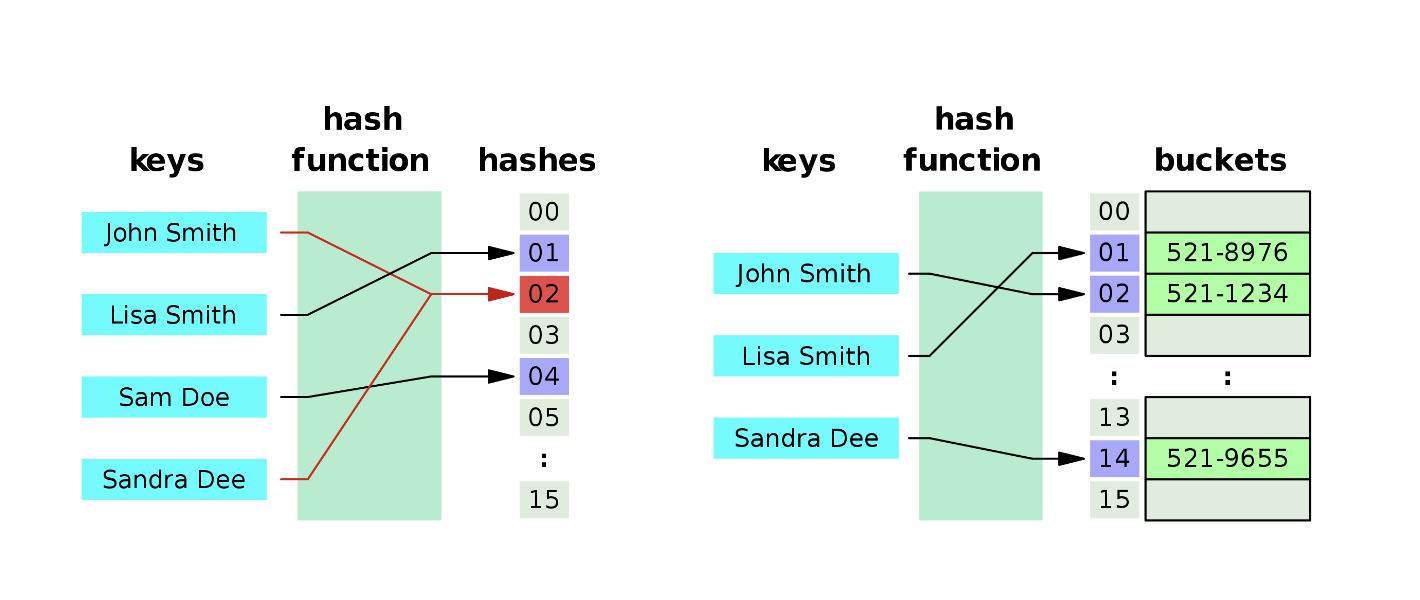
위 그림과 같이 표현이 가능하다.
즉, 임의의 길이를 갖는 임의의 데이터를 고정된 길이의 데이터로 매핑하는 함수 =>고유한 인덱스를 만들어준 후 데이터와 맵핑 해주는 함수
그렇다면 언제 사용할까 ❓
String을 기반으로 정보를 기록하고 관리할 때 !
배열은 Index가 양의 정수로 이루어진다. 그렇지만 해시는 string의 형태로 생성될 수 있다.
문제 적용
해시 알고리즘을 공부하며 프로그래머스에서 제공하는 문제 중 해쉬 알고리즘의 카테고리를 풀고 싶었는데 이미 모두 풀어 본 문제라서 계속 문제를 찾았다.
위 해시 알고리즘에선 찾지 못했고 카카오 2021년 블라인드 채용에 출제된 문제를 발견했다. 위 문제는 재귀함수와 해시를 이용해서 문제를 풀 수 있을 거 같았다.
메뉴 리뉴얼 ❓
위 문제는 먼저 주문이 담긴 배열이 주어진다
["ABCFG", "AC", "CDE", "ACDE", "BCFG", "ACDEH"]
그럼 주문에서 많이 등장한 메뉴를 course의 수에 맞게 찾으면 된다.
AC는 총 4번 등장한다. 그럼 AC는 2가지 메뉴를 넣은 코스의 대표 메뉴가 되는 것이다.
이렇게 각 배열의 원소를 course만큼 나누어 해당 원소가 다른 배열 원소에 포함되어있는지 만약 포함된다면 몇번 포함되는지를 알아봐야한다.
이 부분에서 재귀함수와 해시가 필요하다고 느꼈다. 먼저 각 주문으로 만들 수 있는 메뉴의 종류는 재귀함수로 뽑아내고 만들어진 메뉴의 종류를 해시를 이용해 count하는 것이다.
이 문제를 푸는데 2일이 걸린 거 같다.. 그래도 결과는 ! 
성공이었다.
지금부터 내가 쓴 코드를 분석하고 다른 사람의 코드를 살펴보도록 하겠다.
function solution(orders,course){
for(let i = 0 ; i <orders.length; i++){
let visited = Array.from({length:oreders[i].length},()=>false)
const dfs=(sum,course,visited)=>{
for(let j=0; j<orders[i].length; j++){
if(sum.length===course){
//이 부분에서 sum이 생긴다.
return ;
}
if(visited[j]===false){
visited[j]=true;
//방문
dfs(sum+orders[i][j],course,visited)
//탈출
visited[j]=false
}
}
}
for(let k=0;k<course.length;k++){
dfs(``,course[k],visited)
}
}
//각 order에 따라 가능한 조합을 모두 만들어야 하기 때문에 이 반복문 안에서 dfs를 만들어준다.
}위 함수는 일단 겹치지 않는 sum의 즉, course에 맞는 메뉴의 구성 종류와 같다.
이렇게하면 모든 메뉴의 구성을 받아올 수 있다. 그럼 이제 몇번 나왔는지만 체크할 수 있으면 되지 않겠는가?
하지만 여기서 문제가 있다.
바로 AB와 BA를 구분 짓는 다는 점. 순서는 상관하지 않고 AB와 BA를 같은 것으로 봐야하는데 여기선 다른 것으로 봐서 Sum을 저장할 때 어려움이 있다.
이 글을 쓰면서 생각했는데 그냥 차라리 한번에 받고 sort를 이용한 후 중복을 제거하는 것도 나쁘지 않겠다고 생각이 든다.
필자는 아직 투포인터를 학습하지 않아 나름의 방법을 생각했다.
for (let i = 0; i < orders.length; i++) {
let visited = Array.from({ length: orders[i].length }, () => false);
let startIndex = 0;
const dfs = (sum, course, visited) => {
for (let j = 0; j < orders[i].length; j++) {
startIndex = orders[i].indexOf(sum[sum.length - 1]);
// 현재 더해진 Index보다 더 뒤에 것만 더할 수 있도록 해야함
if (sum.length === course) {
return;
}
if (visited[j] === false && j >= startIndex) {
visited[j] = true;
dfs(sum + orders[i][j], course, visited);
visited[j] = false;
}
}
};
for (let k = 0; k < course.length; k++) {
dfs(``, course[k], visited);
startIndex = 0;
}
}예를 들어 AB를 더했고 C를 더할 차례다 하면 AB에서 B는 Index 1이다 그럼 j가 1보다 큰 경우만 더해질 수 있도록 한 것이다.
만약 [ACBE]라는 order가 있을 때 지금 현재 CB를 더한 sum이 있다면 A를 추가로 더해 CBA가 나올 수 없게 만드는 것이다. 이미 ABC가 순차적으로 이전에 더해졌을 거기 때문이다.
그럼 이제 메뉴를 만드는 건 가능해졌다. 그럼 가장 많이 나오는 메뉴를 어떻게 뽑을 수 있을까?
이 부분을 Hash를 사용했다. string을 이용해 key-value의 형태로 저장하는것!
for (let i = 0; i < orders.length; i++) {
let visited = Array.from({ length: orders[i].length }, () => false);
let startIndex = 0;
const dfs = (sum, course, visited) => {
for (let j = 0; j < orders[i].length; j++) {
startIndex = orders[i].indexOf(sum[sum.length - 1]);
if (sum.length === course) {
if (!menuList.includes(sum)) {
// 이 부분은 수정해도 될거 같다. 그냥 menuHash.get(sum)===undefined이면
// set하도록!
menuList.push(sum);
menuHash.set(sum, 1);
} else if (menuList.includes(sum)) {
if (menuHash.get(sum) !== undefined) {
menuHash.set(sum, menuHash.get(sum) + 1);
}
}
return;
}
if (visited[j] === false && j >= startIndex) {
visited[j] = true;
dfs(sum + orders[i][j], course, visited);
visited[j] = false;
}
}
};
for (let k = 0; k < course.length; k++) {
dfs(``, course[k], visited);
startIndex = 0;
}
}위 처럼 하면 course에 따른 각 메뉴를 전체적으로 count할 수 있다. 첫 번째 order의 course 1,2,3 을 모두 체크하여 없다면 hash로 저장하고 또 다음 order에서도 course 1,2,3(길이)에 따라 hash로 저장하기 때문에 최종적으로 count된 key-value를 얻을 수 있다. 이제 위 받아온 해쉬를 크기순으로 정렬하여 가장 많이 count되고 그 값이 2보다 큰 메뉴를 answer에 push하면된다.
최종적인 코드는 다음과 같다.
function solution(orders, course) {
const answer = [];
let menuList = [];
let menuHash = new Map();
orders = orders.map((item) =>
item.split(``).sort((a, b) => (a > b ? 1 : -1))
);
for (let i = 0; i < orders.length; i++) {
let visited = Array.from({ length: orders[i].length }, () => false);
let startIndex = 0;
const dfs = (sum, course, visited) => {
for (let j = 0; j < orders[i].length; j++) {
startIndex = orders[i].indexOf(sum[sum.length - 1]);
if (sum.length === course) {
//이건 이제 등록이 된거잖아
// 뒤로 더하는 걸로하면될듯
if (!menuList.includes(sum)) {
menuList.push(sum);
menuHash.set(sum, 1);
} else if (menuList.includes(sum)) {
if (menuHash.get(sum) !== undefined) {
menuHash.set(sum, menuHash.get(sum) + 1);
}
}
return;
}
if (visited[j] === false && j >= startIndex) {
visited[j] = true;
dfs(sum + orders[i][j], course, visited);
visited[j] = false;
}
}
};
//여기서 dfs를 실행해주어야함 2,3,4인경우를 모두 비교해야하니까
for (let k = 0; k < course.length; k++) {
dfs(``, course[k], visited);
startIndex = 0;
}
}
menuHash = [...menuHash];
menuHash
.sort((a, b) => a[0].length - b[0].length)
.sort((a, b) => b[1] - a[1]);
for (let k = 0; k < course.length; k++) {
let arr = menuHash.filter((item) => item[0].length === course[k]);
arr = arr.filter((item) => item[1] === arr[0][1] && item[1] >= 2);
arr.forEach((item) => answer.push(item[0]));
}
return answer.sort();
}해쉬는 오히려 많은 반복을 줄여준다. 위 문제를 푸는데 꽤 오려걸렸는데 그만큼 또 찐하게 배운 거 같다.
이제 다른 사람의 코드를 찾아보겠다.
조합을 구하는 다른 방법이 ❓
const getCombinations = (array, selectNumber) => {
const results = [];
if(selectNumber === 1){
return array.map((element) => [element]);
}
array.forEach((fixed, index, origin) => {
const rest = origin.slice(index+1);
const combinations = getCombinations(rest, selectNumber - 1);
const attached = combinations.map((combination) => [fixed, ...combination]);
results.push(...attached);
});
return results;
}
console.log(getCombinations([1,2,3,4], 3));위 코드는 조합을 구하는 다른 방법이다.
필자가 구하는 방법은 재귀와 stack을 이용하여 조합을 구현했었는데 위와 같은 방법이 있다는 것을 알게 되었다. 다른 분들도 보통 위와 같은 방법으로 메뉴경우를 구하셨다.
나머지는 거의 비슷한데 위 메뉴의 경우를 구하는 방식에서 차이가 났다.
재귀함수과 stack을 활용하는 방법도 좋지만 위 Combination 함수를 알고 있으면 더 좋을 거 같다.

