알고리즘 정복기 - 이분탐색/투포인터

박상하·2023년 6월 13일

코딩테스트

목록 보기

20/37

이분탐색/투포인터

오늘은 이분탐색/투포인터에 대해 학습을 해보겠다..!

이분탐색을 타이틀로 하는 프로그래머스 문제 유형이 있었지만 위와 같은 알고리즘을 사용해서 풀지 않았던 거 같다.
그렇다면 이분탐색과 투포인터는 무엇이며 서로 다른 것일까?
지금부터 알아보자!!

이분탐색/투포인터 블로그

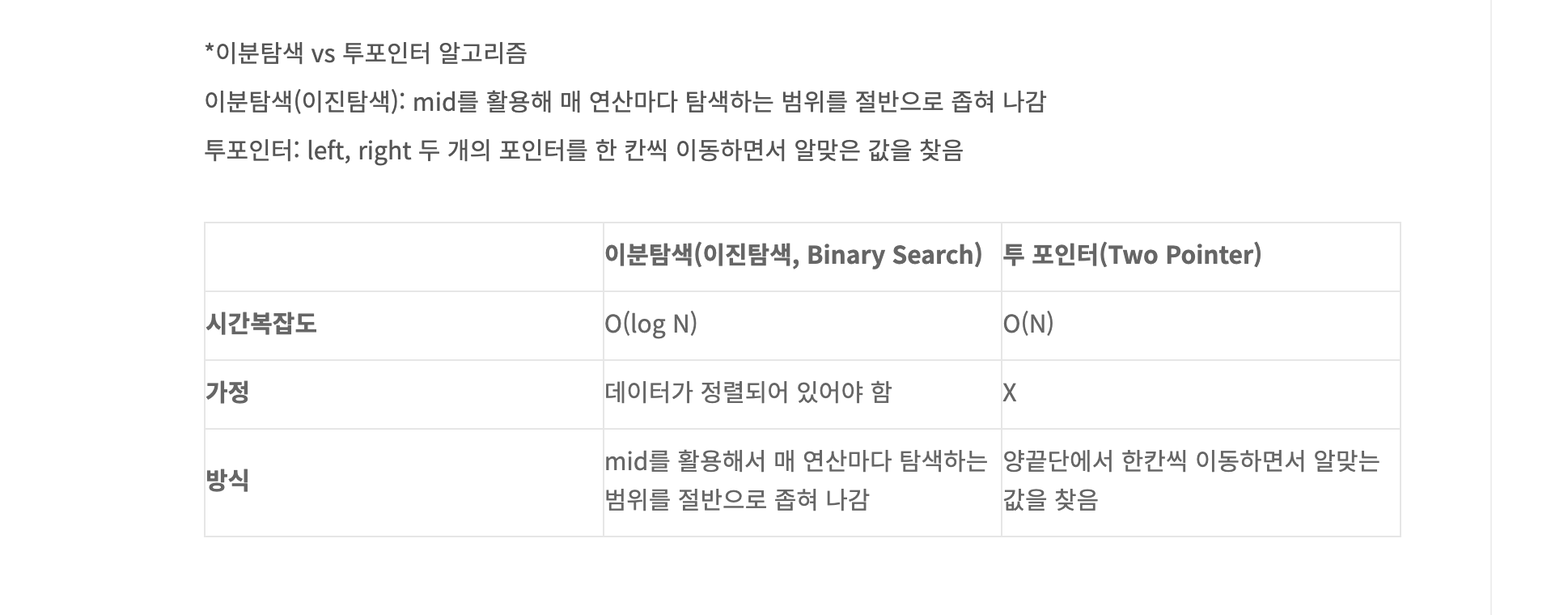
다음 사진은 위 블로그에서 발췌해왔다.

이분탐색 ❓

이분 탐색은 쉽게 말해 절반으로 쪼개가며 원하는 값을 찾는 방식이다.

위 사진 처럼 Mid를 기준으로 값을 찾는데
start와 end의 기본 set은 각각 0 , length-1이 된다.

그 후 mid는 (start+end)/2 가 되는데 홀수인경우 Math.floor 메소드를 활용해주면 된다.

mid와 target을 비교하며 만약 target이 mid보다 작다면? ( target<mid)

end를 움직여줘여한다. mid = end-1

만약 target이 mid보다 크다면? (target>mid)

start를 움직여줘야한다. mid = start+1

그렇게 mid를 계속 변경하며 해당 값을 찾아나갈 수 있다.

즉 절반으로 나눠가는 탐색

이분탐색은 원하는 추정 값의 범위를 좁힐 때도 사용이 가능할 거 같다.

투포인터 ❓

투포인터는 그냥 포인터가 2개인 것이다. 즉, 두 개의 손가락으로 배열을 짚어가는 거라 생각하면 좋다. 보통 배열의 원소의 합이 6인 두개의 원소를 총 경우를 구할 때 사용할 수 있을 것이다.

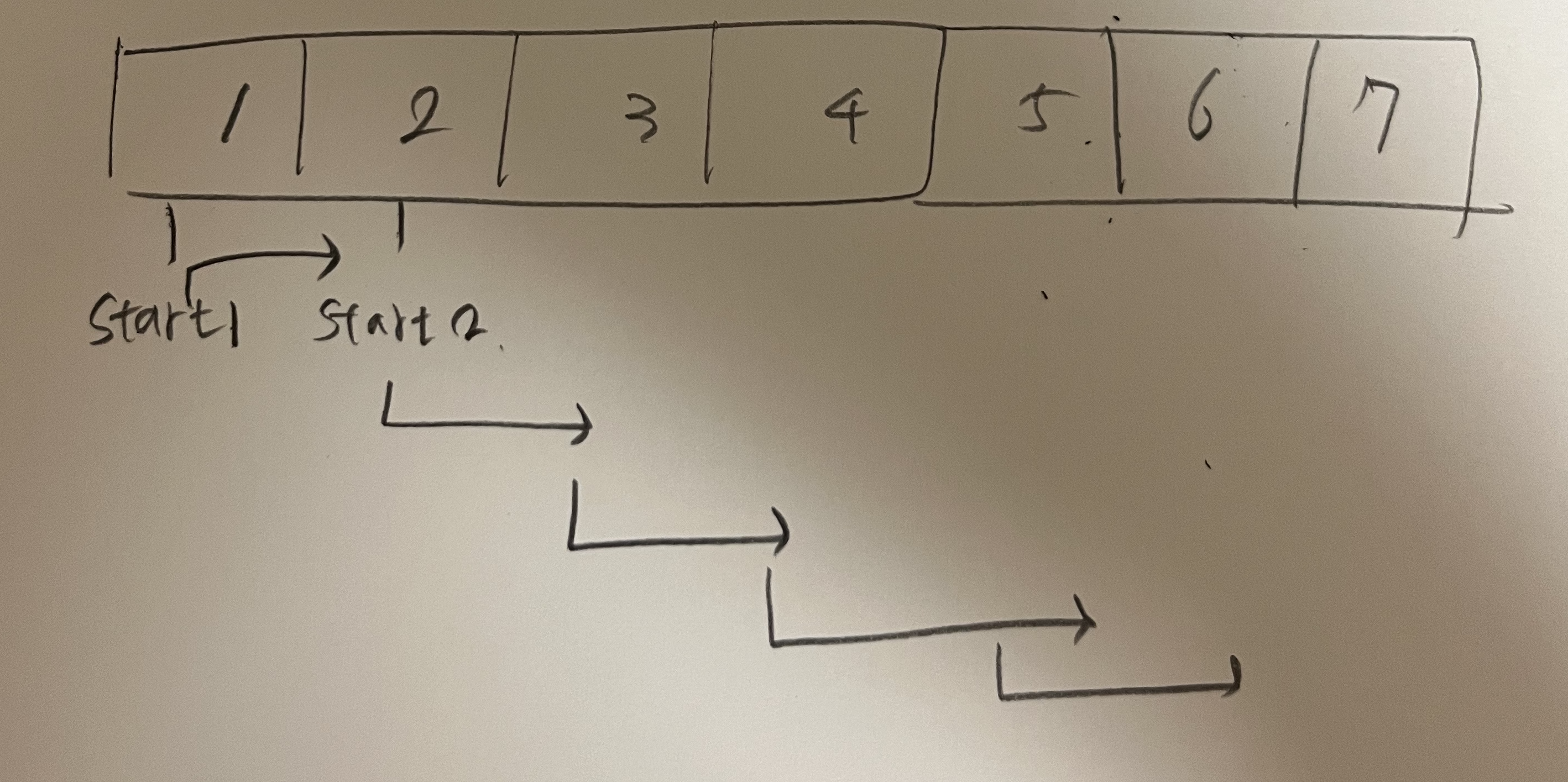
이런식으로 포인터 1 은 고정 포인터 2가 이동하며 어떤 조건이 충족하면 포인터 1을 옮겨가며 원하는 값을 구할 수 있다. 이는 완전탐색에서 효율성 검사가 실패할때 사용하면 좋은 방법이라고 한다.

또, 포인터가 start와 end에 두고 mid쪽으로 좁혀가며 값을 세어볼 수도 있다.

문제적용 (연속된 부분수열) ❓

투포인터

위 문제를 풀기 전까지는 제대로 투포인터에 대해 이해하지 못했던 거 같다. ~~(문제를 푼 지금 시점에서 보니 그렇다..)~~

일단은 잘못생각했던 부분을 먼저 적어보겠다.

나의 착각 ❓

투포인터를 다음과 같이 이해했었다.

[1, 2, 3, 4, 5, 6, 7] 의 배열이 있다면
start=0
end=start+1에서 가서 만약 target보다 크다면?? start를 옮겨주고 또 end도 start+1부터 시작하는거구나??

근데 이렇게 생각해보면 결국은 완전탐색과 다를게 없지 않는가!!
결국 다 살펴보겠다는 건데 그러면 for 반복문을 중첩해서 사용하는게 낫겠다..
문제를 풀어보면서 알게되었다. 투포인터에 대해 더욱 깊게!

그럼 투포인터를 어떻게 이해해야하나??

설명이 될지 모르겠으니 글로 한 번 더 설명을 해보겠다.

[1, 2, 3, 4, 5, 6, 7] 의 배열에서 start를 0으로 출발했다면
end도 똑같이 0이 된다. 그렇게 sum = arr[start]가 되는 것이고 만약 이 sum의 값이 target보다 크냐 작냐에 따라 start와 end를 조절해주는 것이다.
만약 sum< target 이라면??
최근의 start는 삭제하고 start를 오른쪽으로 한칸 옮겨준다.
만약 sum> target 이라면??
end를 한칸 높여주고 sum에 arr[end]를 더해준다.

위 문제에서 이분탐색을 사용해야하는 이유는 3가지가 있다.

sort되어져있다는 게 이 문제의 힌트
=> 이분탐색 알고리즘을 사용하려면 sort(정렬)해야 사용이 가능하다.
이는 외우지 않아도 생각해보면 왜 그런지 알 수 있다. start와 end를 각 상황에 맞게 증가시킬 수 있는 것은 수가 정돈 되어 있기 때문에 가능한 것이다.
연속된 부분수열을 찾는 문제이기 때문
=> 이분탐색 알고리즘은 연속된 합을 구할 때 좋다. 왜냐하면 더해가다가 target보다 크다면 start를 +1 높이고 작다면 end를 +1 높일 수 있는 이유는 연속된 수열일 경우에 가능하다. 만약 연속적이지 않고 부분수열을 찾는 문제라면 오히려 완전탐색을 해야 가능할 것이다.
시간복잡도에서 유리하다.

이 문제와 알고리즘을 학습하며 가장 크게 배운 점은 시간복잡도이다. 이를 계속 공부해야지 생각만 하고 미뤄뒀었는데 이번 기회에 정리를 할 수 있었다.

노마드코더 시간복잡도
개발남노씨 시간복잡도
개발남노씨 코딩테스트 공략법

위 유튜브 영상을 가장 많이 참고하여 학습하였다.

시간복잡도 ❓

시간복잡도는 쉽게 말해 이 문제를 푸는데 몇 단계를 거치니? 이다
이 몇 단계를 표시할 수 있는 방법 중 하나는 Big-O 표기법이고 이를 보편적으로 많이 사용한다. 그렇다면 Input이 N인데 N단계를 거치는 알고리즘은 ??
어떤 시간 복잡도를 가질까?

바로 Big-O(N)이다. 왜일까? 코드로 살펴보자

const arr =[1,2,3,4,5]
//n =5
const print=()=>{ 
for(let i = 0 ; i<arr.length; i++){
 console.log(arr[i)) 
}
}
//N번 순회하면 console을 찍기 때문에 print함수는 Big-O(N)의 시간복잡도를 갖는다.

이중 반복문은 어떨까?
Input이 N인 반복문을 2번 돌리기 때문에 Big-O(N^2)이 된다.

그럼 가장 빠른 시간복잡도는 무엇일까? 바로 O(1)의 시간복잡도이다.
이는 상수시간 알고리즘이라고하며
=> Input과 관계없이 Step이 정해진다.

이전에 배웠던 Hash를 사용하면 시간복잡도가 1 이라는 설명이 있었는데 이제 이해가 된다.

Hash는 Key-value의 자료구조로 원하는 Value의 key를 호출하면 Value를 가져다 준다.

const Obj ={
 name:"Updownpark" 
}
const print=()=>{
 console.log(Obj.name) 
}

위 함수는 O(1)의 시간 복잡도를 갖는다. Obj의 길이가 얼마나 길든 상관없이 print는 원하는 key를 1번만 호출하여 값을 가져올 수 있다.

그렇다면 투포인터 알고리즘의 시간복잡도는 어떻게 될까?

결론부터 말하자면 O(N)의 시간복잡도를 갖는다.

왜냐하면 while 반복문 안에서 최대 N번 순회하기 때문이다.

이분탐색의 시간복잡도는 어떻게 될까?

이것도 결론부터 말하자면 O(logn)의 시간복잡도를 갖는다.

이분 탐색은 N의 인풋을 절반으로 자르고 계속 자르지않는가. 그렇게 때문에 지수와 상관관계에 있는 logN의 시간복잡도를 갖는데 아직 100% 이해하지 못해 글로써 제대로 설명이 불가능할 거 같다. 차후에 시간복잡도에 대한 내용을 따로 빼 정리할것이다. 알고싶은분은 저기 위 유튜브를 보면 아주 잘나와있다.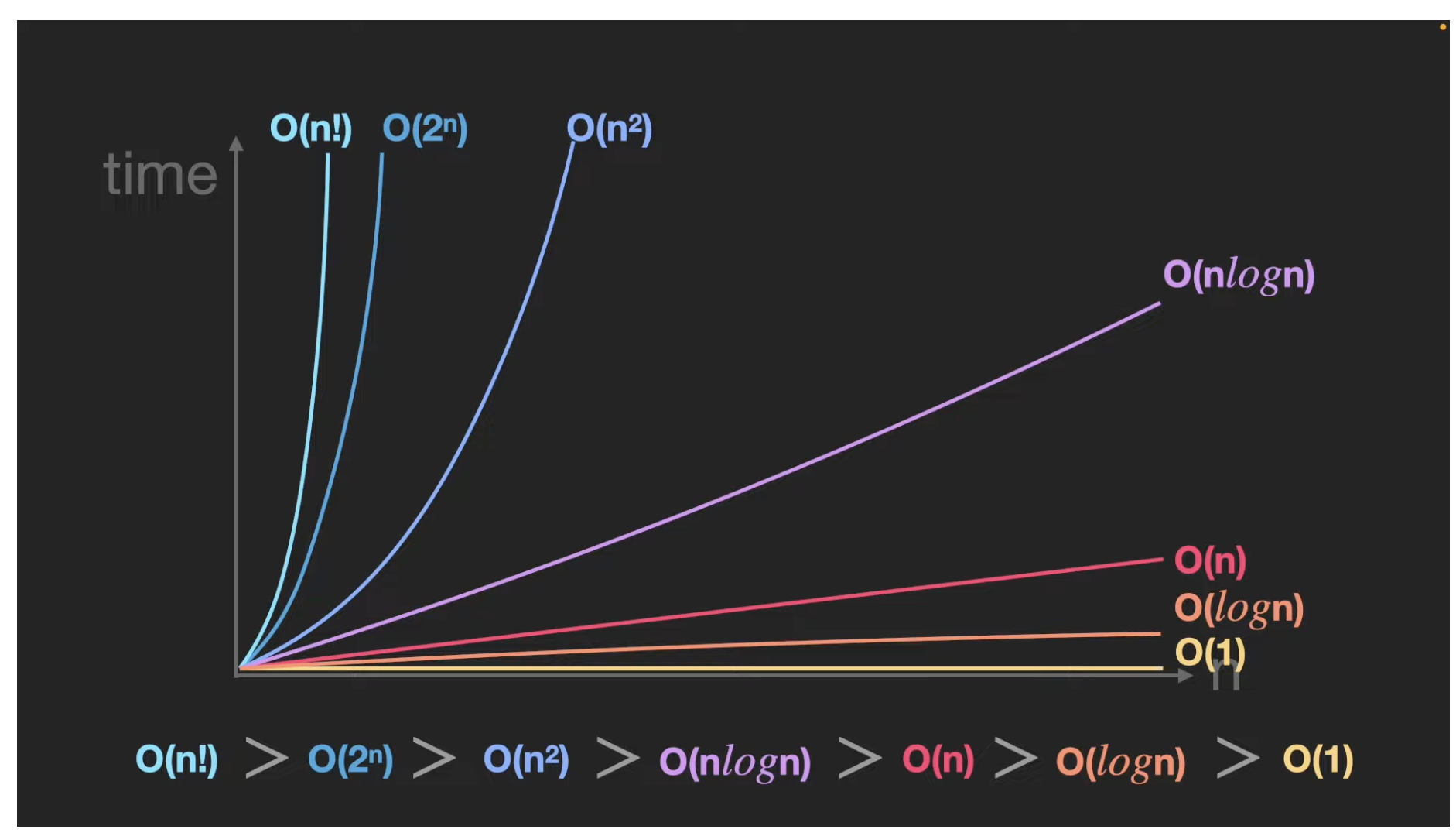

코딩테스트에는 복잡도(N이) 1억이 넘으면 안돼 ❓

코딩테스트를 보며 다양한 Input의 범위를 봐왔지만 시간복잡도를 계산하며 주의깊게 살펴보지 않았었다. 모든 문제는 Input과 그 범위가 존재한다. 원하는 값을 return할때 그 단계가 1억번을 넘기지 않도록 코드를 구성해야하는 것이다. 이 점을 이제 알고 코드를 짠다면 시간초과라는 찬물에 들어갈 확률은 좀 줄어들지 않을까?

다시문제로 ❗️

처음 필자가 짠 코드는 다음과 같다.

   function solution(sequence, k) {
  let start = 0;
  let end = 0;
  let length = 123123123123;
  let answer = [];
  let sum = sequence[start];
  if (sum === k) {
    return [0];
  }
  while (sequence[start] <= k) {
    console.log(sum, start, end);
    if (sum === k) {
      if (end - start < length) {
        length = end - start;
        answer = [start, end];
      }
      start = start + 1;
      sum = sequence[start];
      end = start;
    } else if (sum > k || end === sequence.length) {
      start = start + 1;
      end = start;
      sum = sequence[start];
    } else {
      end = end + 1;
      sum = sum + sequence[end];
    }
    if (start === sequence.length) {
      return answer;
    }
  }
  return answer;
}
// 시간 초과1

하하하!! 굉장히 지저분하고 심지어 투포인터 알고리즘도 잘못사용하고있다. 이건 그냥 이중반복문이잖아!! (굉장히 복잡하게 만든)

다음 코드는 조금 더 간결해졌지만 로직은 비슷하다.

function solution(sequence, k) {
  let start = 0;
  let end = 1;
  let sum = sequence[start];
  let answer = [];
  let length = 1000010;
  while (start < sequence.length) {
    if (sum >= k || end - 1 === sequence.length) {
      if (sum === k && length > end - 1 - start) {
        // 해를 찾았을 때
        answer = [start, end - 1];
        length = end - 1 - start;
      }
      start = start + 1;
      end = start + 1;
      sum = sequence[start];
    } else if (sum < k) {
      sum = sum + sequence[end];
      end = end + 1;
    }
  }
  return answer;
}
// 시간 초과2

이후 골머리를 앓은 후 제대로 투포인터를 이해하고 코드를 작성할 수 있었다.

let suquence = [1,2,3,4,5]
let k = 7

function solution(sequence,k){
 let start =0
 let end =0
 let answer =[]
 let sum = sequence[start]
 
while(end===sequence.length){
 //종료조건 => end가 끝까지 왔다는 건 더 이상 더할 게 없다는 거
 //모든 경우를 따져봤다는 것
 if(sum>k){
  sum=sum-sequence[start]
   // sum에서 최근의 start를 버리고 
  start=start+1
   // 새로운 start로 지점을 옮겨준다.
 }
  else if(sum<k){
  end=end+1
    //end를 한 칸 옮겨주고
  sum=sum+sequence[end]
    // sum에 sequence의 end 인덱스를 더해준다.
  }
  else if(sum===k){
   //같다면?
    answer.push([start,end])
    // answer에 push해주고(예비 answer)
    sum=sum-sequence[start]
    // sum에서 최근 start를 제거하고 다시 새롭게 찾아본다.
    start=start+1
  }
}
  answer.sort((a, b) => (a[1] - a[0]) - (b[1] - b[0]))
  // end-start의 길이가 짧은 순서대로 정렬한다.
  // 이때 중괄호를 잘 생각하자
  return answer[0]
}