TIL - 2024/04/05

박상우·2024년 4월 6일

TIL

📝 TIL

목록 보기

13/21

FE 아티클 읽기

[번역] 리액트 컴파일러와 리액트 19 - 이제 메모이제이션을 신경쓰지 않아도 되나요?

내용

React 19의 등장 이슈와 함께 거론되고 있는 이슈 중 하나가 React Compiler의 등장이다. React Compiler의 등장이 이슈가 되고 있는 이유는 기존에 React.memo, useMemo, useCallback을 통해서 사용할 수 있었던 메모지에이션을 컴파일러를 통해서 쉽게 관리할 수 있게 되기 때문이다.

React Compiler는 일반적으로 우리가 작성한 리액트 코드에서 모든 훅, 종속성 및 컴포넌트의 프로퍼티, 컴포넌트 자체를 메모화 하여 코드를 변환하는 Babel의 플러그인 역할을 하게 될 것이라고 한다.

React Compiler를 통해서 부모/자식 간 리랜더링, 제대로된 메모지에이션 구현, 기존 리액트에서 컴포넌트를 리랜더링하기 위한 비교(diff)와 재조정(reconciliation)의 변화 등 많은 것들이 변화할 것이고, 이 것들은 리액트 생태계를 더욱 풍부하게 해줄 것이라 기대하고 있다.
Opinion

React 19와 관련된 사설이나 번역 글 들이 많이 올라오고 있다. 매번 버전업이 될 때마다 DX에 많은 변화를 가져오고 있어서 이번 버전업도 기대가 많이된다. 그리고 특히 이번 사설에서도 다룬 React Compiler의 경우 내용처럼 많은 리액트 개발 방식이나 코드들에 변화가 있을 것이라는 생각이들었다. 관련 발표 영상이나 글을 통해서 어떤 키워드들을 더 봐야하는지 알아보고 미리 대비할 필요가 있을 것 같다.

분할 정복 (Divide and Conquor)

문제를 작게 분할한 후 각각을 정복하는 알고리즘.

큰 문제를 작은문제로 나누어(분할) 각각 해결(정복)하고, 그 결과를 결합(결합)하여 전체 문제를 해결한다.

분할 정복 과정

분할 : 현재의 문제와 동일한 현태지만 더 작은 입력크기의 부분 문제로 분할한다.

정복: 각 부분 문제를 재귀적으로 풀어서 정복한다, 부분 문제의 크기가 작은 경우(base case) 직접적인 방법으로 해결한다.

결합: 부분 문제의 해를 결합해 원래 문제의 크기로 만든다.

작은 문제들은 큰 문제와 같은 형태를 가지고, 원래 문제의 일부분이 된다.

분할 정복 알고리즘은 문제의 부분 문제들이 서로 독립적인 경우 사용하기 좋다.

주로 합병정렬, 이진탐색, 퀵 정렬 등에 사용되고 있다.

DP의 경우 Top-Down 방식, Bottom-Up 방식 모두 접근 가능하지만, 분할 정복의 경우 Bottom-Up의 형태로만 문제를 풀게된다.

동적 계획법(DP)와 함께보기

어제 동적 계획법을 보면서 분할 정복과 동적 계획법 사이의 분명한 차이나 두 알고리즘의 범주를 생각해봐야겠다 생각했다.

정리해보면,

두 알고리즘의 공통점은 큰 문제를 작은 문제로 나누고, 작은 문제를 통해 큰 문제를 해결하려는 접근 방식인 것 같다.

그렇다면 두 알고리즘의 차이점은 동적 계획법(DP)의 경우 작은 문제들이 중복되는 형태로 이루어져 있고, 작은 문제의 답을 저장해두고 그 값을 가지고 큰 문제의 답을 계산(?) 만들어낸다.

하지만 분할 정복의 경우 작은 문제들이 독립적인 형태가 되고, 단순히 결과 값을 합치는 과정을 통해 큰 문제를 해결한다.

배낭 문제 (Knapsack Problem)

대표적인 DP 알고리즘 중 하나.

일반적으로, N개의 물건과 배낭이 있고, 각 물건은 가치와 무게가 있고, 배낭은 최대 용량이 존재한다.

이때 가방에 담을 수 있는 최대 가치의 합을 구하는 문제이다.

문제는 크게 물건을 쪼갤 수 있는 Fraction Knapsack Problem과 쪼갤 수 없는 0-1 Knapsack Problem으로 나뉜다.

왜 배낭 문제가 DP인가.

배낭문제를 다음과 같이 보면 조합의 문제처럼 볼 수 있다.

💡 서로 다른 무게와 가치를 가진 물건을 특정 무게 내에서 조합해서 만들 수 있는 가치 값은? (조합은?)

하지만 약간 문제를 다르게 접근해보면 다음과 같이 해석 할 수 있다.

배낭에 x kg의 무게를 넣는다면, 다음 해결해야하는 문제는 x kg 물건을 제외한 (M - x)kg을 담을 수 있는 배낭에 물건을 넣을 때 나올 수 있는 최대의 가치를 계산하는 문제가 된다.

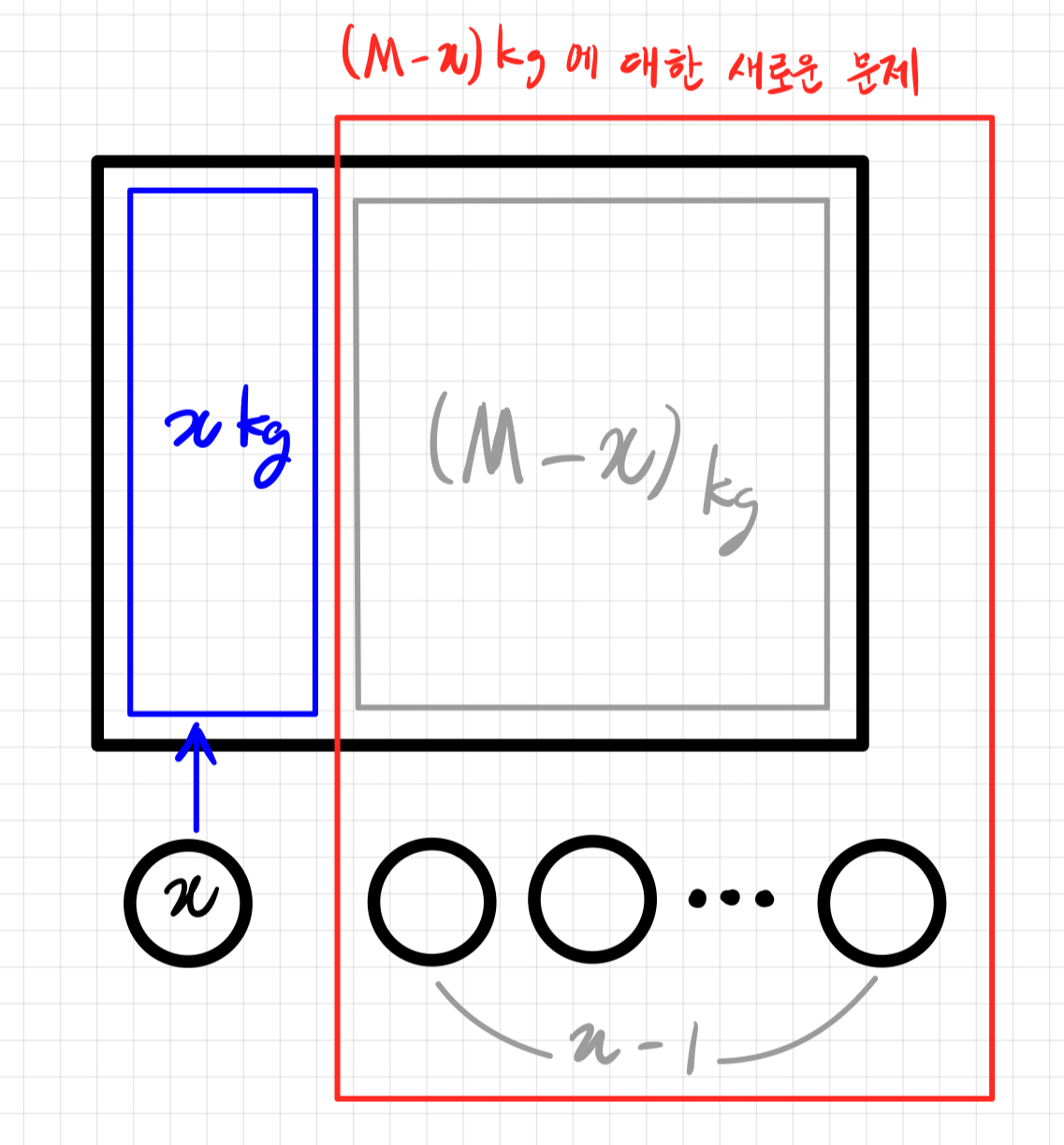
따라서 정리해보면 배낭문제는 물건을 넣을 때마다 남는 공간과 물건에 대해서 새로운 작은 문제들이 파생되는 형태이고, 남은 무게에 따라 물건을 넣는 최적의 방법이 반복되서 사용되기 때문에 배낭 문제를 대표적인 DP 문제라고 보는 것 같다.

식 만들어보기

물건을 넣을때 우선 배낭의 남은 공간에 물건을 넣을 수 있는지 확인해야한다. 그리고 만약 물건을 넣을 수 있더라도 현재 물건을 넣었을 때의 최적의 값과 넣지 않았을 때의 최적의 값을 비교하여 더 큰 가치를 선택해야한다.

아래에서 식으로 확인해보자.

물건을 넣을 수 없을 때,

물건을 넣을 수 없다면 이전 물건까지의 최적의 방법을 가져다 쓰면 된다.
```
bp[i][j] = bp[i-1][j]
```
물건을 넣을 수 있을 때,
- 물건을 넣었을 때 최적의 가치 물건을 넣었을 때의 가치는 현재 넣으려는 물건의 가치와 현재 물건을 넣었을 때 남는 공간에 대한 최적의 값을 합한 가치이다.
```
current_value = V[i]
small_task_value = dp[i-1][j - w[i]]

current_best_value = current_value + small_task_value
```
- i번째 물건을 넣지 않았을 때 최적의 가치 i번째 물건을 넣지 않았을 때의 최적의 가치는 i-1번째 까지의 물건들로 현재의 공간을 채우는 최적의 값을 그대로 사용한다.
```
bp[i-1][j]
```
이제 이 두값 중에 더 큰 값을 최적의 값으로 선택한다.
```
dp[i][j] = max(V[i] + dp[i-1][j - w[i]]), bp[i-1][j])
```

이 부분을 반복해서 작은 값을 특정 데이터 구조에 저장하여 다음 더 큰 무게와 더 많은 물건에 대한 최적의 값을 구할때 사용할 수 있도록 코드를 구성하면 된다.

배낭문제 풀어보자

Link : https://www.acmicpc.net/problem/12865


import sys

input = sys.stdin.readline

N, K = map(int, input().split())

w = []
v = []

for _ in range(N):
  v1, v2 = map(int, input().split())
  w.append(v1)
  v.append(v2)

dp = [ [ 0 ] * ( K + 1 ) for _ in range( N + 1 ) ] # 메모지에이션할 데이터 구조 생성
max_value = 0

for i in range(1, N + 1):
  for j in range(1, K + 1):
    if w[i - 1] <= j:
      dp[i][j] = max(v[i-1] + dp[i-1][j - w[i -1 ]], dp[i-1][j])
    else:
      dp[i][j] = dp[i - 1][j]
    
    max_value = max(dp[i][j], max_value)
  
print(max_value)