TIL - 2024/04/06

박상우·2024년 4월 6일

TIL

📝 TIL

목록 보기

14/21

LCS (Longest Common Substring, 최장 공통 부분 수열)

어느 한 문자열 X를 ACDAB라고 한다면, 부분 수열은 {A}, {C}, {D}, {A}, {B}, {A, C}, {A, C, D} … {A, C, D, A, B}가 된다.

LCS는 두 문자열을 비교할 때, 공통 수열 중 길이가 가장 긴 부분 수열을 의미한다.

LCS를 바라보는 방법

기본적으로 DP는 작은 문제의 결과값을 통해서 결국 큰 문제를 해결하는 방식이다.

LCS는 끝 문자 비교를 통해서 더 작은 문자열을 비교하는 케이스로 문제를 작게 만든다.

끝 문자를 비교할 때는 두가지 경우의 수가 발생한다.

1. 끝 문자가 같은 경우

X : BDCAB

Y : ABCBDB

지금 상태에서 X의 마지막 문자와, Y의 마지막 문자가 일치한다.

문자열 X, Y의 LCS를 비교한다고 할 때 다음과 같이 생각해볼 수 있다.

마지막 문자를 뺀 X, Y 문자열 X’, Y’의 LCS길이와 기존의 X, Y의 LCS길이는 아래와 같이 표현할 수 있다.

LCS(X_i, Y_j) = LCS(X_{i-1}, Y_{j-1}) + 1

이미 같은 문자열 B를 상수 1로 고려하고, B를 뺀 나머지 문자열에 대한 LCS를 구하여 더하면 기존 문자열의 LCS라고 볼 수 있다.

2. 끝 문자열이 다른 경우

X : BDCABA

Y : ABCBDB

두 문자열이 다른 경우에는 1번처럼 두 문자열에서 한 번에 문자를 뺄 수 없다. 그래서 X에서 맨 끝 문자열을 뺀 X’와 Y를 비교한 LCS와 Y’와 X의 LCS를 비교하여 더 큰 경우를 선택하게 된다. 더 큰 경우를 선택하는 이유는 우리가 구하고자 하는 바가 ‘최장 길이의 수열’이기 때문이다. 식으로 표현하면 아래와 같다.

LCS(X_i, Y_j) = MAX( LCS(X_{i-1}, Y_j), LCS(X_i, Y_{j-1}))

3. 문자열 길이가 없는 경우

이 이상 문자 비교가 어렵기 때문에 0을 Return한다.

따라서 위 세가지를 종합하면 아래와 같은 LCS 점화식이 나온다.

LCS(X_i, Y_j) = \left\{ \begin{array}{l} 0 \;if\;i=0, j=0 \\ LCS(X_{i-1}, Y_{j-1}) + 1 \;if\;x_i = y_j \\ MAX( LCS(X_{i-1}, Y_j), LCS(X_i, Y_{j-1}))\;if\;x_i \neq y_j \\ \end{array} \right.

길이 구해보기

LCS를 실제 구할때는 행렬, 2차원 배열을 사용해서 구할 수 있다고 한다.

다음 문자열을 통해서 실제 LCS의 길이를 구해보자.

X = ABCBDAB

Y = BDCABA

각 문자열 X,Y 축에 맞게 나열하고 초기 값을 설정해준다.

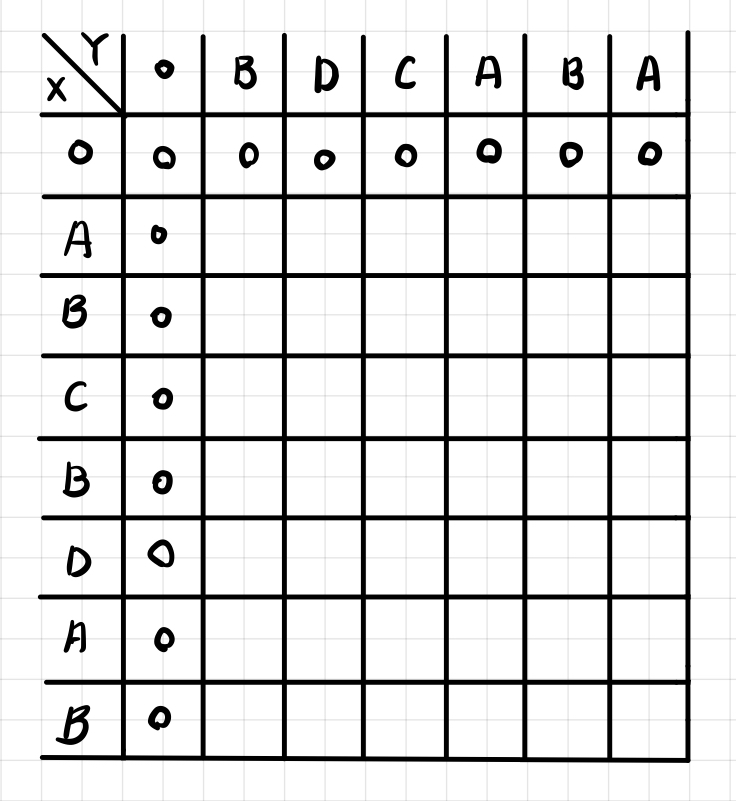
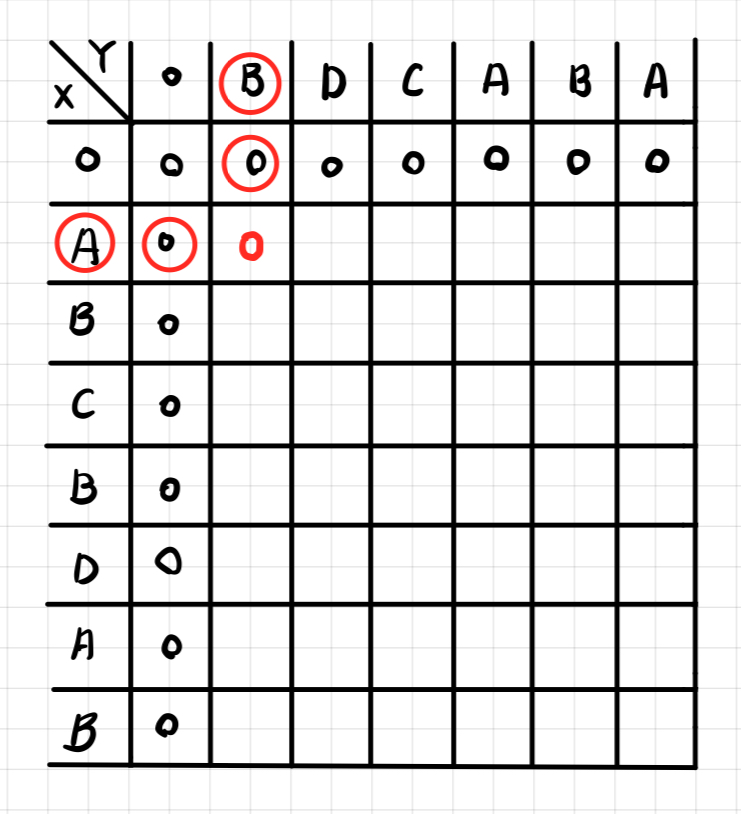
문자가 서로 다른 경우, 점화식에 의해서 [ i - 1, j ]와 [ i, j - 1 ] 값을 비교하여 최대값을 넣는다. 아래 케이스의 경우 두 값이 같기 때문에 0을 넣었다.

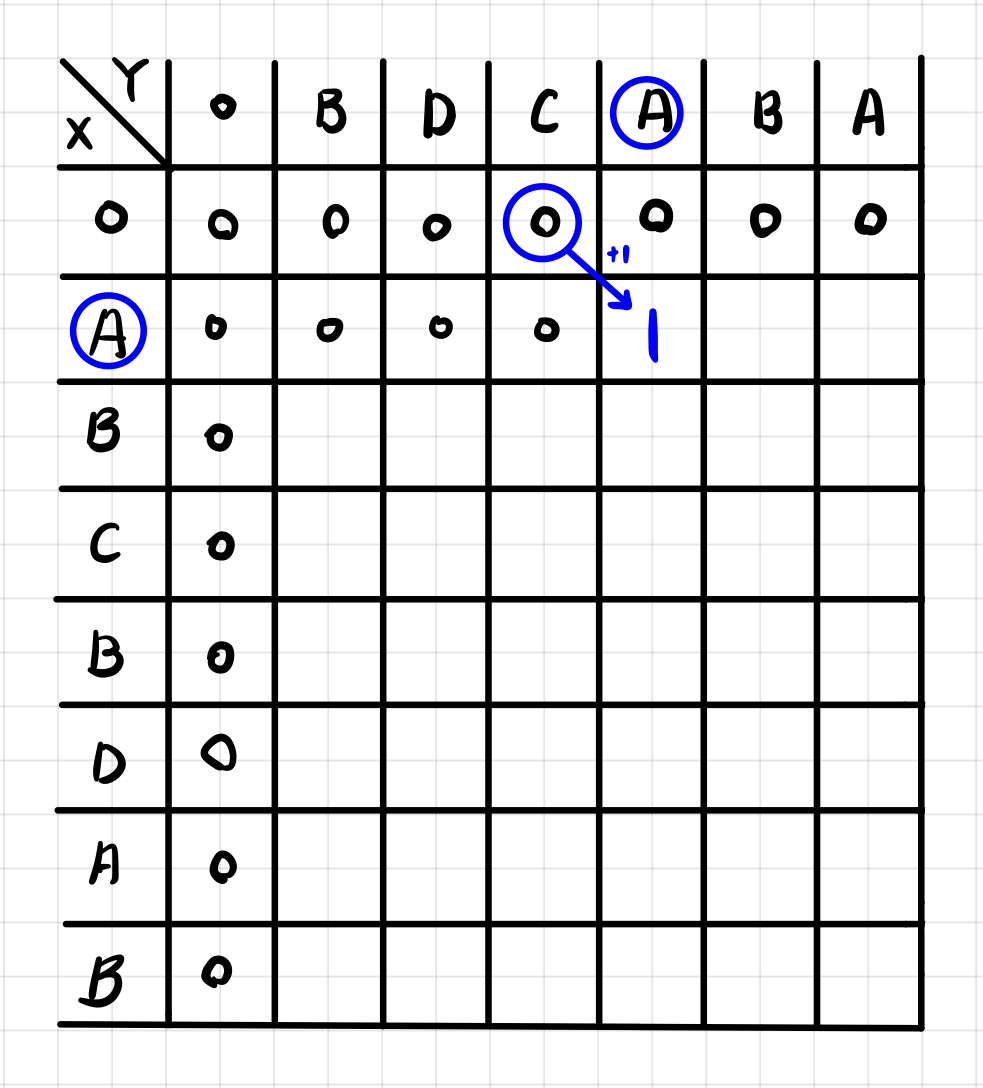
문자가 같은 경우, 점화식에서 [ i - 1, j - 1 ]일 때의 최적 값에 + 1을 해준 값을 넣는다.

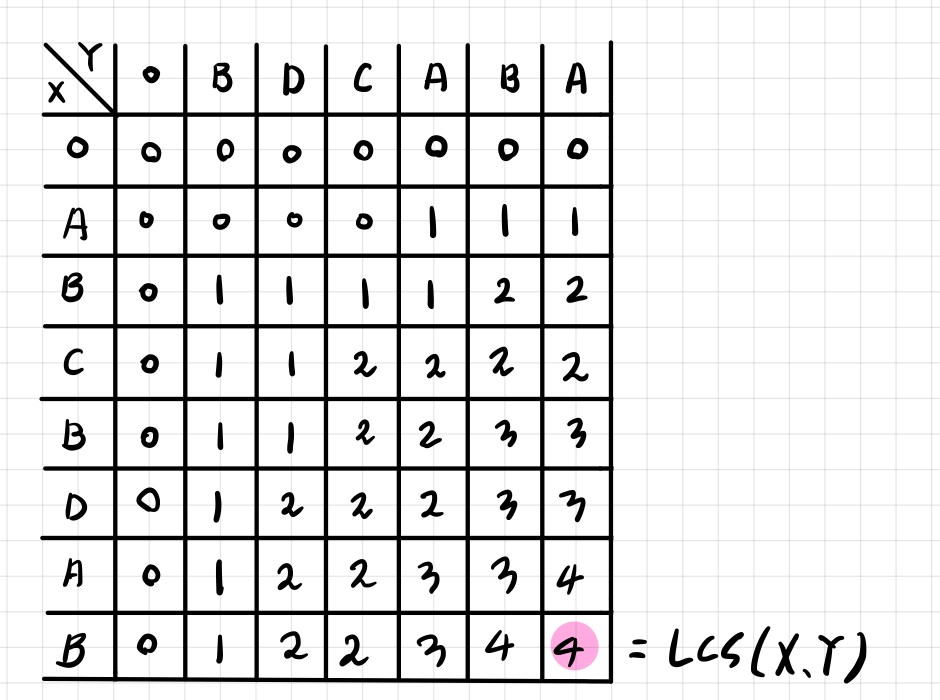
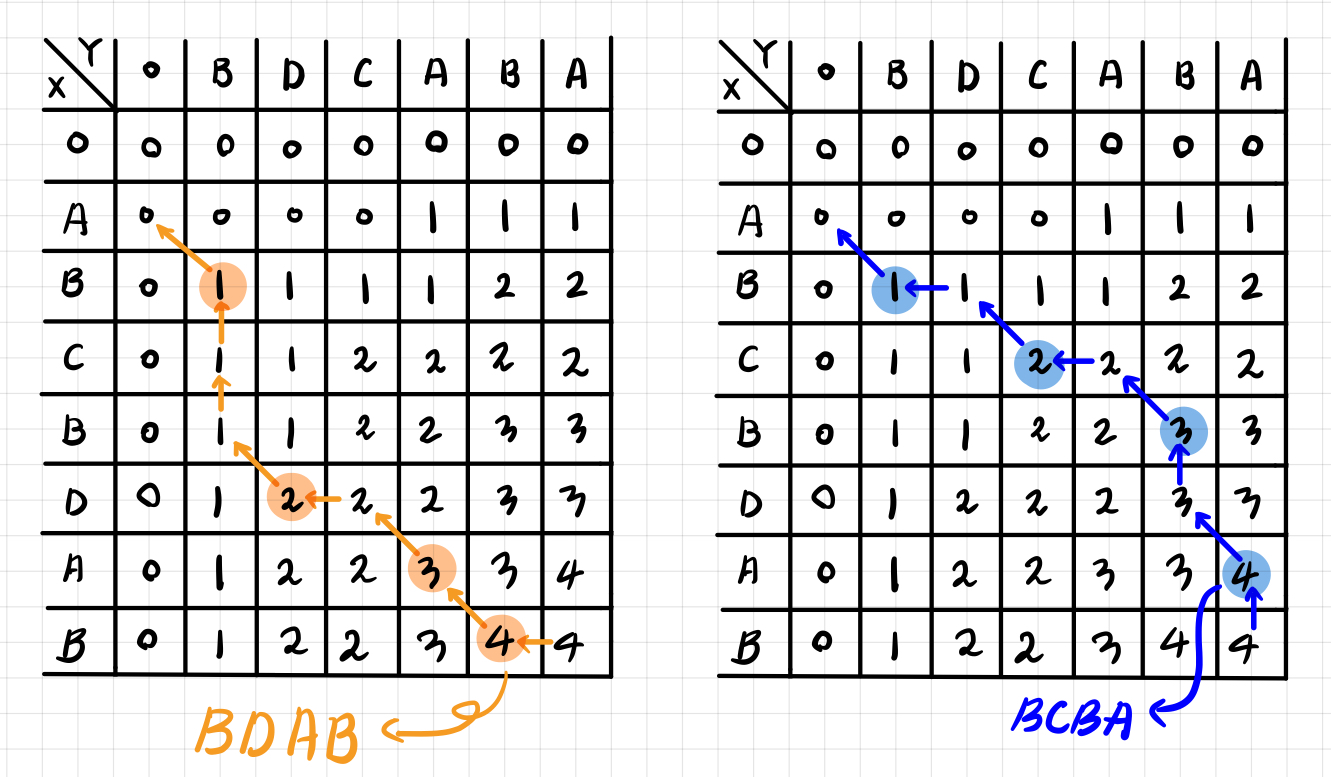
위 두 조건을 반복하며 아래와 같이 테이블을 완성할 수 있다. 그리고 LCS의 길이는 우측 하단의 값이 된다. 이번 예시에서는 LCS의 길이는 4이다.

LCS 문자열 구하기

위 테이블을 활용해서 LCS 문자열이 어떤 문자들로 이루어져 있는지 알 수 있다. 이때 앞서 테이블을 채우기 위해 숫자를 거꾸로 따라가기 때문에 백트래킹 기법이 사용된다고 볼 수 있다.

LCS 길이를 구할 수 있었던 우측하단에서 출발한다. 이때 기준 칸의 위, 아래를 비교하여 경우에 따라 이동하게 된다. 먼저 기준 값과, 왼쪽 값, 위쪽 값이 모두 일치할 경우, 어느 쪽으로 이동해도 상관없다. 이 경우가 의미하는 바는 두 문자열의 LCS는 여러 개가 있을 수 있기 때문에 어느 쪽으로 가느냐에 따라 다른 LCS 문자를 추적하게 된다.

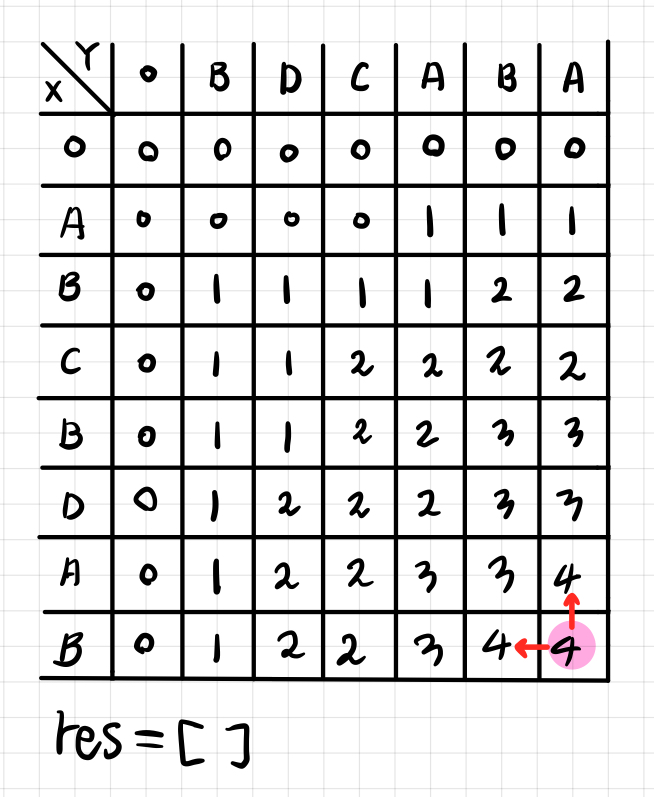- **기준 값의 위쪽 값, 왼쪽 값이 서로 같고 기준 값보다 작은 경우,** 기준 값은 LCS 점화식을 통해 값을 채울 때 [ i - 1, j - 1 ] + 1을 수행한 값이고, 이말인 즉슨, 같은 문자열이었다는 뜻이기 때문에 기준 값에 해당하는 문자를 res 배열에 추가하고 좌측 대각선 상단으로 이동한다.

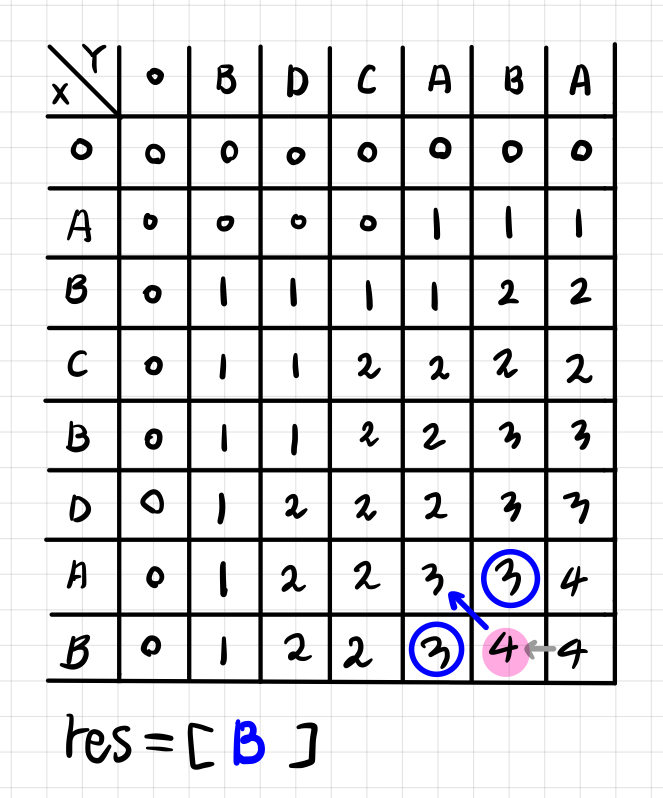
왼쪽 값과 위쪽 값이 서로 다른 경우, 더 큰 쪽으로 이동한다. 이 때는 점화식에서 [ i - 1, j ]와 [ i, j - 1 ]을 비교해서 더 큰 값을 입력한 경우이기 때문에 두 값중 더 큰 값을 통해서 역추적한다.

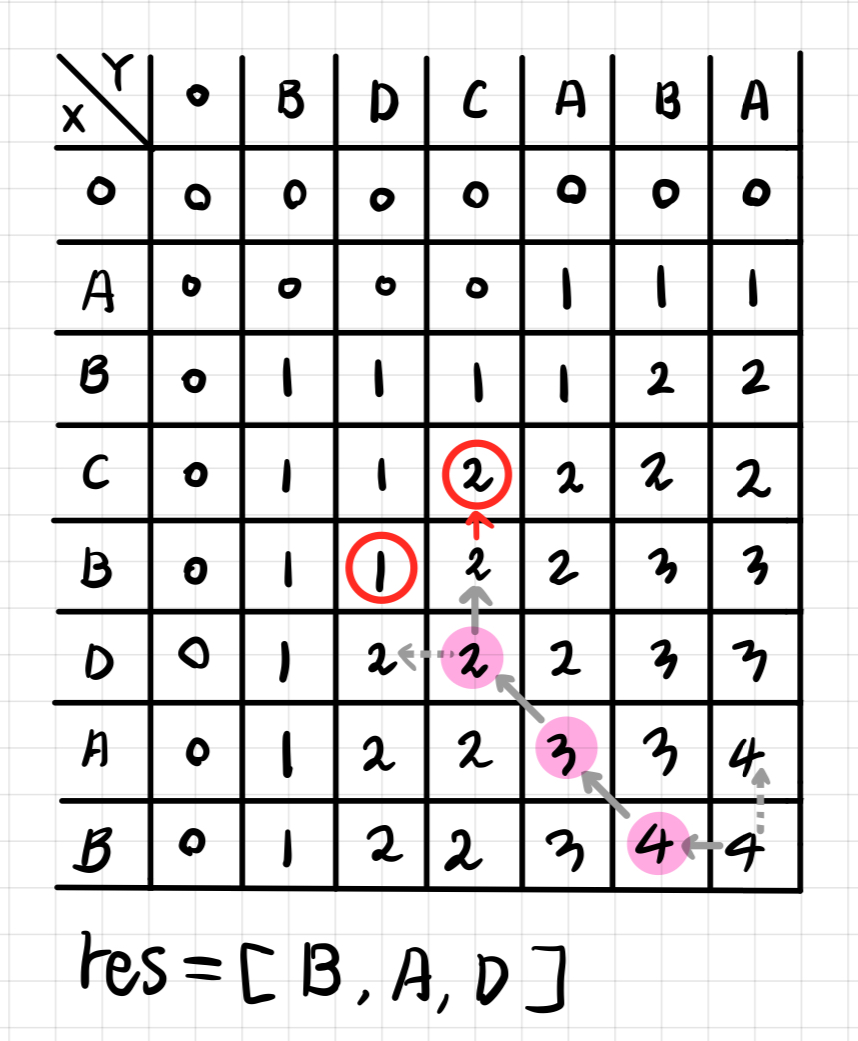
위 규칙을 따라서 이동하면 다음과 같은 루트가 만들어진다. 이때 만들어진 res 배열을 거꾸로 뒤집으면 LCS 문자가 완성된다. 반대로 뒤집는 이유는 우리가 문자열 끝에서 부터 역추적했고, 배열의 뒤로 문자를 넣어줬기 때문에 역순으로 정렬해주어야 올바른 순서가 된다.

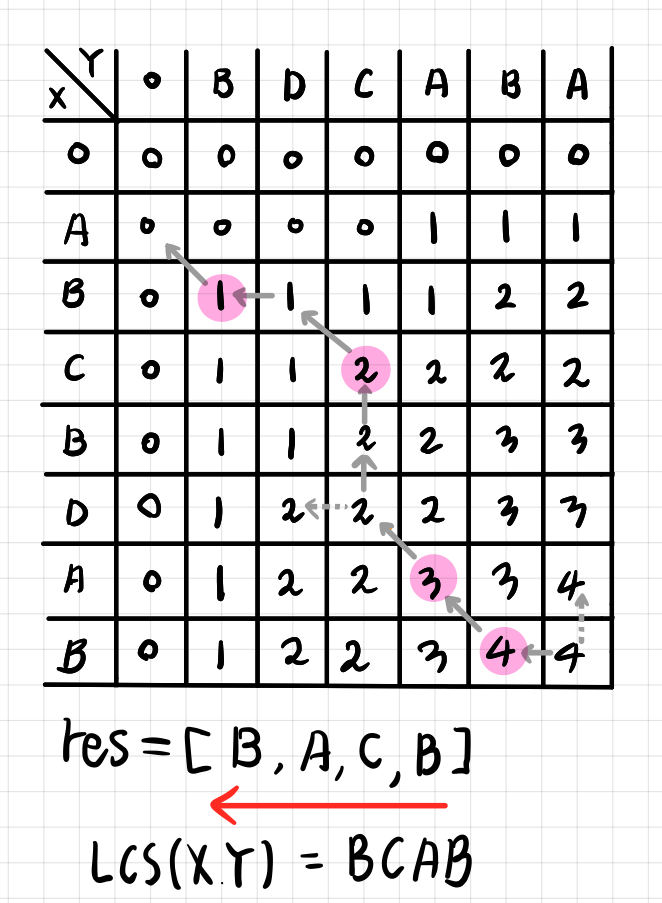
위 방식으로 진행할 수 있는 모든 루트로 백트레킹을 실시하면 모든 LCS 문자열을 구할 수 있다.

코드로 만들어보기

Link: https://www.acmicpc.net/problem/9251

# Bottom-Up
import sys

input = sys.stdin.readline
sys.setrecursionlimit(10**5)

X, Y = [ input()[:-1] for _ in range(2) ]

dp = [ [ 0 ] * ( len(Y) + 1 ) for _ in range( len(X) + 1 ) ]

def LCS(i, j):
  if not dp[i][j]:
    if i == 0 or j == 0:
      return 0
      
    elif X[i - 1] != Y[j - 1]:
      dp[i][j] = max(dp[i-1][j], dp[i][j-1])
      
    else: # X[i] = Y[j] 
      dp[i][j] = dp[i-1][j-1]+ 1
      
  return dp[i][j]

for i in range(1, len(X) + 1):
  for j in range(1, len(Y) + 1):
    LCS(i, j)

print(dp[len(X)][len(Y)])

# Top-Down
import sys

input = sys.stdin.readline
sys.setrecursionlimit(10**5)

X, Y = [ input()[:-1] for _ in range(2) ]

dp = [ [ 0 ] * ( len(Y) + 1 ) for _ in range( len(X) + 1 ) ]

def LCS(i, j):
  if not dp[i][j]:
    if i == 0 or j == 0:
      return 0
      
    elif X[i - 1] != Y[j - 1]:
      dp[i][j] = max(dp[i-1][j], dp[i][j-1])
      
    else: # X[i] = Y[j] 
      dp[i][j] = LCS(i - 1, j - 1) + 1
      
  return dp[i][j]

LCS(len(X), len(Y))

print(dp[len(X)][len(Y)])

그리디 알고리즘 (Greedy Algorithm)

최적해를 구하는데 사용되는 방법 중 하나로, 그 순간 가장 최적이라고 생각하는 방법을 선택해나가는 방식이다.

그리디 알고리즘은 순간 지역적으로 최적의 값을 만들지만 그 값이 누적되었다 해도 그 결과가 최적의 결과라고 보장할 수는 없다.

하지만 그리디 알고리즘을 적용할 수 있는 문제라면 지역적으로 최적의 값들이 전역적으로 최적의 값이 된다.

문제 해결 방법

선택 절차 (Selection Procedure) : 현재 상태에서 최적의 해답을 선택한다.
적절성 검사(Feasibility Check) : 선택된 해가 문제의 조건을 만족하는지 검사한다.
해답 검사(Solution Check) : 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택절차로 다시 돌아가서 과정을 반복한다.

구성요소

그리디 선택 특성 : 전체적인 최적 해를 부분적인 최적 선택에 의해서 만들 수 있다는 특성이다. 어떤 선택을 할지 고려하는 부분에서 결과를 고려할 필요없이 현재 문제에서 최적인 선택을 하면 된다.
최적 부분 구조: 어떤 문제의 최적해가 그 부분 문제에 대한 최적해를 포함하고 있는 특성을 말한다.

그리디 VS 동적 프로그래밍

동적 프로그래밍의 경우 전체 해답이 부분 해에 의존되어있는 상태이다. 그래서 일반적으로 상향식 접근을 통해 작은 문제를 먼저 해결한 후 그 답을 활용하여 전체문제를 해결한다.

그리디 알고리즘은 그 순간 가장 좋은 선택지를 고르고 그에 따라 생기는 부분에 대한 부분 문제를 해결한다. 그래서 미래 선택에 영향을 주지만 미래의 선택이나 부분 문제에 의존하지는 않는다. 하향식 접근을 통해서 주어진 문제를 더 작게 만들어가며 문제를 해결하는 방법으로 문제 해결이 진행된다.

그리디와 동적 프로그래밍 모두 모든 케이스를 통해서 최적의 해를 찾는 방법이다. 다만 접근 방식이 다르다. 그리디는 순간의 최적 값을 추가하기 위해 모든 케이스를 특정 조건으로 정렬하여 케이스를 하나씩 확인하며 문제가 해결되는지 확인한다. 그리고 동적 프로그래밍은 큰 조건의 부분 조건을 먼저 해결하여 그 값을 사용함으로서 반복되는 연산을 줄여 전체 케이스를 탐색하는 시간과 속도를 최적화한 방법으로 볼 수 있다.