pip install PyWavelets
import numpy as np
import pywt
fs = 100
t = np.arange(0, 3, 1 / fs)
f1 = 35
f2 = 10
signal = 0.6 * np.sin(2 * np.pi * f1 * t) + 3 * np.cos(2 * np.pi * f2 * t + np.pi/2)
fft = np.fft.fft(signal) / len(signal)
fft_magnitude = abs(fft)푸리에 변환
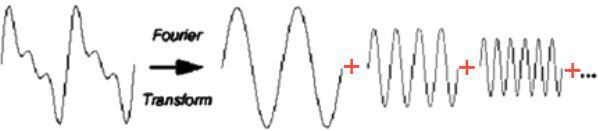
푸리에 변환은 시간에 대한 함수 또는 신호를 주파수 성분으로 분해하는 작업이다. 푸리에 변환은 어떠한 형태의 신호든 다양한 주파수와 크기를 가진 사인 곡선들을 합해서 표현할 수 있다고 가정한다.
그림과 같이 여러 개의 사인 곡선으로 분해한 다음 그 사인 곡선들의 주파수들을 통해 신호 내의 어떤 주파수들이 존재하는지를 알아낼 수 있다.
푸리에 변환은 신호 내에 존재하는 주파수를 분석할 수 있다는 장점이 있지만, 시간에 대한 정보가 사라져서 각 주파수가 시간적으로 언제 존재하는 것인지 알 수 없다는 한계가 있다.
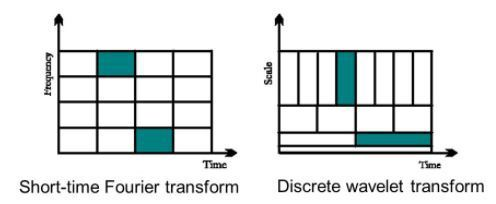
단시간 푸리에 변환(short-time fourier transfrom, STFT)
이러한 한계를 넘어서기 위해 제안된 방법으로 시간에 따라 변화하는 긴 신호를 짧은 시간 단위로 분할한 다음 푸리에 변환을 적용하는 것이다.
결과적으로 각 '시간' 구간마다 어떤 주파수들이 존재하고 있는지 알 수 있으며 비교적 긴 시간 단위로 신호를 분할하면 어떤 '주파수'가 그 시간 내에 존재하는가를 알 수 있다.
즉 window의 너비가 작아질수록 시간분해능이 좋아지고 너비가 커질수록 주파수분해능이 좋아진다.
웨이블릿 변환
주파수분해능과 시간분해능 동시에 좋아지기 위해 웨이블릿 변환이 있다.
웨이블릿 변환은 고주파 성분의 신호에 대해서는 시간 해상도를 높이고 주파수 해상도를 낮춘다. 한편 저주파 성분의 신호에 대해서는 주파수 해상도를 높이고 시간해상도를 낮춘다. SFTF가 시간 분해능과 주파수 분해능 중 하나를 포기해야 했다면, 웨이블릿은 둘 다 잡는다.
시간적으로 무한한 사인곡선을 기본함수로 사용하는 푸리에 변환과 달리, 웨이블릿 변환은 시간적으로 한정되어 있는 웨이블릿 함수를 기본 함수로 사용한다. 웨이블릿은 여러 종류가 있어서 응용분야에 따라 하나를 선택해서 사용하면 된다는 유연성이 있다.
스케일이 작을 때 여러 구간으로 신호를 분리해서 분석하기 때문에 시간 분해능이 좋은 것이고, 스케일이 클 때 신호가 큼직하게 분리되지만 주파수에 대한 정보는 좀 더 잘 살펴볼 수 있기 때문에 주파수 분해능이 좋은 것이다.
결과적으로 웨이블릿 변환은 신호를 근사값(approximation)과 세부값(detail)로 분해한다. 근사값은 신호의 저주파 성분(전반적 내용)을 담고, 세부값은 신호의 고주파 성분(세부 사항)을 담는다.
pywt.families()
>>>['haar',
'db',
'sym',
'coif',
'bior',
'rbio',
'dmey',
'gaus',
'mexh',
'morl',
'cgau',
'shan',
'fbsp',
'cmor']
w = pywt.Wavelet('Haar')
phi, psi, x = w.wavefun(level=10)